Сумма углов n-угольника

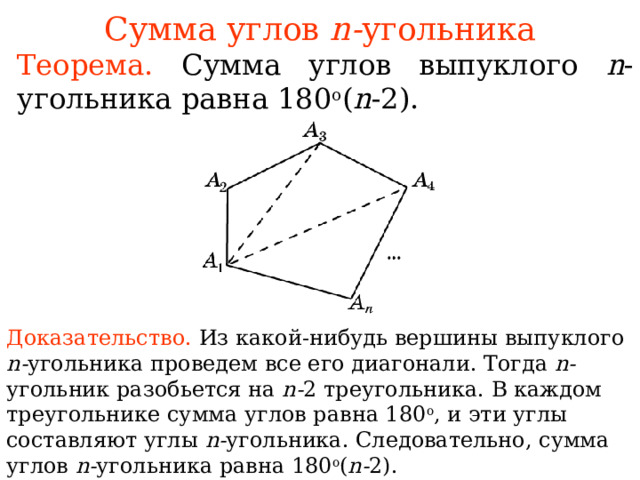
Сумма углов n- угольника

Теорема. Сумма углов выпуклого n -угольника равна 180 o ( n -2).

В режиме слайдов ответы появляются после кликанья мышкой

Доказательство. Из какой-нибудь вершины выпуклого n- угольника проведем все его диагонали. Тогда n- угольник разобьется на n - 2 треугольника. В каждом треугольнике сумма углов равна 180 о , и эти углы составляют углы n- угольника. Следовательно, сумма углов n- угольника равна 180 о ( n - 2).

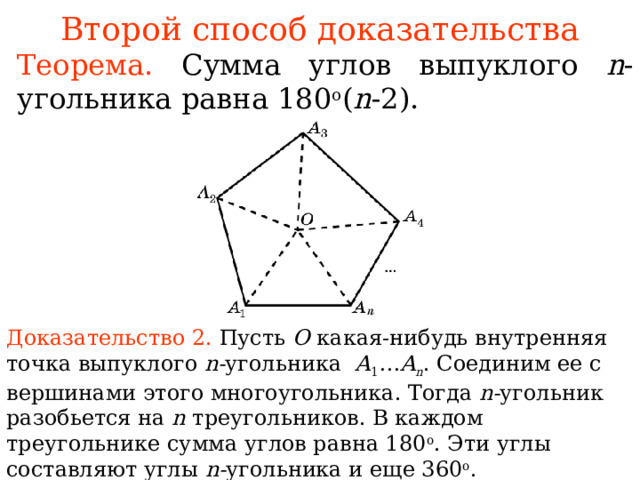
Второй способ доказательства

Теорема. Сумма углов выпуклого n -угольника равна 180 o ( n -2).

В режиме слайдов ответы появляются после кликанья мышкой

Доказательство 2 . Пусть O как ая -нибудь внутренняя точка выпуклого n- угольника A 1 … A n . Соединим ее с вершинами этого многоугольника . Тогда n- угольник разобьется на n треугольник ов . В каждом треугольнике сумма углов равна 180 о . Э ти углы составляют углы n- угольника и еще 360 о . Следовательно, сумма углов n- угольника равна 180 о ( n - 2).

Упражнение 1

Чему равна сумма углов выпуклого: а) 4-угольника; б) 5-угольника; в) 6-угольника?

Ответ: а) 360 о ;

б) 540 о ;

в) 720 о .

В режиме слайдов ответы появляются после кликанья мышкой

Упражнение 2

Чему равен внешний угол правильного: а) 3-угольника; б) 4-угольника; в) 5-угольника; г) 6-угольника?

Ответ: а) 120 о ;

б) 90 о ;

в) 72 о ;

В режиме слайдов ответы появляются после кликанья мышкой

г) 60 о .

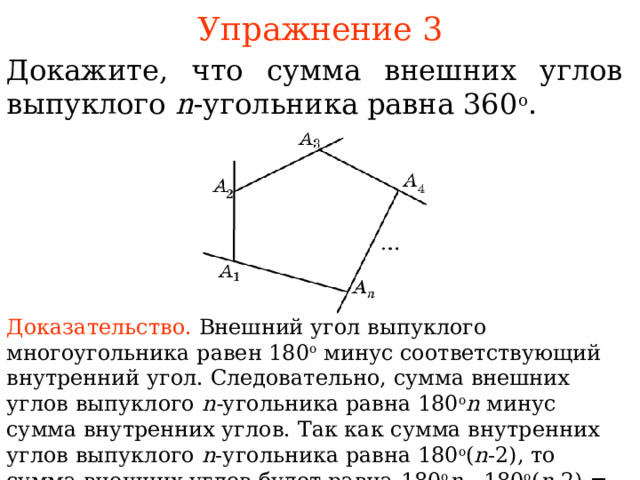
Упражнение 3

Докажите, что сумма внешних углов выпуклого n -угольника равна 360 о .

В режиме слайдов ответы появляются после кликанья мышкой

Доказательство. Внешний угол выпуклого многоугольника равен 180 о минус соответствующий внутренний угол. Следовательно, сумма внешних углов выпуклого n - угольника равна 180 о n минус сумма внутренних углов. Так как сумма внутренних углов выпуклого n -угольника равна 180 о ( n -2), то сумма внешних углов будет равна 180 о n - 180 о ( n -2) = 360 о .

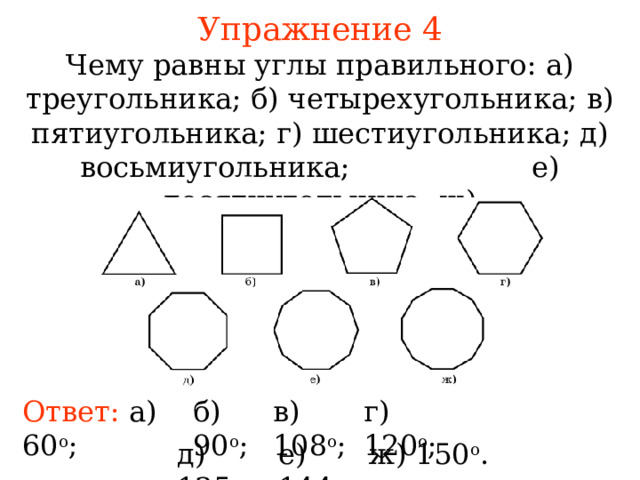
Упражнение 4

Чему равны углы правильного: а) треугольника; б) четырехугольника; в) пятиугольника; г) шестиугольника ; д) восьмиугольника; е) десятиугольника; ж) двенадцатиугольника ?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: а) 60 о ;

б) 90 о ;

в) 108 о ;

г) 120 о ;

д) 135 о ;

е) 144 о ;

ж) 150 о .

Упражнение 5

Сумма трех углов выпуклого четырехугольника равна 300 о . Найдите четвертый угол.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 60 о .

Упражнение 6

Углы выпуклого четырехугольника пропорциональны числам 1, 2, 3, 4. Найдите их.

Ответ: 36 о , 72 о , 108 o , 144 o .

В режиме слайдов ответы появляются после кликанья мышкой

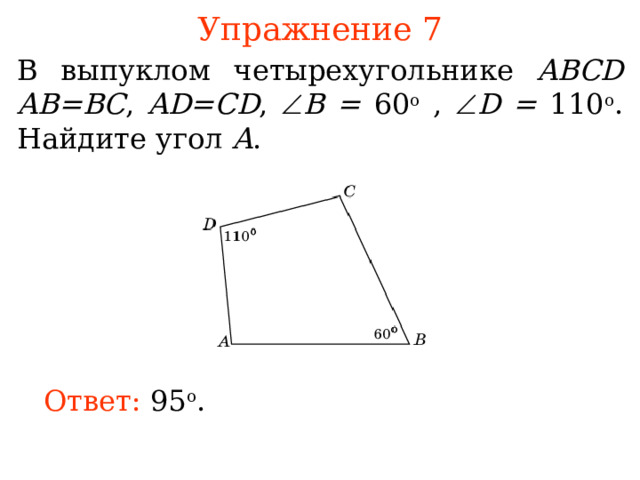
Упражнение 7

В выпуклом четырехугольнике ABCD AB = BC , AD = CD ,  B = 60 о ,  D = 110 о . Найдите угол A .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 95 о .

Упражнение 8

Сумма углов выпуклого многоугольника равна 900 o . Сколько у него сторон?

Ответ: 7.

В режиме слайдов ответы появляются после кликанья мышкой

Упражнение 9

Сколько сторон имеет правильный многоугольник, если каждый из его внешних углов равен: а) 36 o ; б) 24 o ?

Ответ: а) 10;

В режиме слайдов ответы появляются после кликанья мышкой

б) 15 .

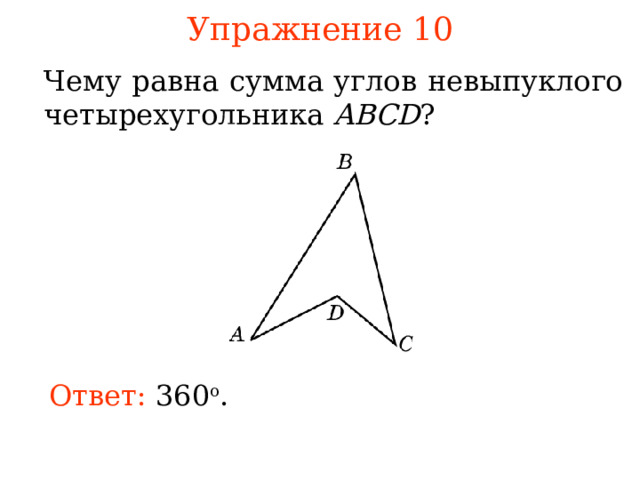
Упражнение 1 0

Чему равна сумма углов невыпуклого четырехугольника ABCD ?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 360 о .

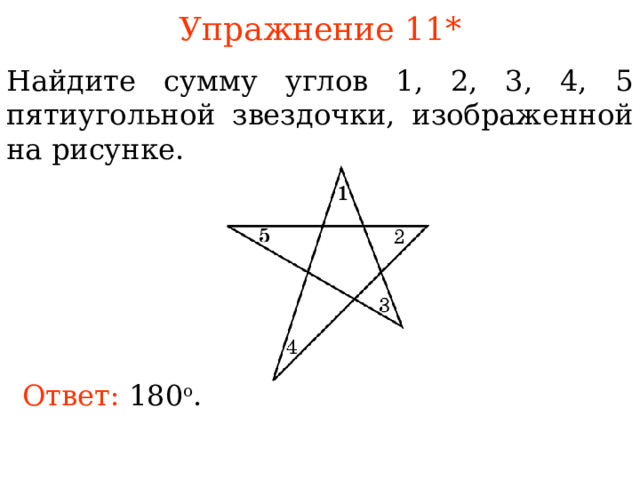
Упражнение 1 1*

Найдите сумму углов 1, 2, 3, 4, 5 пятиугольной звездочки, изображенной на рисунке.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 180 о .

Упражнение 1 2*

Какое наибольшее число острых углов может иметь выпуклый n -угольник?

Решение. Так как сумма внешних углов выпуклого многоугольника равны 360 о , то у выпуклого многоугольника не может быть более трех тупых углов, следовательно, у него не может быть более трех внутренних острых углов.

Ответ. 3.

В режиме слайдов ответы появляются после кликанья мышкой