Сумма углов треугольника

Тема урока: «Сумма углов треугольника».

«Величие человека – в его способности мыслить». Б.Паскаль

Цель урока:

Выяснить:

- Чему равна сумма углов любого треугольника.

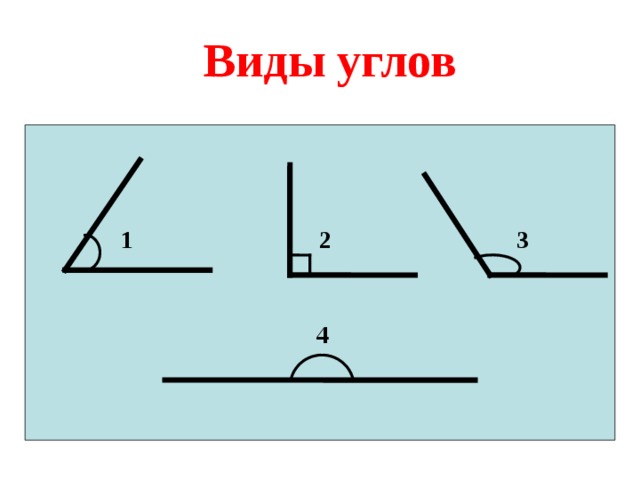
Виды углов

1

2

3

4

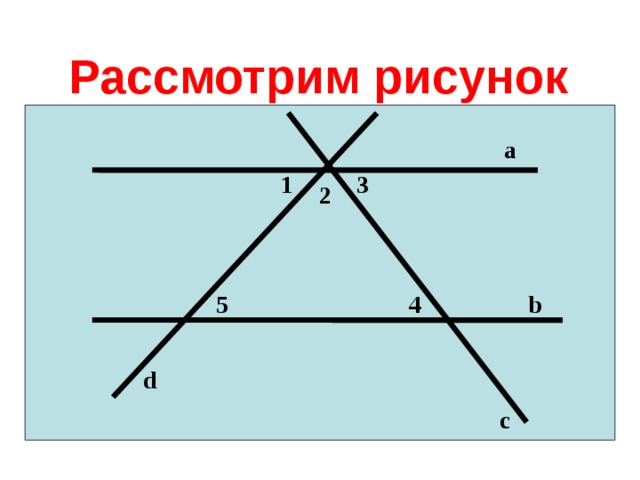
Рассмотрим рисунок

а

1

3

2

b

4

5

d

с

Лабораторная работа.

Указание к работе

1. Постройте в тетради произвольный треугольник АВС.

2. Измерьте градусные меры углов треугольника.

3.Запишите в тетрадь:

 А =…,  В =…,  С=…

4. Найдите сумму углов треугольника

 А +  В +  С=…

5.Сравните полученные результаты.

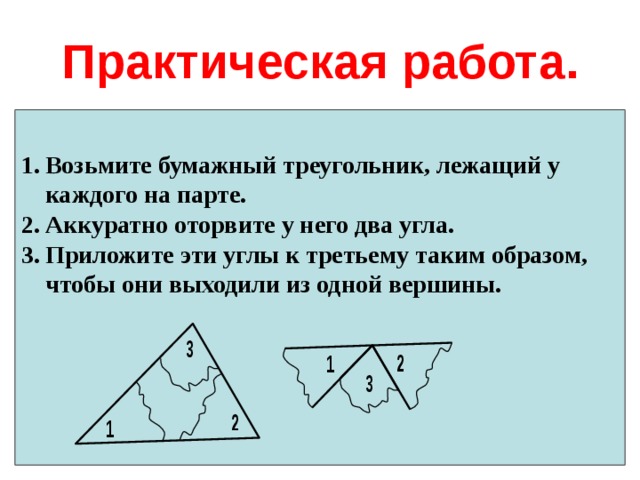
Практическая работа.

• Возьмите бумажный треугольник, лежащий у каждого на парте.
• Аккуратно оторвите у него два угла.
• Приложите эти углы к третьему таким образом, чтобы они выходили из одной вершины.

Теорема

Сумма углов треугольника равна

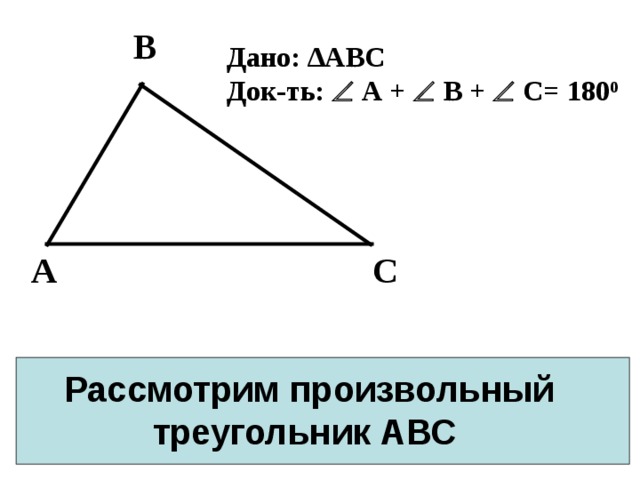
В

Дано: ∆АВС

Док-ть:  А +  В +  С= 180 0

С

А

Рассмотрим произвольный треугольник АВС

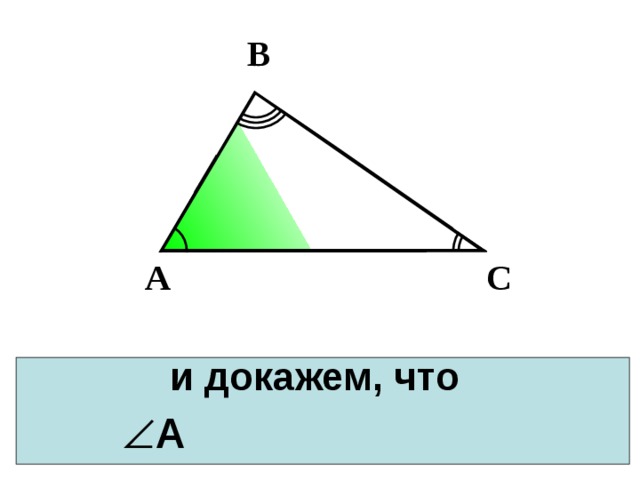
В

С

А

и докажем, что

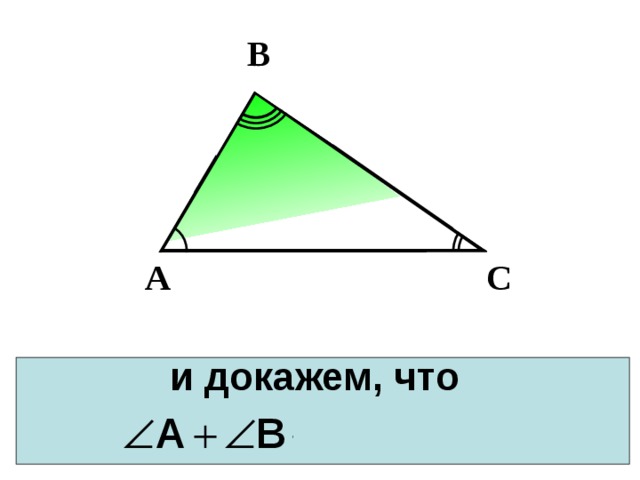
В

С

А

и докажем, что

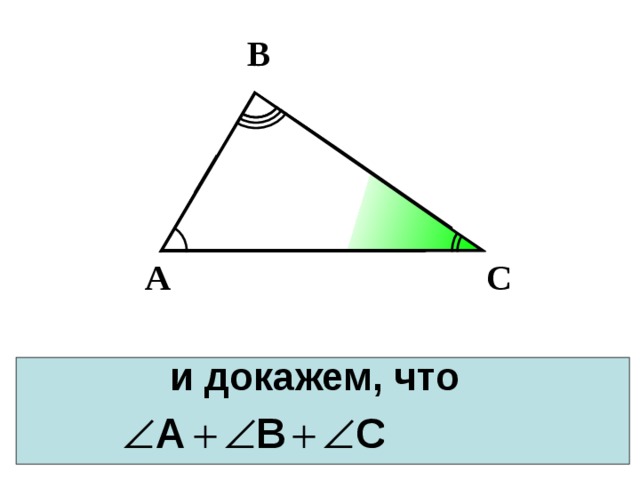
В

С

А

и докажем, что

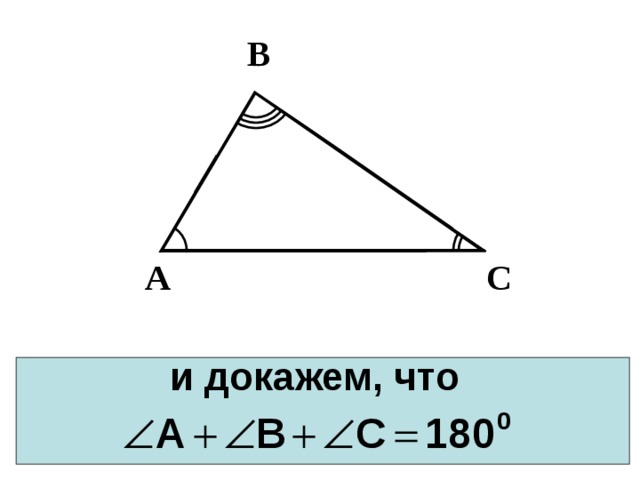
В

С

А

и докажем, что

В

С

А

С

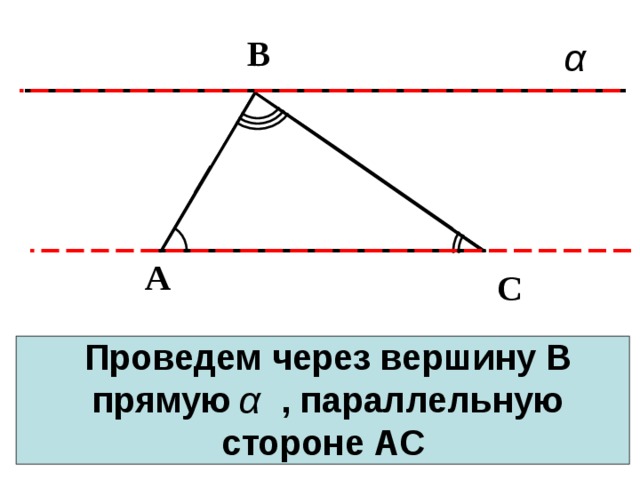
Проведем через вершину В прямую , параллельную стороне АС

В

4

1

С

А

С

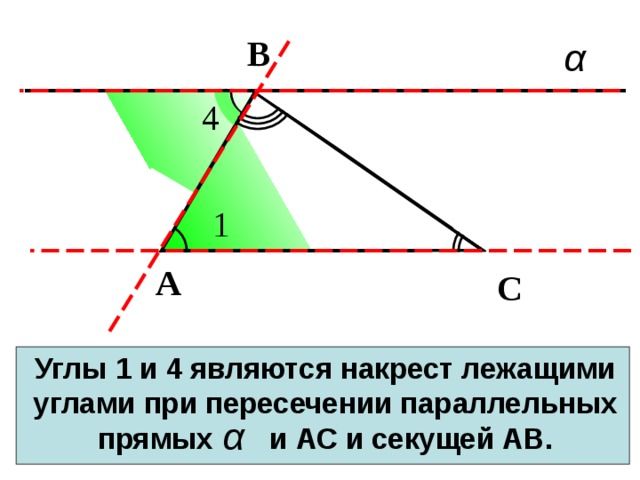
Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых и АС и секущей АВ.

В

5

3

С

А

С

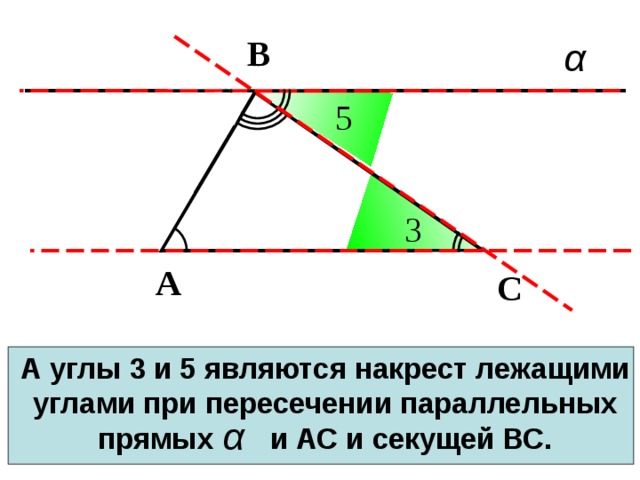
А углы 3 и 5 являются накрест лежащими углами при пересечении параллельных прямых и АС и секущей ВС.

В

5

4

3

1

С

А

С

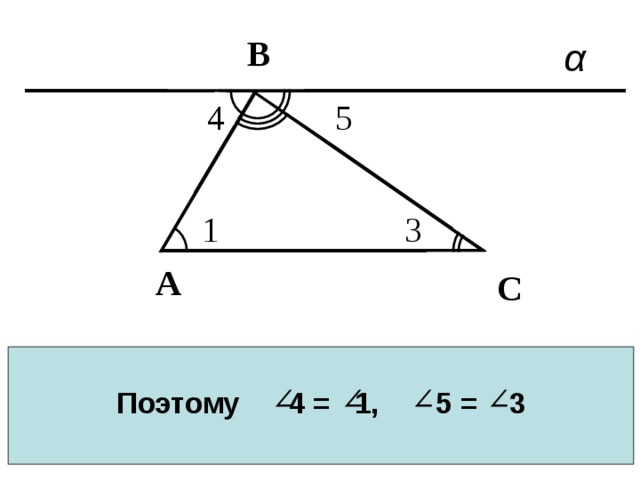
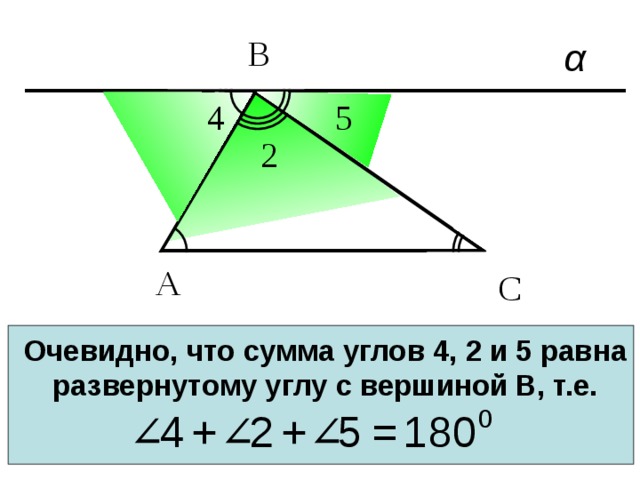
Поэтому 4 = 1, 5 = 3

В

4

5

2

С

А

С

Очевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т.е.

В

4

5

2

1

3

С

А

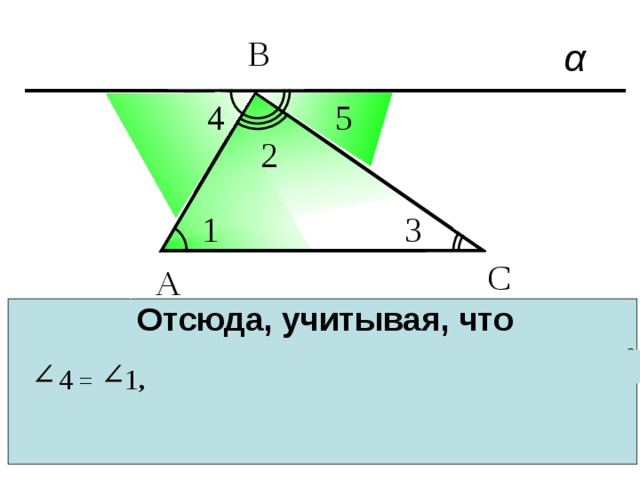
Отсюда, учитывая, что получаем или

4 = 1 ,

В

5

4

2

3

1

С

А

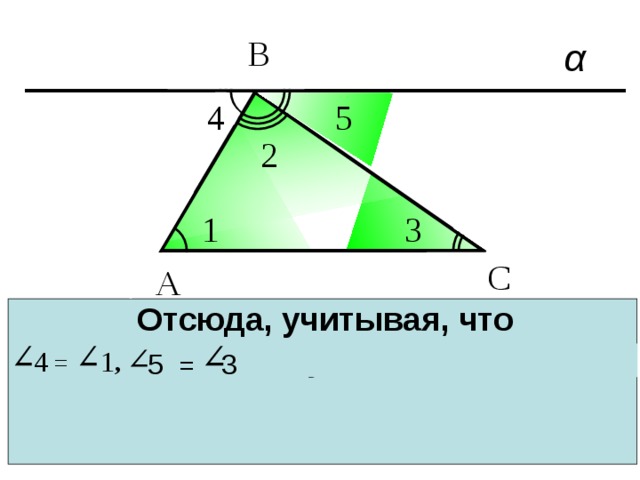
Отсюда, учитывая, что получаем или

4 = 1 ,

5 = 3

Примерный план доказательства

Историческая справка

Доказательство данного факта, изложенное в современных учебниках, содержалось ещё в комментарии к «Началам» Евклида древнегреческого учёного Прокла ( V в.н.э.) Прокл утверждает, что согласно Евдему Родосскому, это доказательство было открыто ещё пифагорейцами

( V в.до н.э.).

Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.

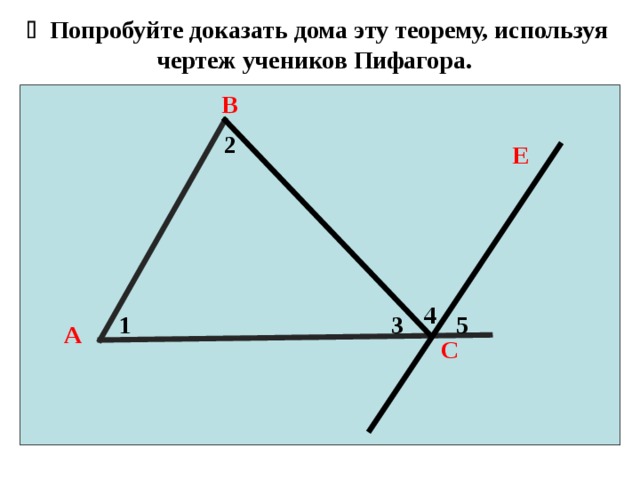
 Попробуйте доказать дома эту теорему, используя чертеж учеников Пифагора.

В

2

Е

4

1

3

5

А

С

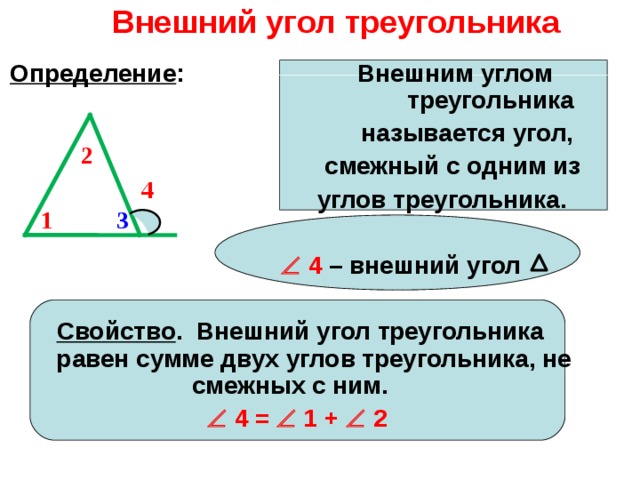
Внешний угол треугольника

Определение : Внешним углом треугольника

называется угол,

смежный с одним из

углов треугольника.  

 4 – внешний угол

Свойство .  Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

   4 =  1 +  2

2

4

1

3

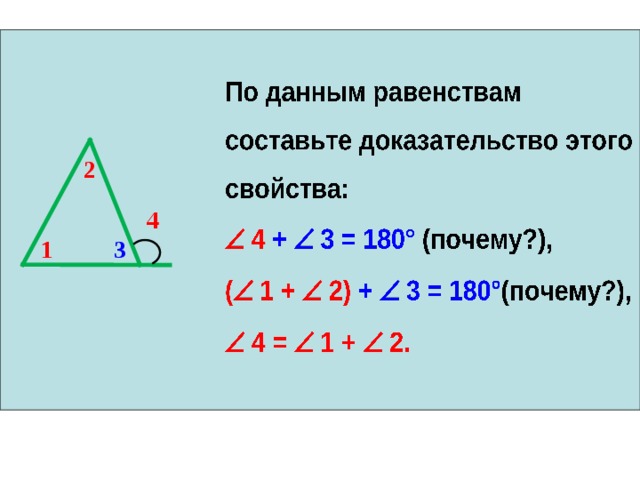
2

4

1

3

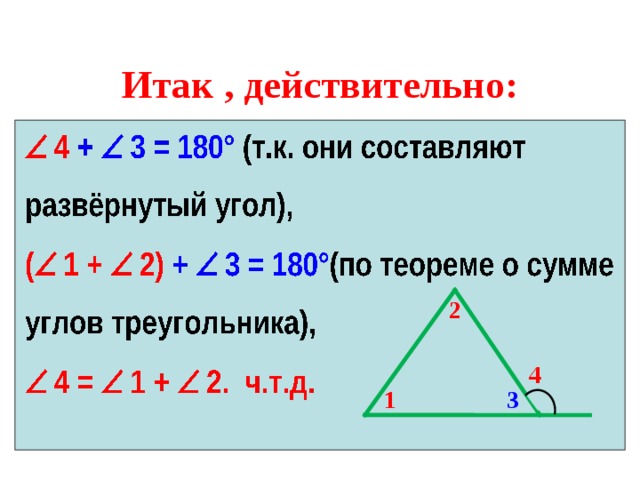
Итак , действительно:

2

4

1

3

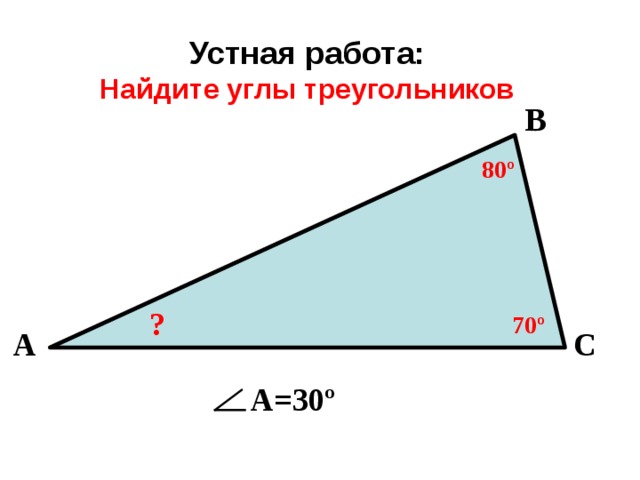
Устная работа: Найдите углы треугольников

В

80 º

?

70 º

А

С

А=30 º

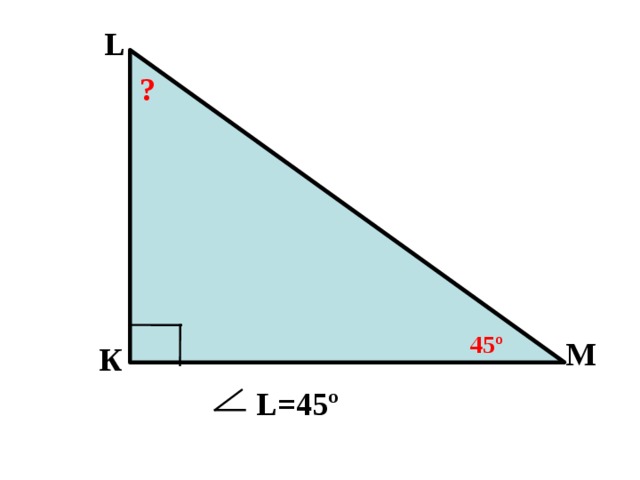
L

?

45 º

M

К

L =45 º

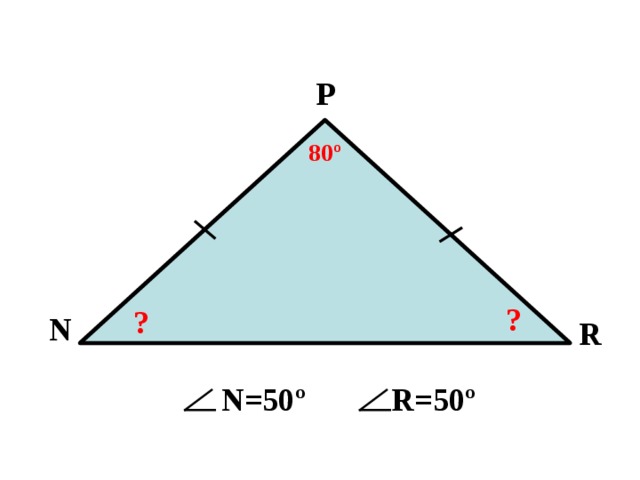
P

80 º

?

?

N

R

N =50 º

R =50 º

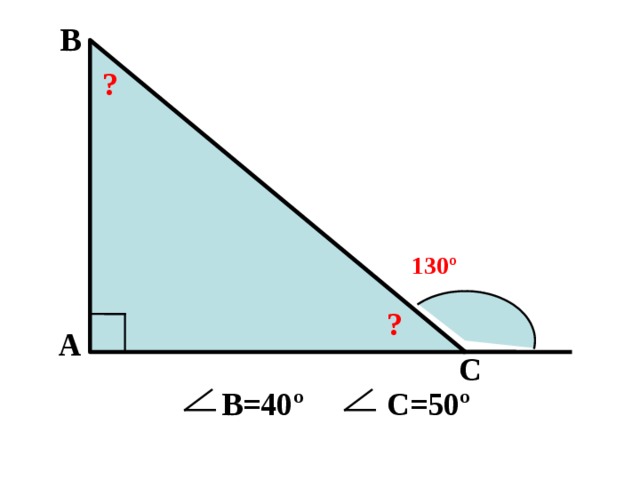
В

?

130 º

?

А

С

В=40 º

С=50 º

Существует ли треугольник с углами:

а) 30˚, 60˚, 90˚ б) 46˚, 160˚, 4˚

в) 75˚, 80˚, 25˚ г) 100˚, 20˚, 55˚

Работа с учебником.

Стр.71 №223 а)

№ 228 а)

Практическое применение знаний. Свойство углов прямоугольного равнобедренного треугольника знал еще один из первых творцов геометрической науки древнегреческий ученый Фалес. Используя его, он измерял высоту египетской пирамиды по длине ее тени. По легенде, Фалес выбрал день и время, когда длина его собственной тени равнялась его росту, поскольку в этот момент высота пирамиды также должна равняться длине тени, которую она отбрасывает. Конечно, длину тени можно было вычислить от средней точки квадратной основы пирамиды, но ширину основы Фалес мог измерять непосредственно. Таким образом, можно измерять высоту любого дерева.

Итог урока. Сегодня на уроке мы доказали исследовательским путем теорему о сумме углов треугольника, научились применять приобретенные знания в практической деятельности. Мы еще раз убедились, что геометрия это наука, которая возникла из потребностей человека. Ведь, как писал Галилей: “Природа разговаривает языком математики: буквы этого языка - окружности, треугольники и прочие математические фигуры».  

Домашнее задание

• П.30, №223(б), №228(в).
• Другой способ доказательства теоремы о сумме углов треугольника.

Спасибо за внимание!