Суммативное оценивание за раздел «Алгебраические выражения»
Тема Переменная. Выражение с переменной Раскрытие скобок. Коэффициент. Подобные слагаемые. Приведение подобных слагаемых Тождественные преобразования выражений. Тождество Преобразования алгебраических выражений Решение текстовых задач
Цель обучения 6.2.1.3 находить допустимые значения переменной в алгебраическом выражении
6.2.1.5 знать правила раскрытия скобок
6.2.1.7 приводить подобные слагаемые в алгебраических выражениях
6.2.1.9 выполнять тождественные преобразования алгебраических выражений
6.5.2.4 составлять выражения с переменными и формулы при решении текстовых задач
Критерий оценивания Обучающийся
• Находит допустимые значения переменной в алгебраическом выражении
• Раскрывает скобки и приводит подобные слагаемые в алгебраических выражениях
• Доказывает тождество, с помощью преобразования алгебраических выражений • Составляет выражения с переменными при решении текстовых задач
Уровень мыслительных навыков Применение Навыки высокого порядка
Время выполнения 25 минут
1 вариант
1. При каких значениях переменных имеет смысл выражение: а) 4х - 6; b) [2]
[2]
2. Упростите выражение:  [3]
[3]
3. Докажите тождество: (4а – 12)∙0,6 – 0,9∙(3а – 5) – (– 0,6 – 0,3а) = - 2,1. [3]
4. Расстояние между двумя пристанями теплоход проходит по течению реки за 2 ч, а против течения - за 2,8 ч. Собственная скорость теплохода а км/ч, а скорость течения реки b км/ч. Составьте выражение по условию задачи для нахождения:
а) Скорости теплохода по течению и против течения реки?
b) Расстояния, пройденного теплоходом по течению реки?
c) Расстояния, пройденного теплоходом против течения реки?
d) Общего расстояния, пройденного теплоходом по течению реки и против течения реки.
е) Используя выражение из пункта (d), найдите его значение при а = 27 км/ч и b = 3 км/ч. [6]
2 вариант
1. При каких значениях переменных имеет смысл выражение: а) 7х - 8; b) [2]
[2]
2. Упростите выражение: 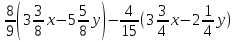 [3]
[3]
3. Докажите тождество: (5а – 9)∙0,8 – 1,4∙(3а – 4) – (– 1,3 – 0,2a) = - 0,3. [3]
4. Расстояние между двумя пристанями теплоход проходит по течению реки за 4 ч, а против течения – за 4,4 ч. Собственная скорость теплохода m км/ч, а скорость течения реки n км/ч. Составьте выражение по условию задачи для нахождения:
а) Скорости теплохода по течению и против течения реки?
b) Расстояния, пройденного теплоходом по течению реки?
c) Расстояния, пройденного теплоходом против течения реки?
d) Общего расстояния, пройденного теплоходом по течению реки и против течения реки.
е) Используя выражение из пункта (d), найдите его значение при m = 28 км/ч и n = 4 км/ч. [6]
Тема Переменная. Выражение с переменной Раскрытие скобок. Коэффициент. Подобные слагаемые. Приведение подобных слагаемых Тождественные преобразования выражений. Тождество Преобразования алгебраических выражений Решение текстовых задач
Цель обучения 6.2.1.3 находить допустимые значения переменной в алгебраическом выражении
6.2.1.5 знать правила раскрытия скобок
6.2.1.7 приводить подобные слагаемые в алгебраических выражениях
6.2.1.9 выполнять тождественные преобразования алгебраических выражений
6.5.2.4 составлять выражения с переменными и формулы при решении текстовых задач
Критерий оценивания Обучающийся
• Находит допустимые значения переменной в алгебраическом выражении
• Раскрывает скобки и приводит подобные слагаемые в алгебраических выражениях
• Доказывает тождество, с помощью преобразования алгебраических выражений • Составляет выражения с переменными при решении текстовых задач
Уровень мыслительных навыков Применение Навыки высокого порядка
Время выполнения 25 минут
3 вариант
1. При каких значениях переменных имеет смысл выражение: а) 9х - 6; b)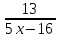 [2]
[2]
2. Упростите выражение: 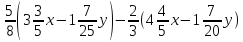 [3]
[3]
3. Докажите тождество: (4а – 13)∙0,3 – 0,8∙(3а – 4) – (– 1,8 – 1,2а) = 1,1. [3]
4. Расстояние между двумя пристанями теплоход проходит по течению реки за 2.2 ч, а против течения - за 3 ч. Собственная скорость теплохода с км/ч, а скорость течения реки d км/ч. Составьте выражение по условию задачи для нахождения:
а) Скорости теплохода по течению и против течения реки?
b) Расстояния, пройденного теплоходом по течению реки?
c) Расстояния, пройденного теплоходом против течения реки?
d) Общего расстояния, пройденного теплоходом по течению реки и против течения реки.
е) Используя выражение из пункта (d), найдите его значение при c = 28 км/ч и d = 4 км/ч. [6]
4 вариант
1. При каких значениях переменных имеет смысл выражение: а) 5х - 7; b)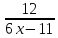 [2]
[2]
2. Упростите выражение:  [3]
[3]
3. Докажите тождество: (3а – 12)∙0,7 – 1,6∙(2а – 4) – (– 1,4 – 1,1a} = - 0,6. [3]
4. Расстояние между двумя пристанями теплоход проходит по течению реки за 2.4 ч, а против течения – за 3,2 ч. Собственная скорость теплохода a км/ч, а скорость течения реки b км/ч. Составьте выражение по условию задачи для нахождения:
а) Скорости теплохода по течению и против течения реки?
b) Расстояния, пройденного теплоходом по течению реки?
c) Расстояния, пройденного теплоходом против течения реки?
d) Общего расстояния, пройденного теплоходом по течению реки и против течения реки.
е) Используя выражение из пункта (d), найдите его значение при a = 33 км/ч и b = 5 км/ч. [6]







 [2]
[2] [3]
[3] [2]
[2]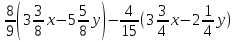 [3]
[3]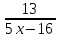 [2]
[2]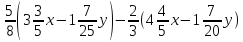 [3]
[3]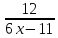 [2]
[2] [3]
[3]









