Россия, Воронеж
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 19.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 19.09.2024 16:38
Петрова Елена Владимировна
Учитель математики, физики, информатики
4 426
12 276 
Местоположение
Специализация
Свойчтва параллельных плоскостей
Категория:
Математика
25.09.2018 19:18
Просмотр содержимого документа
«Свойчтва параллельных плоскостей»
Свойства параллельных плоскостей.
Цели и задачи:
Сформулировать и доказать свойства параллельных плоскостей.
Сформировать навыки применения изученных свойств параллельных плоскостей при решении задач.
Развивать пространственное воображение.
Воспитывать аккуратность при выполнении чертежей.
Ход урока.
Оргмомент.
Актуализации опорных знаний (устный опрос) и проверка домашнего задания.
Дайте определение параллельных плоскостей.
Сформулируйте и докажите признак параллельности двух плоскостей (Слайд 3).
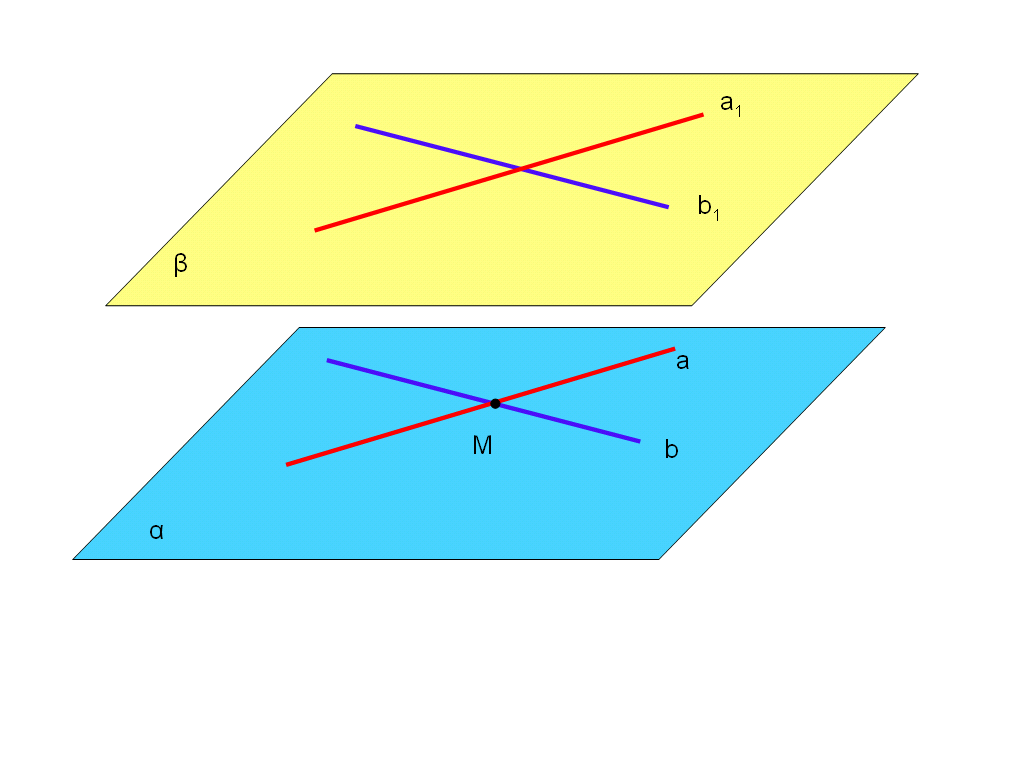
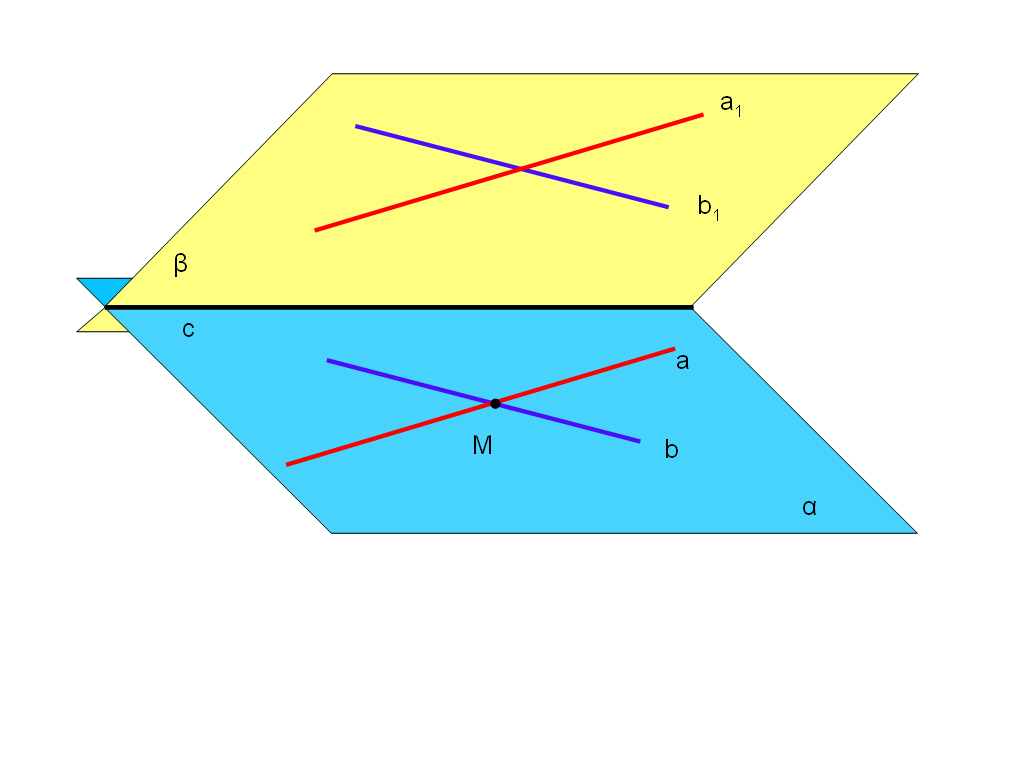
Сформулируйте второй признак параллельности плоскостей (№ 51).
О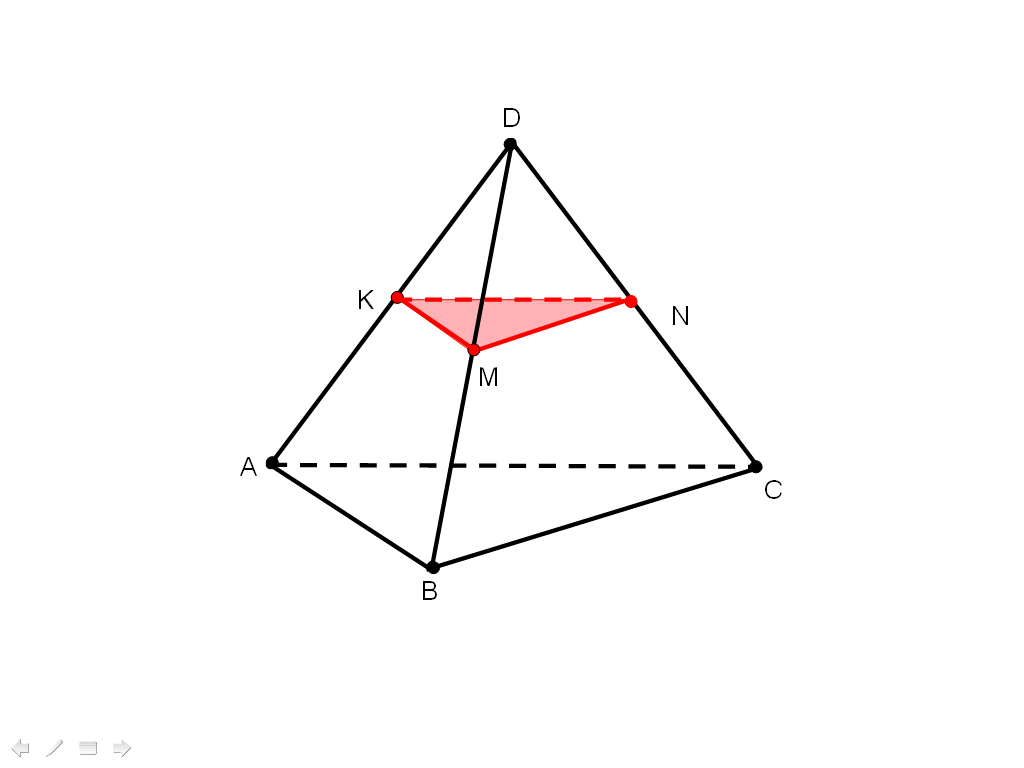
бъяснить решение задачи из домашней работы.
Построить сечение треугольной пирамиды плоскостью, параллельной основанию и проходящей через точку, принадлежащую боковому ребру (Слайд 4)
Объяснение нового материала.
Свойства параллельных плоскостей.
Свойство 1.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Д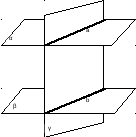
ано: α||β, γ∩α = a, γ∩β = b.
Доказать: a||b
Доказательство: Предположим, что a∩b=M = M
α (так как aα),
M β (так как b β),
то есть α∩β, что противоречит условию. Значит прямые a и b не пересекаются, а так как они лежат в одной плоскости γ, то a||b.
Свойство 2.
О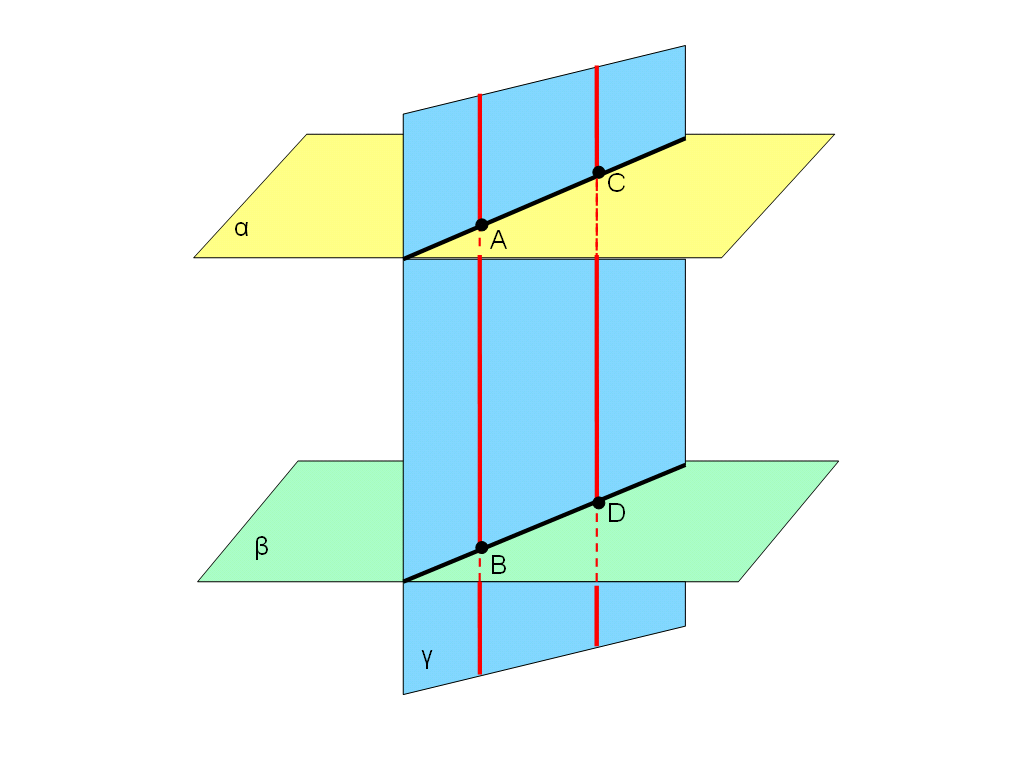
трезки параллельных прямых, заключенные между параллельными плоскостями равны (Слайд 6).
Дано: AB||CD, α||β.
Докажем, что AB=CD.
Плоскость γ, проходящая через параллельные прямые AB и CD, пересекается с плоскостями α и β по параллельным прямым AC и BD (Свойство 1). Следовательно, ABDC – параллелограмм по определению. Но в параллелограмме противоположные стороны равны, поэтому AB=CD.
Закрепление изученных свойств в ходе решения задач.
№ 63(б)
П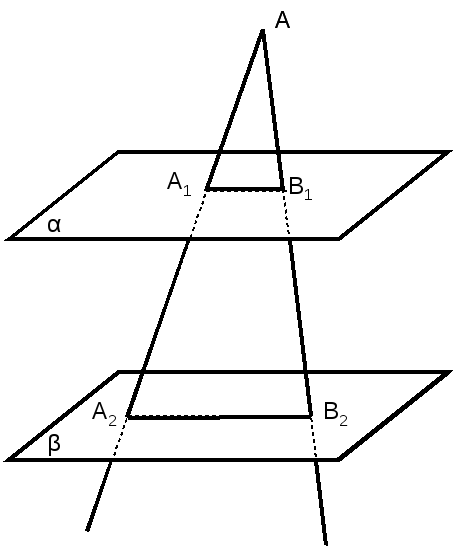
араллельные плоскости α и β пересекают сторону AB угла BAC соответственно в точках A1 и A2, а сторону AC этого угла - соответственно в точках B1 и B2 . Найдите A2B2 и AA2 , если A1B1 равно 18 см, AA1 = 24см, AA2 = 
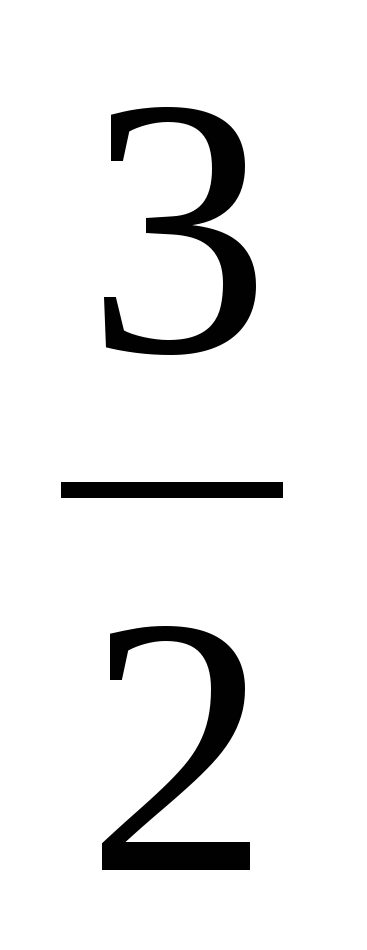A1A2.
Дано: α||β, 
ВАС, α ∩АВ= A1, β ∩АВ= A2,
α ∩АС= В1, β ∩АС= В2, A1B1 = 18 см,
AA1 = 24см, A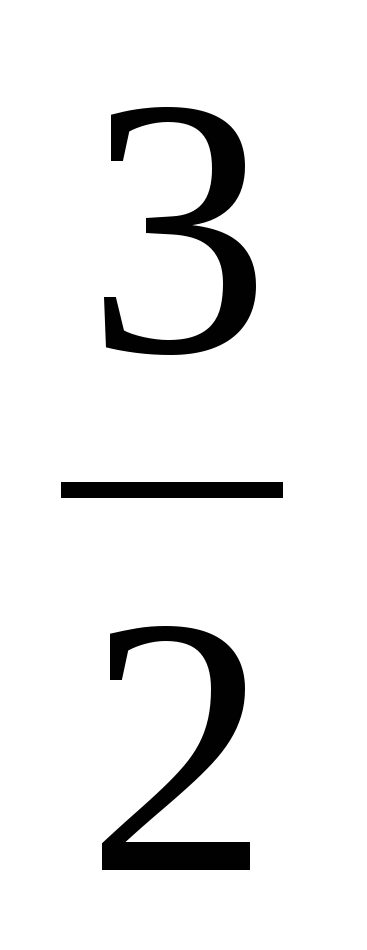A2 = A1A2.
Найти: A2B2 , AA2.
Решение: 1. α||β, (АВС) ∩ α= A1B1,
(АВС) ∩ β = A2B2 = A1B1|| A2B2
(по свойству параллельных
плоскостей)
2. ∆A2АB2: A1B1|| A2B2=∆АA1B1 ∆АA2B2= АA1/ АA2= A1В1/ A2В2
3. АA2= A1A2+24, AA2 = 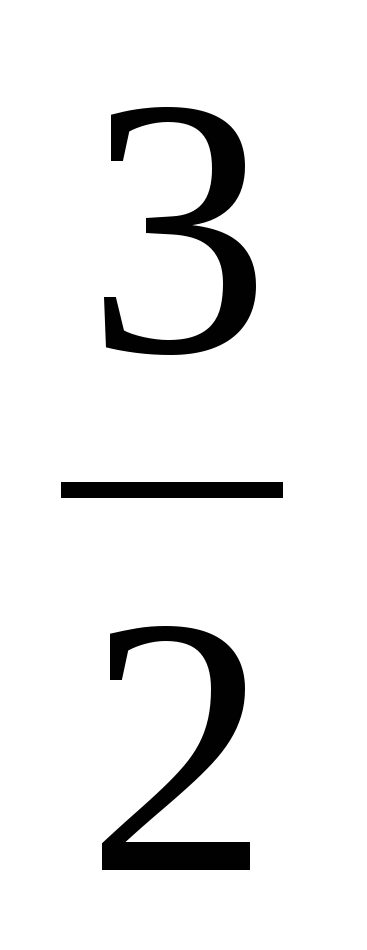A1A2 A1A2+24= 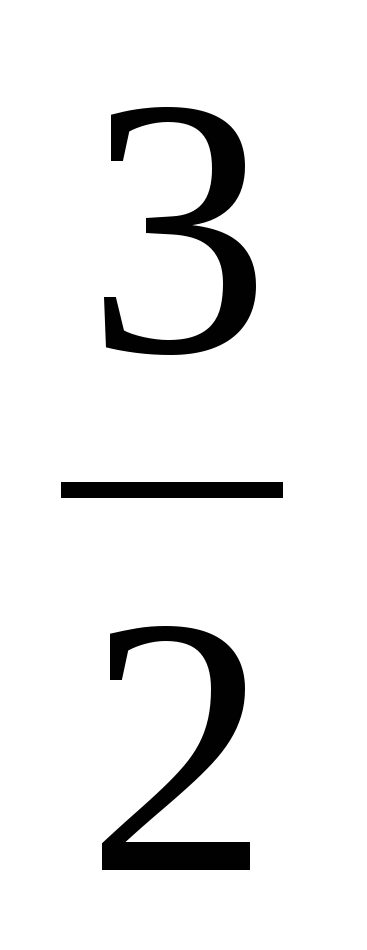A1A2,
0,5 A1A2=24,
A1A2=48(см), АA2=24+48=72(см).
Из п.2 и п.3 следует, что 24/72=18/ A2В2,
A2В2=54(см).
Ответ: АA2=72см , A2В2=54см.
№
65(а) - устно
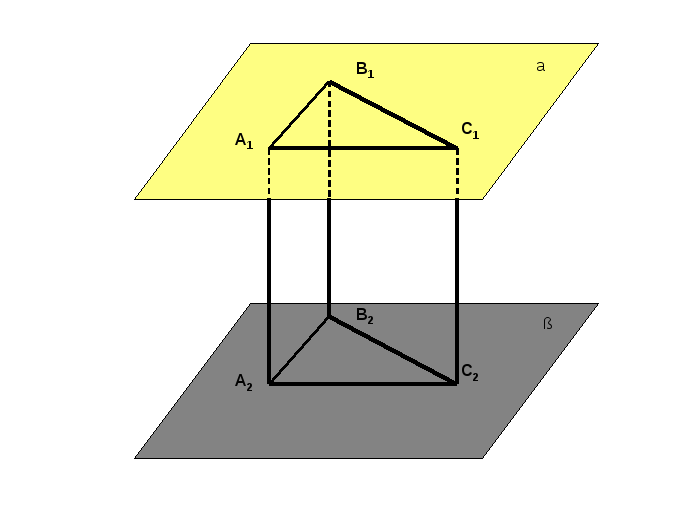
Параллельные отрезки A1A2 , В1В2 и С1С2 заключены между параллельными плоскостями α и β. Определите вид четырехугольников A1A2В1В2, A1A2В1В2 и A1A2В1В2
(Слайд 7) .
Решение: A1A2|| В1В2, A1A2= В1В2 (как отрезки параллельных прямых,
заключенные между параллельными плоскостями) = A1A2В1В2 –
параллелограмм по второму признаку. Аналогично определяется вид
четырехугольников A1A2В1В2 и A1A2В1В2 .
IV. Итоги урока .
Сформулировать свойства параллельных плоскостей.
Домашнее задание.
п.11, повт. п.10, №59, 63(а), 64.
Дополнительная задача.
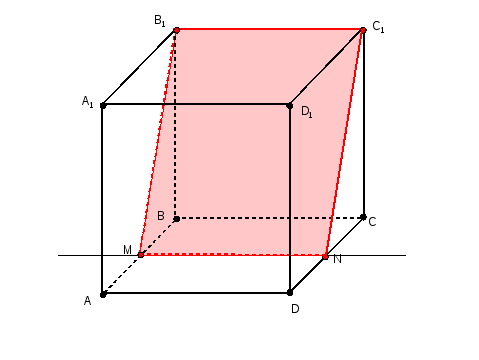
Построить сечение куба АВСDА1В1С1D1 плоскостью, проходящей через ребро В1С1 и точку, принадлежащую ребру DC.
Обсудить план решения (Слайд 8)
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
