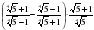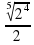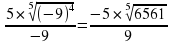Просмотр содержимого документа
«Документ Microsoft Office Word (2)»
Урок в 10 классе по алгебре и началам анализа.
Тема: Свойства корней степени n.
Цели урока:
образовательные: обобщить знания свойств корня степени n в ходе выполнения упражнений; закрепить умение преобразовывать выражения, содержащие корни степени n;
развивающие: способствовать развитию логического мышления, математической речи учащихся, внимания, памяти;
воспитательные: воспитание интереса к математике как учебному предмету через современные технологии преподавания; способствовать развитию навыков самоконтроля;
формировать компетентность информационных технологий (слайды 1-2)
Оборудование: ПК, компьютерная презентация, тест (MS Excel), ресурсы Интернета.
Ход урока
Орг. момент.
Сообщение темы и целей урока. Учащиеся на протяжении всего урока заполняют листы самоконтроля.
| Этапы урока | усвоил полностью, могу применить | усвоил полностью, но затрудняюсь | усвоил частично | не усвоил, нужна консультация |
| Проверка домашнего задания |
|
|
|
|
| Устная работа |
|
|
|
|
| Выполнение упражнений |
|
|
|
|
| Самостоятельная работа |
|
|
|
|
2 человека выполняют индивидуальные задания на доске:
1* 1) Вычислите:
а) 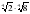 ; б)
; б) 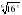 .
.
2) Вынесите множитель из-под знака корня:
а) 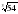 ; б)
; б) 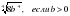 ; в)
; в) 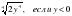 ; г)
; г) 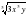 .
.
2* 1) Вычислите:  .
.
2) Избавьтесь от иррациональности в знаменателе:
а) 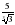 ; б)
; б) 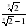 .
.
3. Остальные учащиеся выполняют задание в тетрадях :
1) Найдите значение выражения: а) 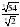 ; б)
; б) 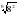 .
.
2) Вынесите множитель из-под знака корня:
а) 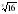 ; б)
; б)  ; в)
; в) 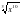
3) избавьтесь от иррациональности в знаменателе:
a)  b)
b)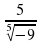
Самопроверка с записью в лист самоконтроля
№ 3.63(е)
Устная работа.
Что называется корнем n степени?
Что называется арифметическим корнем степени n?
Сформулируйте свойства арифметического корня степени n.
Имеет ли смысл выражение: 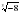 ;
; 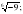

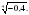
Найдите значение выражения:
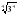 ;
;  ;
; 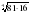 ;
; 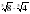 ;
; 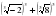 ;
; 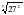 ;
;  ;
;  ;
; 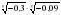
Упростите выражение:
а) 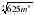 ; б)
; б) 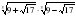
Работа с учебником : п 3.6
№ 3.67-3.377 (а,е)
Самостоятельная работа (разноуровневая) .
I уровень: учащиеся выполняют задание теста по вариантам.
I вариант.
1. Вычислите: 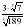 .
.
1) 1; 2) 4,5; 3) 8; 4) 21.
2. Вычислите:  .
.
1)  ; 2) −0,2; 3) −0,4; 4)
; 2) −0,2; 3) −0,4; 4) 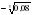 .
.
3. Упростите выражение: 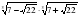 .
.
1) 3; 2) −15; 3) −3; 4) 9.
4. Упростите выражение: 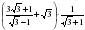 .
.
1) 2; 2)  ; 3)
; 3)  ; 4)
; 4) 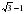 .
.
III уровень: учащиеся выполняют задания, требующие подробного описания решения
1) Упростите выражение:  .
.
2) Вычислите: 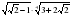 .
.
3) Упростите выражение: 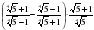
После выполнения самостоятельной работы проводится самопроверка
Задание на дом: № 3.72 (ж – и), №3.77, № 3.80, № 16 (а, в)( стр. 364)
Заполнение листа самоконтроля.
Просмотр содержимого презентации
«Презентация на тему%3A -Свойства корней степени n- »

Свойства корней степени n
Учитель: Ивашко Марина Фирсовна
МБОУ «Лицей №8»
г. Сосновый Бор
Ленинградская обл.

Проверь себя:
1.
а)
б)
2.
б)
а)
в)
3.
а)
б)

Теорема 1. Для натуральных чисел m, n (m ≥ 2, n ≥2 ) неотрицательного числа а справедливы равенства

Теорема 1.
Доказательство.
Возведём отдельно левую и правую части равенства в степень n получим равные числа:

Теорема 1.
Доказательство.
Возведём отдельно левую и правую части равенства в степень mn получим равные числа:

Теорема 1.
Доказательство.
Возведём отдельно левую и правую части равенства в степень mn получим равные числа:

Теорема 1. Для натуральных чисел m, n (m ≥ 2,n ≥2 ) неотрицательного числа а справедливы равенства
Замечание. Если m, n – нечётные, то теорема 1 справедлива для всех а Є R.

Пример 1.

Теорема 2. Для натурального числа m и действительного числа а справедливо равенство
Доказательство.
Пусть a Є R – произвольное число. Тогда
Поэтому в силу равенства
получим:
Пример 2.

Замечание. Для натурального числа m и действительного числа а справедливо равенство

Теорема 3. Пусть а – положительное число, р – целое число,
n – натуральное число ( n ≥2 ) . Тогда справедливо равенство

Теорема 3.
Доказательство.
Если р Є N , то равенство уже доказано.
Если р=0, то
Если р n из положительного числа получим:

Пример 3.

Литература
- Учебник для 10 класса общеобразовательных учреждений.
С. М. Никольский, М. К. Потапов,
Н.Н. Решетников, А. В. Шевкин.





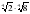 ; б)
; б) 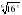 .
.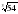 ; б)
; б) 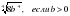 ; в)
; в) 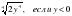 ; г)
; г) 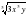 .
. .
.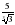 ; б)
; б) 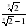 .
.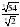 ; б)
; б) 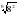 .
.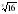 ; б)
; б)  ; в)
; в) 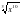

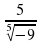
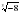 ;
; 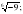

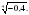
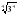 ;
;  ;
; 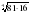 ;
; 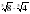 ;
; 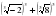 ;
; 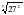 ;
;  ;
;  ;
; 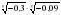
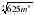 ; б)
; б) 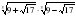

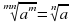

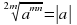

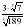 .
. .
. ; 2) −0,2; 3) −0,4; 4)
; 2) −0,2; 3) −0,4; 4) 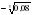 .
.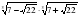 .
.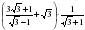 .
. ; 3)
; 3)  ; 4)
; 4) 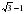 .
. .
.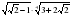 .
.