Свойства углов, образованных при пересечении двух параллельных прямых секущей

«Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».

(Галилео Галилей).

«В геометрии нет царских путей»

Евклид

Свойство углов,

образованных при пересечении

параллельных прямых

секущей.

Цели урока :

• Повторение пройденного материала.
• Закрепить умения использовать знания признаков и свойств углов, образованных при пересечении параллельных прямых секущей.
• Доказать следствие теоремы о свойствах углов, образованных при пересечении двух прямых секущей.
• Развивать логическое мышление учащихся,

самостоятельность, творческие способности.

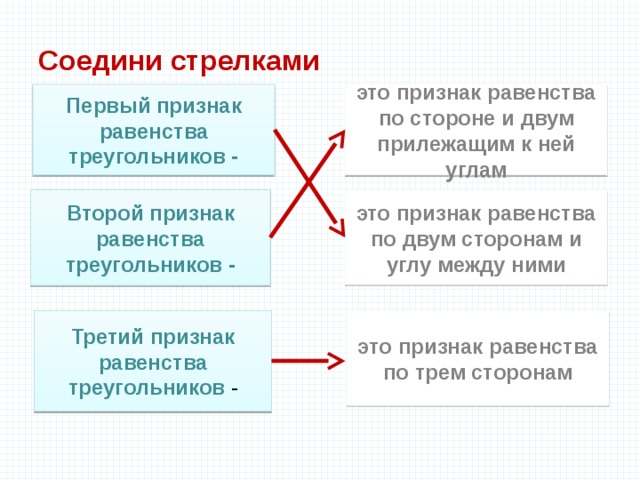
Соедини стрелками

Первый признак равенства треугольников -

это признак равенства по стороне и двум прилежащим к ней углам

Второй признак равенства треугольников -

это признак равенства по двум сторонам и углу между ними

Третий признак равенства треугольников -

это признак равенства по трем сторонам

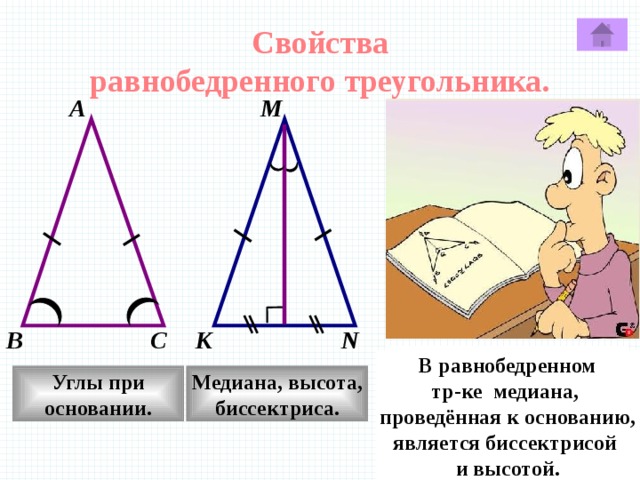
Свойства

равнобедренного треугольника.

А

М

В

К

N

С

В равнобедренном

треугольнике углы

при основании равны.

В равнобедренном

тр-ке медиана,

проведённая к основанию,

является биссектрисой

и высотой.

Медиана, высота,

Углы при

биссектриса.

основании.

Прямые

Параллельные

Пересекающиеся

Аксиома

параллельных прямых

Параллельные прямые.

Определение.

а

b

Две прямые на плоскости называются

ПАРАЛЛЕЛЬНЫМИ , если они не пересекаются.

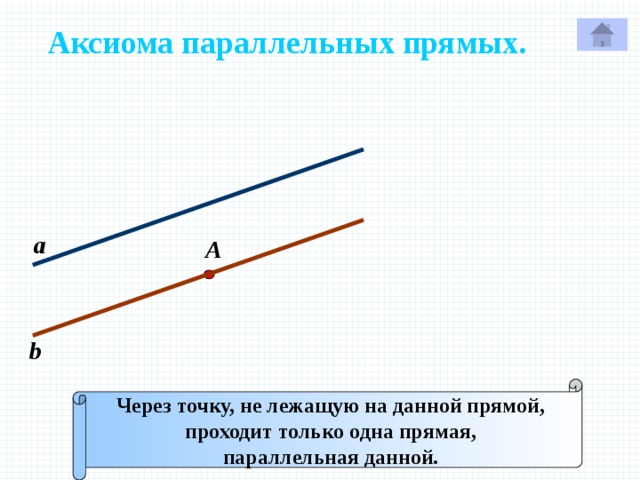
Аксиома параллельных прямых.

а

А

b

Через точку, не лежащую на данной прямой,

проходит только одна прямая,

параллельная данной.

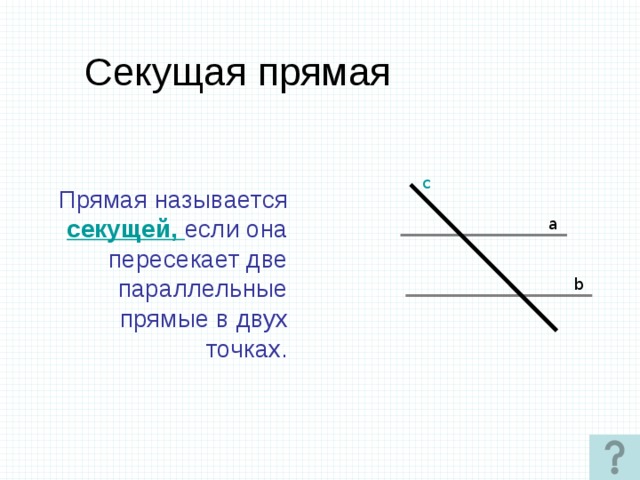
Секущая прямая

c

Прямая называется секущей, если она пересекает две параллельные прямые в двух точках.

a

b

Признаки параллельности прямых

Если при пересечении двух прямых секущей

Внутренние

Соответственные

Внутренние

накрест лежащие

углы равны

односторонние

углы равны

в сумме

180 °

ИЛИ

ИЛИ

то эти прямые параллельны .

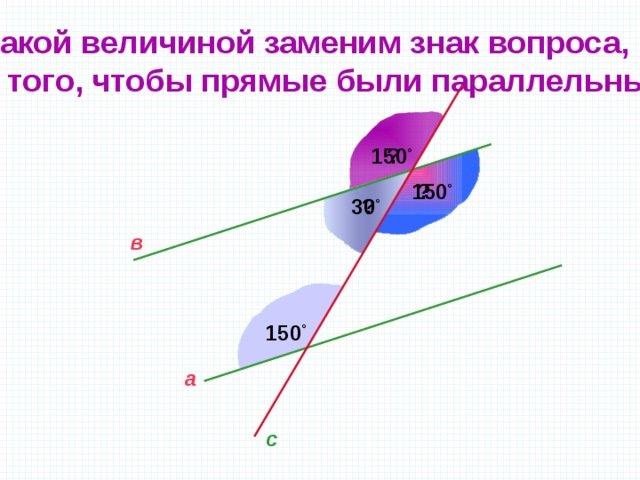
Какой величиной заменим знак вопроса,

для того, чтобы прямые были параллельны?

150 °

?

?

150 °

?

30 °

в

150 °

а

с

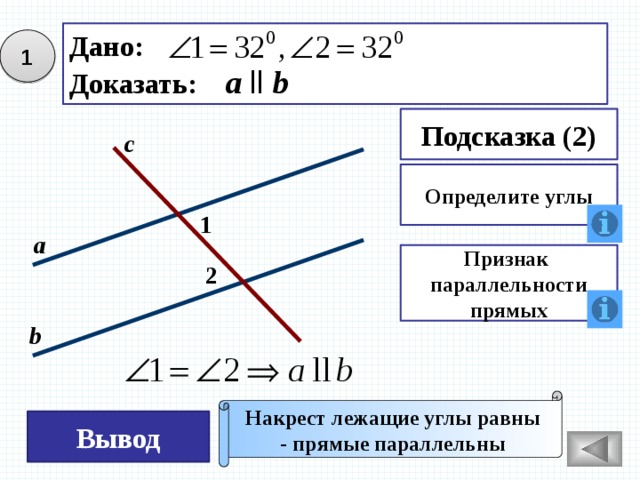
Дано:

Доказать: а ll b

1

Подсказка (2)

с

Определите углы

1

а

Признак

параллельности

прямых

2

b

Накрест лежащие углы равны

- прямые параллельны

Вывод

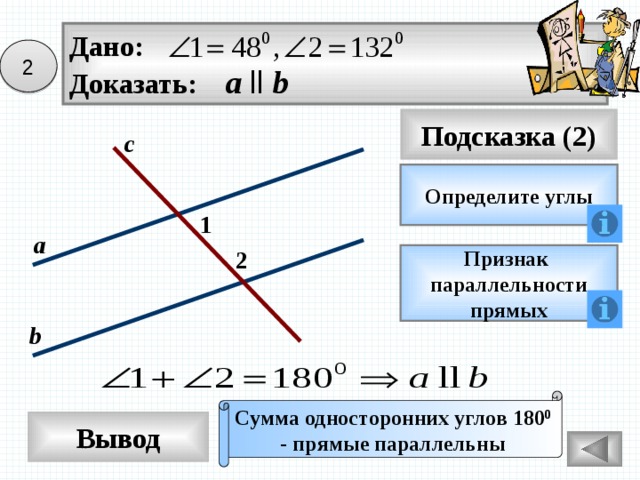
Дано:

Доказать: а ll b

2

Подсказка (2)

с

Определите углы

1

а

2

Признак

параллельности

прямых

b

Сумма односторонних углов 180 0

- прямые параллельны

Вывод

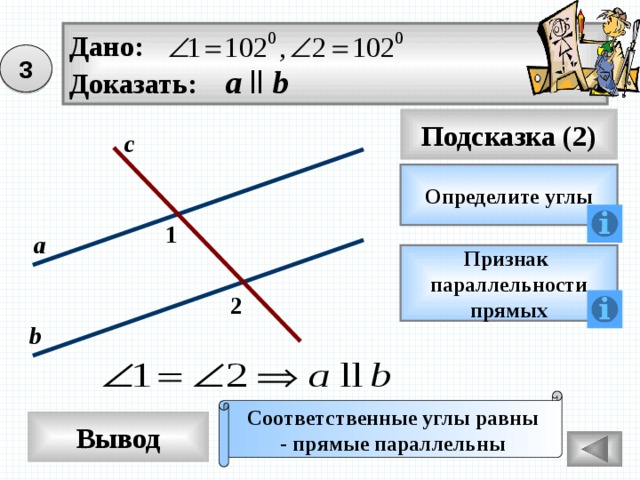
Дано:

Доказать: а ll b

3

Подсказка (2)

с

Определите углы

1

а

Признак

параллельности

прямых

2

b

Соответственные углы равны

- прямые параллельны

Вывод

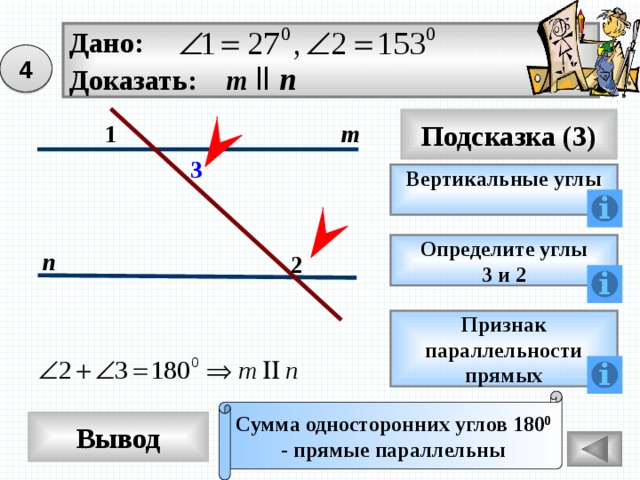
Дано:

Доказать: m ll n

4

Подсказка (3)

1

m

3

Вертикальные углы

Определите углы

3 и 2

n

2

Признак

параллельности

прямых

Сумма односторонних углов 180 0

- прямые параллельны

Вывод

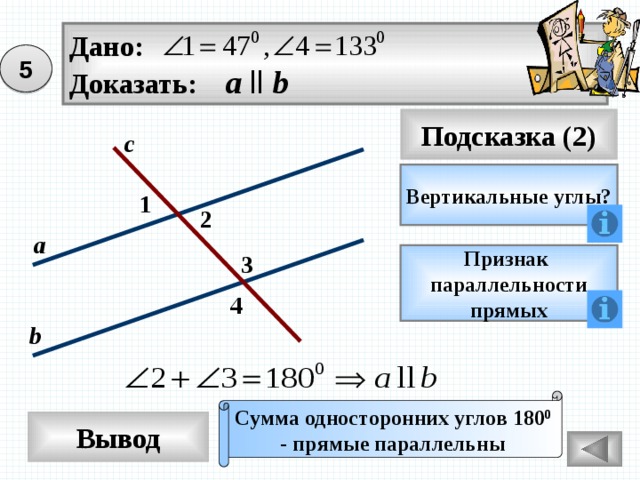
Дано:

Доказать: а ll b

5

Подсказка (2)

с

Вертикальные углы?

1

2

а

3

Признак

параллельности

прямых

4

b

Сумма односторонних углов 180 0

- прямые параллельны

Вывод

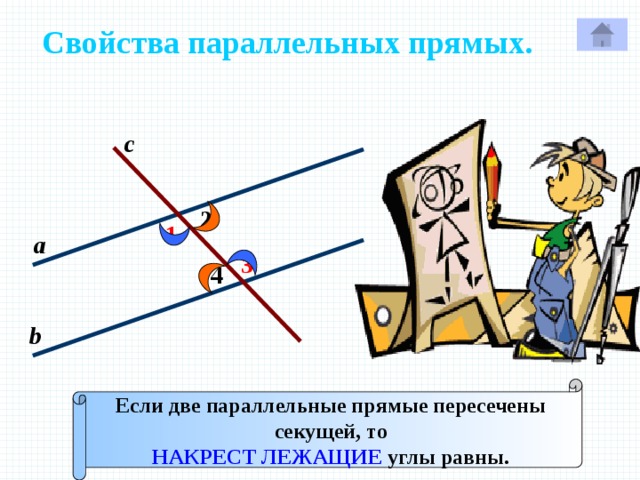
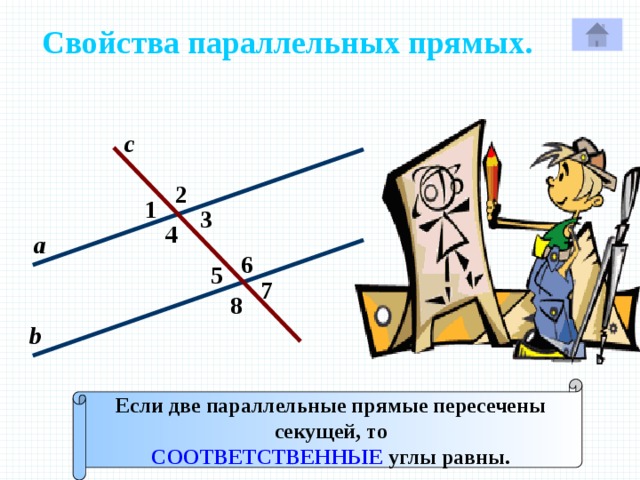
Свойства параллельных прямых.

с

2

1

а

3

4

Р

b

Если две параллельные прямые пересечены

секущей, то

НАКРЕСТ ЛЕЖАЩИЕ углы равны.

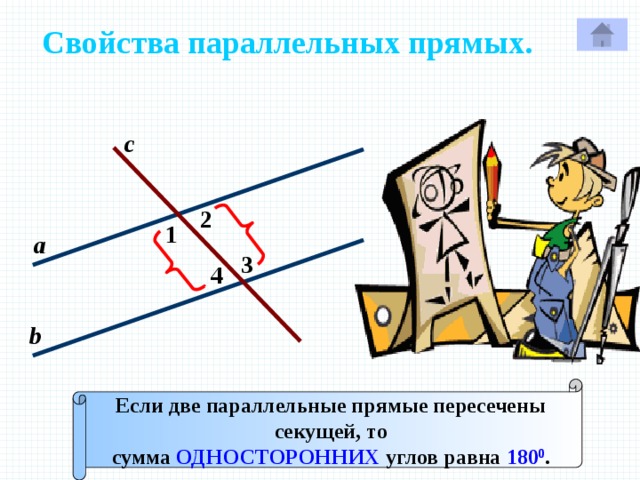
Свойства параллельных прямых.

с

2

1

3

4

а

6

5

7

Р

8

b

Если две параллельные прямые пересечены

секущей, то

СООТВЕТСТВЕННЫЕ углы равны.

Свойства параллельных прямых.

с

2

1

а

3

4

Р

b

Если две параллельные прямые пересечены

секущей, то

сумма ОДНОСТОРОННИХ углов равна 180 0 .

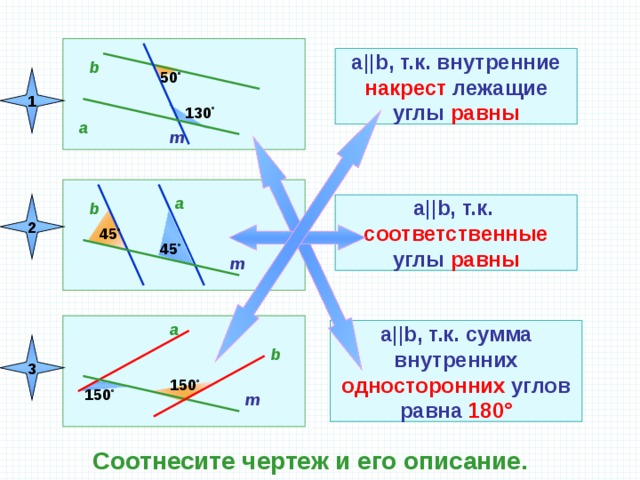
a ||b, т.к. внутренние

накрест лежащие

углы равны

b

50 °

1

130 °

a

m

a

2

a ||b, т.к.

b

соответственные

углы равны

45 °

45 °

m

a

a ||b, т.к. сумма

внутренних

односторонних углов

равна 180°

3

b

150 °

150 °

m

Соотнесите чертеж и его описание.

Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.

c

а

1

2

b

Доказательство:

Две прямые называются перпендикулярными, если они пересекаются под прямым углом (т.е.образуют четыре прямых угла.)

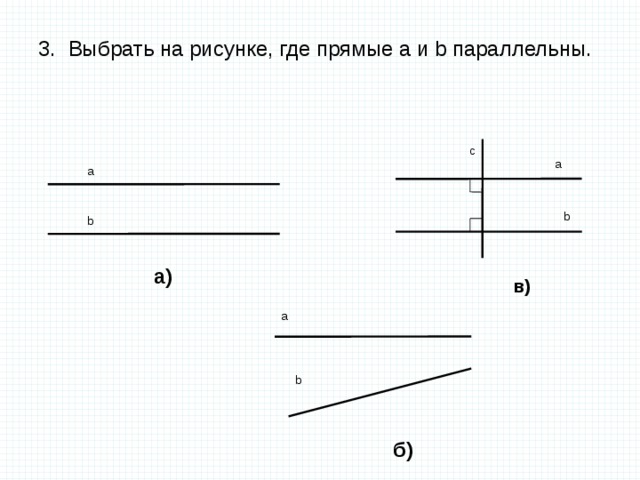
3. Выбрать на рисунке, где прямые a и b параллельны.

с

а

a

b

b

а)

в)

a

b

б)

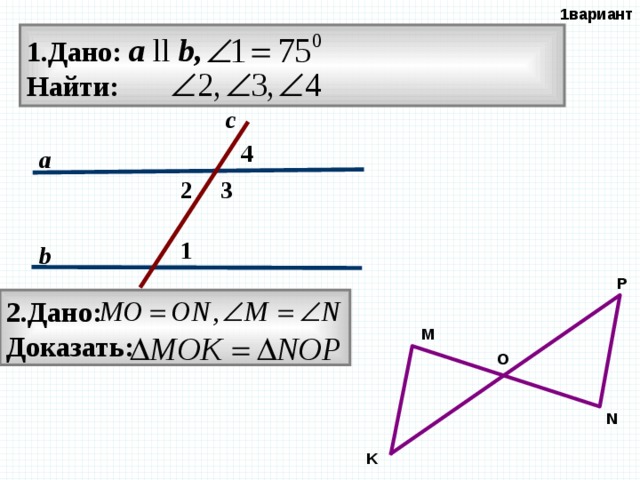
1вариант

1.Дано: а ll b,

Найти:

с

4

а

2

3

1

b

P

2.Дано:

Доказать:

M

O

N

K

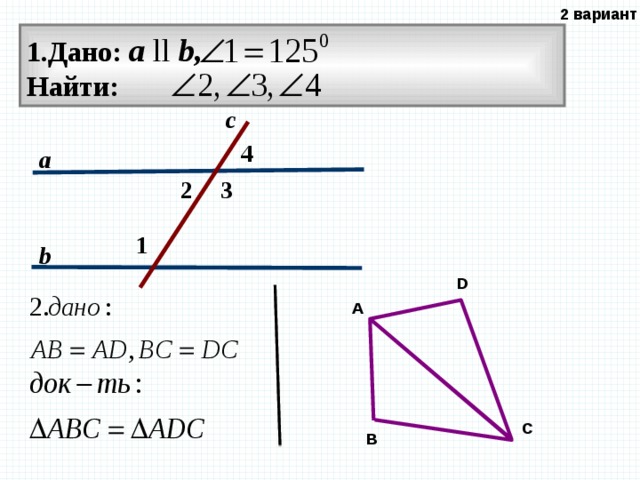
2 вариант

1.Дано: а ll b,

Найти:

с

4

а

3

2

1

b

D

A

C

B

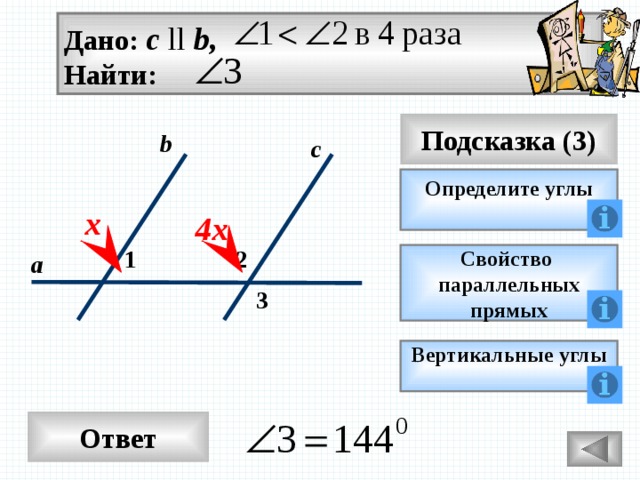
Дано: c ll b,

Найти:

Подсказка (3)

b

с

Определите углы

х

4х

2

1

Свойство

а

параллельных

прямых

3

Вертикальные углы

Ответ

Дано: а ll b,

Найти:

с

Подсказка (3)

а

3

1

Определите углы

b

Свойство

параллельных

прямых

2

Смежные углы

Ответ

Дано: а ll b,

Найти:

с

2

3

а

1

4

5

6

b

7

8

Ответ

Молодцы!

Спасибо!