Содержание
Введение…………………………………………………………………………………….........2
ГЛАВА I. ВЫЧИСЛЕНИЯ ДРЕВНОСТИ
-
История возникновения вычислений…………………………………………..……....3
-
Старинные способы быстрого счета…………………………………………….......…4
ГЛАВА II. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ БЫСТРОГО СЧЕТА
2.1. Приемы быстрого счета……………………………………………………..........................6
2.2. Практическая реализация приемов быстрого счета…………………………………..…..7
Заключение………………………………………………………………………………..……...9
Список литературы………………………………………………………………………..……10
Интернет-ресурсы…………………………………………………………………………..…..11
Приложение 1…………………………………………………………………………….……..12
Приложение 2……………………………………………………………………………...…....13
Приложение 3……………………………………………………………………………...……15
Введение
Во все времена математика была и остается одним из основных предметов в школе, потому что математические знания необходимы всем людям. Кроме того, всем школьникам предстоит сдача экзаменов в 9-м классе и в 11-м классе, а для этого, обучаясь с 1-го класса, необходимо качественно осваивать математику и прежде всего, нужно научиться считать.1
Актуальность исследования состоит в том, что в настоящее время большинство учащихся не могут обойтись без калькулятора, и соответственно не могут вычислять самостоятельно. Поэтому в данной работе хочу показать, как можно вычислять быстро и правильно и что процесс выполнения действий может быть не только полезным, но и интересным занятием.
Цель исследования: изучить приемы быстрого счета и показать необходимость их применения для упрощения вычислений.
В соответствии с поставленной целью были определены следующие задачи исследования:
-
проанализировать литературные источники по данной теме;
-
изучить приемы быстрого счета, которые можно использовать, упрощая вычисления;
-
провести диагностику и изучить результаты исследования;
-
составить памятку для учащихся 6-х классов для применения приемов быстрого счета.
Объект исследования: приемы быстрого счета.
Предмет исследования: процесс вычислений.
Гипотеза исследования: если показать, что применение приемов быстрого счета облегчает вычисления, то можно добиться того, что повысится вычислительная культура учащихся, и они найдут общий язык со сложной наукой «Математика».
Приемы и методы: опрос (анкетирование), анализ, работа с источниками информации, практическая работа, наблюдения.
ГЛАВА I. ВЫЧИСЛЕНИЯ ДРЕВНОСТИ
-
История возникновения вычислений
Мы все учились понемногу чему-нибудь и как-нибудь, писал А. С. Пушкин. Именно так и зарождалась арифметика. Жизнь заставляла наших предков осваивать основы счета, выполняя простейшие вычисления и измерения, необходимые для выживания.
Ученые полагают, что человек научился считать более 100 тыс. лет назад. Операции с вычислениями применялись во время обмена продуктами питания и орудиями труда с другими племенами, для составления календарей миграции животных, на которых охотились древние люди, и для определения времени посадки растений.
Реальными «счетными устройствами» были пальцы рук и ног, которых древним людям вполне хватало для простых расчетов. Результаты вычислений фиксировались с помощью узелков на веревках или зарубок на ветках деревьев и костях животных.
Со временем стали появляться более сложные приборы для вычислений. Первым из них считается абак, придуманный в Вавилоне в III тыс. до н. э. Абак представлял собой дощечку с углублениями, по которым передвигали косточки или ракушки, имевшие определенное числовое значение. Такие счеты служили главным образом для выполнения действий сложения и вычитания. В V в. до н. э. египтяне усовершенствовали конструкцию, начав использовать вместо линий и углублений проволоку с нанизанными камешками.2
Абак завоевал популярность во всем мире, а в ходе продолжительной эволюции сформировались три основных вида абака — китайские, японские и русские счеты. Все они сохранили свое назначение и с успехом применяются до сих пор, к примеру, на занятиях по программе «Ментальная арифметика».
Сегодня научно доказано, что счеты способствуют пониманию азов математики и совершенствованию навыков устного счета.
-
Старинные способы быстрого счета
В старину люди научились при помощи пальцев рук не только считать большие числа, но и выполнять действия сложения и вычитания. Но действия умножения и деления давалось очень трудно. «Умноженье – мое мученье, а с деленьем – беда» – говорили в старину. Тогда не существовало еще, как теперь, одного выработанного практикой приёма для каждого действия.
Рассмотрим некоторые старинные способы вычислений.
Умножение на 9 на пальцах рук.
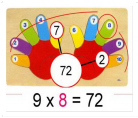 С помощью данного способа, мы можем умножить любое однозначное число на 9. Например, умножаем 9 на 8 и загибаем третий палец правой руки. Считаем количество пальцев до загнутого (слева и справа). Слева — это первый знак числа, справа — второй. В нашем случае цифры 7 и 2 дают число 72.
С помощью данного способа, мы можем умножить любое однозначное число на 9. Например, умножаем 9 на 8 и загибаем третий палец правой руки. Считаем количество пальцев до загнутого (слева и справа). Слева — это первый знак числа, справа — второй. В нашем случае цифры 7 и 2 дают число 72.
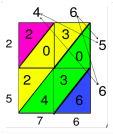 Метод решетки (аль-Хорезми).
Метод решетки (аль-Хорезми).
Н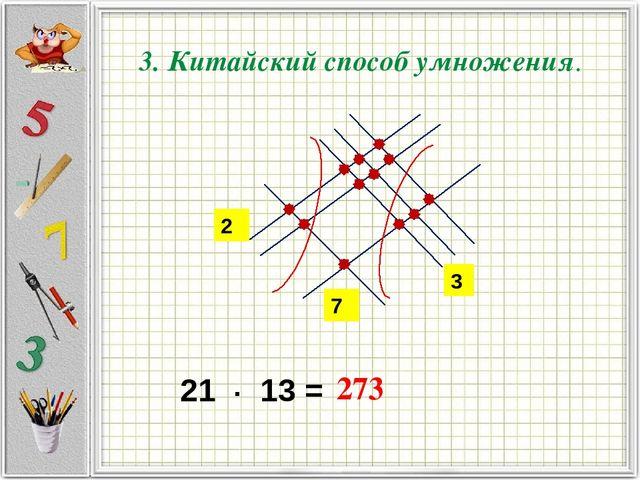 апример, нужно умножить 46 и 56. Начертим таблицу, в которой две клетки по длине и две по ширине запишем одно число по длине другое по ширине. В клетках запишем результат умножения данных цифр, на их пересечении отделим десятки и единицы диагональю. Полученные цифры сложим по диагонали, и полученный результат можно прочитать по стрелке (вниз и вправо): 46*56=2576.
апример, нужно умножить 46 и 56. Начертим таблицу, в которой две клетки по длине и две по ширине запишем одно число по длине другое по ширине. В клетках запишем результат умножения данных цифр, на их пересечении отделим десятки и единицы диагональю. Полученные цифры сложим по диагонали, и полученный результат можно прочитать по стрелке (вниз и вправо): 46*56=2576.
Японский способ умножения.
Это удивительно, но японские дети умеют умножать большие числа, даже не зная о таблице умножения. Как умножают японцы? Они делают это очень просто, настолько просто, что используют лишь базовые навыки рисования и счета. Допустим, необходимо умножить 21 на 13. Для начала нужно нарисовать одну, две и одну параллельные линии, которые будут размещаться по диагонали с верхнего левого угла в нижний правый. На созданных группах параллелей нарисовать одну и три линию соответственно. Они также будут размещаться по диагонали с нижнего левого угла в правый верхний.
Следующий этап – подсчет точек пересечения. Сначала отделяем полукругом место пересечения трех линий с одной и считаем количество точек. Получившееся число записываем под ним. Дальше точно таким же образом отделяем участки, где пересекаются две линии с одной. Также считаем точки соприкосновения и записываем, потом считаем точки, которые остались в центре. Если центральное число двузначное, то первую цифру нужно добавить к числу, что получилось при подсчете точек соприкосновения в области слева от центра. Умножив, таким образом, 21 на 13, получим 273. Этим методом можно умножать как двузначные, так и трехзначные числа. Одна проблема в том, что если придется считать такие числа, как 999, 888, 777 и т.д., то нужно будет рисовать очень много черточек.
Русско-крестьянский способ умножения.
Р усские крестьяне умели умножать и без таблицы умножения. В данном способе необходимо только уметь умножать и делить на 2. Чтобы перемножить два числа, их записываем рядом, а затем левое число делим на 2, а правое умножаем на 2. Результаты записываем в столбик, пока слева не останется 1. Остаток отбрасывается. Вычеркиваем те строки, в которых слева стоят четные числа, а оставшиеся в правом складываем.3
усские крестьяне умели умножать и без таблицы умножения. В данном способе необходимо только уметь умножать и делить на 2. Чтобы перемножить два числа, их записываем рядом, а затем левое число делим на 2, а правое умножаем на 2. Результаты записываем в столбик, пока слева не останется 1. Остаток отбрасывается. Вычеркиваем те строки, в которых слева стоят четные числа, а оставшиеся в правом складываем.3
ГЛАВА II. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ БЫСТРОГО СЧЕТА
2.1. Приемы быстрого счета
Ну-ка, в сторону карандаши!
Ни костяшек. Ни ручек. Ни мела.
Устный счет! Мы творим это дело
Только силой ума и души.
Цифры сходятся где-то во тьме,
И глаза начинают светиться,
И кругом только умные лица.
Потому что считаем в уме!4
Валентин Берестов
Изучив литературу по данной теме, мы отобрали из множества приемов быстрого счета, те которые просты в понимании и доступны каждому школьнику.
Умножение двузначного числа на 11.
«Краешки сложи, в серединку положи» - эти слова помогут легко запомнить данный способ умножения на 11.
При умножении двузначного числа на 11, нужно между цифрой единиц и цифрой десятков вписать сумму этих цифр.
Например: 23·11=253, т.к. 2+3=5, поэтому между 2 и 3 ставим цифру 5.
Чтобы умножить на 11 двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения.
Пример. 94 ∙ 11 = 9 (9 + 4) 4 = 9 (13) 4 = (9 + 1) 34 = 1034.
Умножение на 22, 33,…,99.
Чтобы двузначное число умножить на 22, 33, ..., 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 44 = 4 ∙ 11; 55 = 5 ∙ 11 и т.д. Затем произведение первых чисел умножить на 11.
Например: 15*33= 15*3*11=45*11=495.
Умножение двузначного числа на 101.
По-моему, самое простое правило: припишите ваше число к самому себе. Умножение завершено. Пример: 57 * 101 = 5757.
Объяснение: (10a+b) *101 = 1010a + 101b = 1000a + 100b + 10a + b.
Аналогично производят умножение трехзначных чисел на 1001, четырехзначных - на 10001 и т.п.
Умножение на 25, числа делящегося на 4
Чтобы умножить на 25, число, делящееся на 4, нужно его разделить на 4 и получившееся число умножить на 100.
Пример, 128*25=(128:4)*100=32*100=3200.
Быстрое возведение в квадрат числа, оканчивающегося на 5
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно цифру десятков умножить на цифру, большую на единицу, и к полученному произведению приписать справа число 25.5
Пример: 35² = 3·(3+1) и приписать 25, получим 35²= 1225;
Быстрое возведение в квадрат числа, начинающегося на 5
Для возведения в квадрат, двузначного числа, начинающегося на пять, нужно прибавить к 25 вторую цифру этого числа и приписать справа квадрат второй цифры, причем если квадрат второй цифры – однозначное число, то перед ним надо приписать цифру 0.
Пример: 56² = (25+6), приписать 6² =36, 56² = 3136.
2.2. Практическая реализация приемов быстрого счета
Счет является простым и легким делом только, когда владеешь особыми вычислительными приемами и навыками. Возможно, что с первого раза у многих не получится быстро, с ходу выполнять эти или другие подсчеты. Не беда! Для успешного обучения нужна постоянная вычислительная тренировка. Она поможет приобрести полезные навыки устного счета.
Результаты своей работы оформила в памятку, которую предложила 6-м классам. Возможно, что с первого раза не у всех получится быстро, с ходу выполнять вычисления с применением этих приемов, даже если сначала не получится использовать прием, показанный в памятке, ничего страшного, просто нужна постоянная вычислительная тренировка. Она и поможет приобрести полезные навыки быстрого счета.
Перед тем, как обрабатывать информацию, собранную из информационных источников, я провела анкетирование. Моим одноклассникам было предложено ответить на вопросы анкеты «Приёмы быстрого счёта» (Приложение 1).
В анкетировании приняли участие 44 ученика.
Проводя статистическую обработку данных, были получены следующие результаты:
-
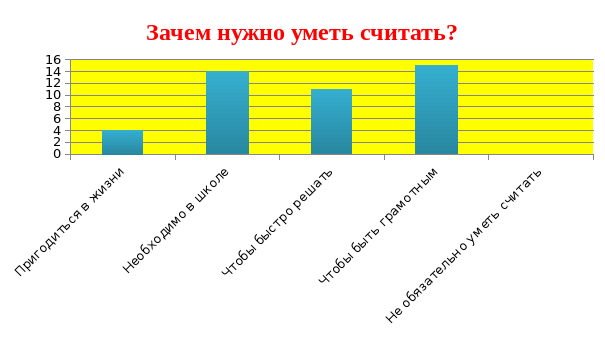
Уметь считать нужно, потому, что это пригодится в жизни, считают 4 ученика, чтобы хорошо учиться в школе – 14, чтобы быстро решать – 11, чтобы быть грамотным – 15 и не обязательно уметь считать – 0.
-
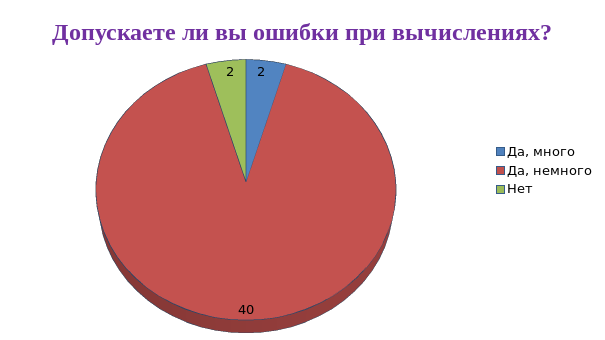
Много ошибок допускают при вычислениях 2 ученика, немного – 40 учеников и не допускают ошибок – 2 ученика.
-
Приемы быстрого счета знают 3 ученика, несколько – 13 и не знают – 28 учеников.
-
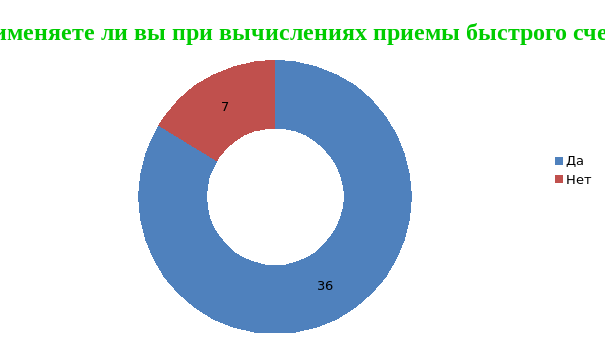
Применяют приемы быстрого счета 7 учащихся, не применяют – 37.
-
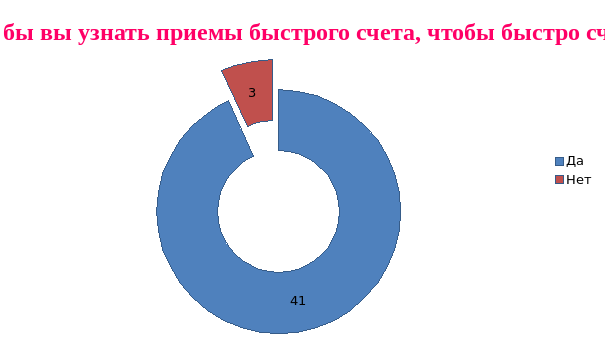
Хотели бы узнать приемы быстрого счета - 43 учащихся.
Анализ результатов показал следующее:
По результатам опроса можно сделать вывод, что большинство учеников считает, что умение считать нужно, чтобы быть грамотным и необходимо в школе, особенно для быстрого счета. Большинство опрошенных все-таки допускают вычислительные ошибки. Приемы быстрого счета знают немногие и почти все хотели бы научиться быстро считать.
Конечно, знать все способы быстрого счета невозможно, но наиболее доступные можно изучить и применять.
Заключение
Мы раскрыли тайны быстрого счета, хоть и частично. Быстрый счёт это уже не тайна за семью печатями, а научно-разработанная система. Раз есть система, значит, ее можно изучать, ей можно следовать, ею можно овладевать.6
Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попыталась показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.
В завершении нашей работы сделаем следующие выводы:
Все рассмотренные нами методы быстрого счета говорят о многолетнем интересе ученых, и простых людей к игре с цифрами.
Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении школьных предметов.
В школьных учебниках практически нет приемов быстрого счета, поэтому результат данной работы – памятка для быстрого счета будет очень полезной для учащихся 6-х классов.
Список литературы
-
Зайкин М.Н. //Математический тренинг.// - Москва, 1996.
-
Иванова Т. //Устный счёт. // Начальная школа. – 1999, №7.
-
Игнатьев Е.И. //Математическая шкатулка/ Занимательные задачи, игры, фокусы, парадоксы.// - М.:, Омега, 1994
-
Кордемский Б.А., Ахадов А.А. /Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.
-
Минских Е.М. //От игры к знаниям// М., «Просвещение», 1982г.
-
Перельман Я. И. // Математическая библиотека/ Занимательная арифметика/ Загадки и диковинки в мире чисел.
-
Перельман Я.И. / Русанова М.//Занимательная арифметика,1994 - 205с.
-
Перельман Я.И. //Быстрый счет. Тридцать простых приемов устного счета.// Л., 1941 — 12 с.
-
Свечников А.А. //Числа, фигуры, задачи// М., Просвещение, 1977г.
Интернет-ресурсы
-
http://www.mathedu.ru/lib/books/arutyunyan_levitas_zanimatelnaya_matematika_1999/#331
-
https://infourok.ru/nekotorie-priyomi-bistrogo-schyota-1242243.html
-
https://infourok.ru/issledovatelskaya-rabota-priyomi-ustnogo-bistrogo-schyota-812048.html
-
www.school.edu.ru
-
https://anisim.org/articles/priemy-bystrogo-scheta-bez-kalkulyatora/
-
https://ru.wikisource.org/wiki/Быстрый_счёт_(Перельман)
-
https://4brain.ru/blog/системы-устного-счета-и-их-создатели/
-
https://урок.рф/library/metodika_bistrogo_scheta_105526.html
-
https://papinsait.ru/shkolnye-zarisovki-v-berestov/
Приложение 1
Анкета
1. Зачем нужно уметь считать?
а) пригодится в жизни, например, считать деньги;
б) чтобы хорошо учиться в школе; в) чтобы быстро решать;
г) чтобы быть грамотным; д) не обязательно уметь считать.
2. Допускаете ли вы ошибки при вычислениях?
а) да, много; б) да, немного; в) нет.
3. Знаете ли вы приемы быстрого счета?
а) да, много; б) да, несколько; в) нет, не знаю.
4. Применяете ли вы при вычислениях приемы быстрого счета?
а) да; б) нет.
5. Хотели бы вы узнать приемы быстрого счета,
чтобы быстро считать?
а) да; б) нет.
Приложение 2
Результаты анкетирования

Приложение 3
ПАМЯТКА «НЕКОТОРЫЕ ПРИЕМЫ БЫСТРОГО СЧЕТА»
| Умножение двузначного числа на 11. При умножении двузначного числа на 11, нужно между цифрой единиц и цифрой десятков вписать сумму этих цифр. 23*11=253, т.к. 2+3=5. | Умножение на 22, 33,…,99. Чтобы двузначное число умножить на 22, 33, ..., 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 44 = 4 ∙ 11; 55 = 5 ∙ 11 и т.д. Затем произведение первых чисел умножить на 11. 15*33= 15*3*11=45*11=495. | Быстрое возведение в квадрат числа, оканчивающегося на 5. Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно цифру десятков умножить на цифру, большую на единицу, и к полученному произведению приписать справа число 25. 35² = 3·(3+1) и приписать 25, получим 35²= 1225. |
| Чтобы умножить на 11 двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения. 94 * 11 = 9 (9 + 4) 4 = 9 (13) 4 = (9 + 1) 34 = 1034. | Умножение двузначного числа на 101. Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено. 57 *101 = 5757. Аналогично производят умножение трехзначных чисел на 1001, четырехзначных - на 10001 и т.п. | Быстрое возведение в квадрат числа, начинающегося на 5. Для возведения в квадрат, двузначного числа, начинающегося на пять, нужно прибавить к 25 вторую цифру числа и приписать справа квадрат второй цифры, причем если квадрат второй цифры – однозначное число, то перед ним надо приписать цифру 0. 56² = (25+6), приписать 6² =36, 56² = 3136 |
| Умножение на 25, числа делящегося на 4. Чтобы умножить на 25, число, делящееся на 4, нужно его разделить на 4 и получившееся число умножить на 100. 128*25=(128:4)*100=32*100=3200. | 
| 
|
1� https://infourok.ru/nekotorie-priyomi-bistrogo-schyota-1242243.html
2� Иванова Т. //Устный счёт. // Начальная школа. – 1999, №7
3� http://www.mathedu.ru/lib/books/arutyunyan_levitas_zanimatelnaya_matematika_1999/#331
4� https://papinsait.ru/shkolnye-zarisovki-v-berestov/
5� Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета-12с.
6� www.school.edu.ru
11







 С помощью данного способа, мы можем умножить любое однозначное число на 9. Например, умножаем 9 на 8 и загибаем третий палец правой руки. Считаем количество пальцев до загнутого (слева и справа). Слева — это первый знак числа, справа — второй. В нашем случае цифры 7 и 2 дают число 72.
С помощью данного способа, мы можем умножить любое однозначное число на 9. Например, умножаем 9 на 8 и загибаем третий палец правой руки. Считаем количество пальцев до загнутого (слева и справа). Слева — это первый знак числа, справа — второй. В нашем случае цифры 7 и 2 дают число 72.  Метод решетки (аль-Хорезми).
Метод решетки (аль-Хорезми). апример, нужно умножить 46 и 56. Начертим таблицу, в которой две клетки по длине и две по ширине запишем одно число по длине другое по ширине. В клетках запишем результат умножения данных цифр, на их пересечении отделим десятки и единицы диагональю. Полученные цифры сложим по диагонали, и полученный результат можно прочитать по стрелке (вниз и вправо): 46*56=2576.
апример, нужно умножить 46 и 56. Начертим таблицу, в которой две клетки по длине и две по ширине запишем одно число по длине другое по ширине. В клетках запишем результат умножения данных цифр, на их пересечении отделим десятки и единицы диагональю. Полученные цифры сложим по диагонали, и полученный результат можно прочитать по стрелке (вниз и вправо): 46*56=2576.  усские крестьяне умели умножать и без таблицы умножения. В данном способе необходимо только уметь умножать и делить на 2. Чтобы перемножить два числа, их записываем рядом, а затем левое число делим на 2, а правое умножаем на 2. Результаты записываем в столбик, пока слева не останется 1. Остаток отбрасывается. Вычеркиваем те строки, в которых слева стоят четные числа, а оставшиеся в правом складываем.3
усские крестьяне умели умножать и без таблицы умножения. В данном способе необходимо только уметь умножать и делить на 2. Чтобы перемножить два числа, их записываем рядом, а затем левое число делим на 2, а правое умножаем на 2. Результаты записываем в столбик, пока слева не останется 1. Остаток отбрасывается. Вычеркиваем те строки, в которых слева стоят четные числа, а оставшиеся в правом складываем.3


























