Технологическая карта открытого урока математики по теме «Теорема Виета». 8-й класс

Деятельность учителя

Деятельность учащихся

Компетенции, УУД

0 этап. Организационный.

Цель: создать благоприятный психологический настрой.

Приветствие. Проверка готовности к уроку.

Включаются в деловой ритм урока.

Планирование сотрудничества с учителем и сверстниками.

I этап. Мотивация к учебной деятельности.

Цель: включение учащихся в учебную деятельность на личностно значимом уровне.

Ребята, прочитайте высказывание ирландского драматурга Б. Шоу: “Единственный путь, ведущий к знаниям, - это деятельность” (Аристотеля: “Познание начинается с удивления”. Клод Адриан Гельвеций: “Чтобы удивиться, достаточно одной минуты. Чтобы сделать удивительную вещь, нужны многие годы”.) Приложение 1.

Как вы понимаете это высказывание?

Дети отвечают: “Будем трудиться в поисках научной истины. Пожелаем друг другу успехов”

Смысловая саморегуляция.

Смыслообразование.

II этап. Актуализация знаний и фиксация затруднения в пробном действии.

Цель: готовность мышления учащихся и осознание потребности к построению нового способа действий.

- Какое уравнение наз. квадратным?

- Какое уравнение наз.неполным? приведённым?

- Можно ли неприведённое квадратное уравнение представить в виде приведённого? Каким образом?

Запишите на доске и в тетрадях общий вид приведённого квадратного уравнения?

Учащиеся отвечают, аргументируют.

Контроль, коррекция, оценка, волевая саморегуляция.

Умение структурировать знания, аргументация своего мнения и позиции в коммуникации.

Проверка домашнего задания:

1) Преобразуйте квадратное уравнение в приведённое и найдите его корни.(слайд)

2) Решите уравнение

(ответы называю сама, показывая, что умею решать приведённые кв. уравнения не по формуле, привлекаю гостей).

а) б) в) в ответе: 1540

г) д) : 1591

Учащиеся проверяют ответы.

Учебное сотрудничество с учителем и сверстниками.

III этап. Выявление места и причины затруднения.

Цель: Выявление и фиксация места и причины затруднения.

- А можете ли вы так же быстро решить квадратное уравнение?

- А хотите узнать?

Нет. Не знаем секрета.

Да.

Постановка и формулирование проблемы.

IV этап. Построение проекта выхода из затруднения.

Цель: постановка цели учебной деятельности, выбор способа и средств её реализации.

- Какую цель мы можем поставить на урок?

- Как бы вы сформулировали тему урока?

Научиться решать квадратные уравнения не по формуле.

Решение квадратных уравнений без формулы корней.

Целеполагание, самостоятельное выделение и формулирование познавательной цели, подведение под понятие, волевая саморегуляция, аргументация своего мнения при ответах на вопросы.

- Как вы думаете, где таится разгадка решения квадратных уравнений? (С чем могут быть связаны корни?)

- Какой у вас возникает вопрос? Что вам предстоит выяснить?

- Предположите, существует ли связь между корнями и коэффициентами? Какова она?

- Если есть версии, нужно их проверить.

Существует ли связь между корнями и коэффициентами приведённого квадратного уравнения? Если да, то какова эта связь?

Выдвижение гипотез.

V этап. Реализация построенного проекта.

Цель: построение и фиксация нового знания.

Проведём небольшую исследовательскую работу (в парах). Приложение 1.

Сделайте вывод.

Дети заполняют таблицу:

(Приложение 1).

Вывод: Все уравнения приведённые, т.к. a = 1.

Сумма корней  равна второму коэффициенту, взятому с противоположным знаком

Произведение корней  равно свободному члену.

Смыслообразование.

Оценка своего вклада в работу группы (при работе в парах), достижение договорённости и согласование общего решения.

Выбор наиболее эффективных способов решения задач.

Выражение своих мыслей, аргументация своего мнения, поиск необходимой информации из текста.

Построение логической цепи рассуждений.

Проверка выполнения заданий в группах и на доске. Вывод (записать в тетрадь):

Вывод: это утверждение верно для всех уравнений, имеющих корни. Оно называется теоремой Виета, названной в честь французского математика Франсуа Виета.

Прочитаем текст о нём, вставляя вместо пропусков коды ответов уравнений из домашнего задания 1. Приложение 2.

Мы сделали с вами важное открытие! Многие решали по формуле квадратное уравнение. Но лишь благодаря своей гениальности (и наблюдательности) Виет открыл для нас связь корней с коэффициентами и позволил устно находить корни приведённого квадратного уравнения.

Верна и обратная теорема Виета.

- Как применять теорему Виета для нахождения корней приведённого квадратного уравнения?

Познакомьтесь с решением и объясните его:

Теорема, обратная теореме Виета.

Если числа  таковы, что

то   и  - корни уравнения

Работают в парах.

Составляют алгоритм нахождения корней:

1) Определить знаки корней уравнения.

2) Подобрать пары целых чисел, произведение которых равно q.

3)  Из найденных пар чисел выбрать ту пару, которая в сумме будет

равна –p.

4) Ответ.

VI этап. Первичное закрепление с проговариванием во внешней речи.

Цель: применение нового знания в типовых заданиях.

Полученные знания нам помогут решить следующие уравнения:

Проговорите решение в парах: 1-й вариант второму рассказывает решение уравнения  . Затем 2-й вариант проговаривает первому решение уравнения 

Решили несколько типовых заданий фронтально на новый способ действий с проговариванием.

Смыслообразование.

Контроль – сличение способа действия, его результата с заданным эталоном.

Умение осознанно и произвольно строить речевое высказывание в устной и письменной форме.

Умение с полнотой выражать свои мысли в соответствии с задачами и условиями коммуникации.

VII этап. Самостоятельная работа с самопроверкой.

Цель: самопроверка умения применять новое знание в типовых условиях.

Кто разобрался в применении теоремы, обратной теореме Виета, выполняет самостоятельную работу:

(самопроверка по эталону).

Самостоятельно выполняют типовые задания на новый способ действия. Выполняют самопроверку по эталону.

Выявляют причины ошибок и исправляют их.

Контроль и коррекция, оценка.

Установление причинно-следственных связей.

Умение оформлять свои мысли.

VIII этап. Включение в систему знаний и повторение.

Цель: включение нового знания в систему знаний, повторение и закрепление ранее изученного. Если не хватает времени, то можно пропустить этот этап.

В каких заданиях вы можете использовать новую формулу?

№25.22

При решении задач.

Выполнение действий по алгоритму.

IX этап. Рефлексия учебной деятельности.

Цель: соотнесение цели урока и его результатов, самооценка работы на уроке, осознание метода построения нового знания.

Организует рефлексию и самооценку.

Заполняют рабочие листы, листы самооценки.

Оценка.

Адекватное понимание успеха/неуспеха в учебной деятельности.

X этап. Домашнее задание.

8. Домашнее задание.

1. Выучить формулировки теоремы Виета и теоремы, обратной теореме Виета.

2. Закончить доказательство теоремы Виета: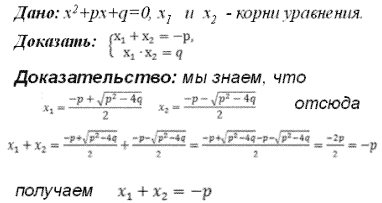

3. Учебник параграф 29, № 29.1, 29.2, 29.6, 25.32.