Техникум гидромелиорации и механизации сельского хозяйства (филиал) ФГАОУ ВО «КФУ им. В. И. Вернадского»
в пгт Советский
Технологическая карта учебного занятия
Занятие № по дисциплине Математика
Специальности 21.02.19. Землеустройство
Группы курс 1.
Тема: «Комплексные числа и действия над ними».
Цели занятия: дать определение комплексных чисел, сопряженных комплексных чисел, модуль, аргумент комплексного числа и его изображение на комплексной плоскости, ввести действия над комплексными числами, применять комплексные числа при решении квадратных уравнений с отрицательным дискриминантом.
Образовательная:
обобщить знания связанные с комплексными числами;
научиться выполнять действия над комплексными числами;
научиться вычислять модуль комплексного числа;
научиться изображать комплексные числа на плоскости;
решать квадратные уравнения с отрицательные дискриминантом;
оценить свои знания по теме.
Развивающая:
развитие зрительного анализа, внимания;
абстрактно-логического мышления;
развивать логическое мышление;
умения анализировать и делать выводы.
Воспитательная:
повышение интереса обучающихся к предмету;
развивать умение работать в группе;
воспитание прилежания, активности, внимания.
Освоение данной темы обеспечивает достижение следующих результатов:
- уметь переносить знания в познавательную и практическую области жизнедеятельности;
- уметь интегрировать знания из разных предметных областей;
- выдвигать новые идеи, предлагать оригинальные подходы и решения; и способность их использования в познавательной и социальной практике.
Тип занятия : Практическое.
Межпредметные связи: алгебра.
Технические средства обучения учебник, карточки с заданиями, ноутбук, экран.
Литература:
Булдык, Г. М. Математика / Г. М. Булдык. — 2-е изд., стер. — Санкт-Петербург : Лань, 2024. — 156 с. — ISBN 978-5-507-48578-9. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/356150.
Блинова, С. П. Математика. Практикум для студентов технических специальностей : учебное пособие для спо / С. П. Блинова. — 3-е изд., стер. — Санкт-Петербург : Лань, 2024. — 196 с. — ISBN 978-5-507-49222-0. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/383441.
Богомолов, Н. В. Алгебра и начала анализа : учебное пособие для среднего профессионального образования / Н. В. Богомолов. — Москва : Издательство Юрайт, 2024. — 240 с. — (Профессиональное образование). — ISBN 978-5-534-09525-8. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/536960.
Структура занятия:
1.Организационный момент.(5 мин.)
2. Подготовка учащихся к активному сознательному усвоению знаний (актуализация знаний учащихся) (10 мин)
3. Повторение материала (20 мин)
4.Закрепление новых знаний (ответы на вопросы, решение задач и примеров) (30 мин)
5. Самостоятельное решение практических заданий. (15 мин)
5. Информация о домашнем задании, методические указания по его выполнению. (5 мин)
6.Рефлексия. Подведение итогов.(5 мин).
Ход занятия
Краткие теоретические сведения
Комплексным числом называется выражение вида a+bi , где a и b –действительные числа, а i-мнимая единица. Множество комплексных чисел обозначается через C.
Запись комплексного числа в виде a+ bі называется алгебраической формой комплексного числа.
Геометрическая интерпретация комплексного числа
Комплексное число z = a+ bі можно изобразить точкой Z плоскости с координатами (a, b). Комплексное число z = a+ bі можно изобразить в виде вектора 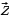 с началом в точке О (0; 0) и концом в точке Z (а; b).
с началом в точке О (0; 0) и концом в точке Z (а; b).
Изобразить на плоскости числа: z1=5; z2= -3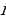 ; z3=3+2
; z3=3+2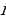 ; z4=5-2
; z4=5-2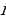 ; z5=-3+2
; z5=-3+2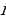 ; z6= -1-5
; z6= -1-5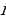 .
.
Решение.
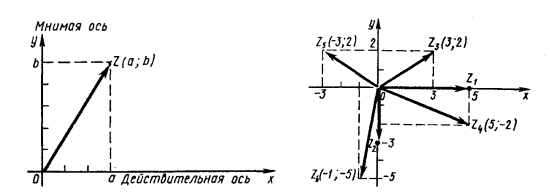
Модулем комплексного числа z = a+bі называется длина вектора 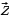 , которую можно найти по формуле
, которую можно найти по формуле 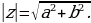
Пример. z=1-7i.
Решение. а=1, b=-7‚ то 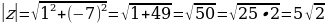
Задание 1. Изобразить на комплексной плоскости и найти модули комплексных чисел:
1. 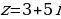 2.
2. 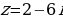 3.
3. 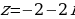
4. 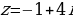 5.
5. 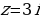 6.
6. 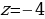
Действия над комплексными числами в алгебраической форме
Сумма: z1 = 2+3і и z2=5-7і
Решение: z1 + z2 = (2+3і) + (5-7і) = 2+3і+5-7і=(2+5)+(3і-7і)=7-4і
Разность:
Решение (2+3і)−( 5-7і)= 2+3і-5+7і=(2-5)+(3і+7і)=-3+10і
Произведение:
Решение:
z1 z2= (2+3і)(5-7і)= 10-14і+15і -21і2=10-14і+15і-21·(-1)= (10+21)+(-14і+15 і) =31+ і (замечание: здесь учтено, что i2 = – 1).
Задание 2. Вычислите:
1. (3 + 5i) + (7 – 2i). 2. (6 + 2i) + (5 + 3i)
3. (– 2 + 3i) + (7 – 2i). 4. (5 – 4i) + (6 + 2i).
5. (3 – 2i) - (5 + i). 6. (4 + 2i) - (– 3 + 2i).
7. (– 5 + 2i) - (5 + 2i). 8. (– 3 – 5i) - (7 – 2i)
9. (2 + 3i)·(5 – 7i). 10. (6 + 4i)·(5 + 2i).
11. (3 – 2i)·(7 – i). 12. (– 2 + 3i)·(3 + 5i).
13. (1 –i)·(1 + i). 14. (3 + 2i)·(1 + i).
15. (6 + 4i)·3i. 16. (2 – 3i)·(– 5i).
Комплексные числа а + bi и а – bi называются сопряженными комплексными числами. Они отличаются друг от друга только знаками перед мнимой частью.
(а + bi)(а - bi) = а2 + b2.
Для выполнения деления двух комплексных чисел необходимо произвести дополнительное действие: умножить делимое и делитель на комплексное число, сопряженное делителю.
Пример, выполнить деление: 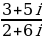
Решение
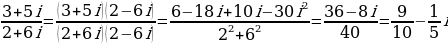
Задание 3. Выполнить деление:
1. 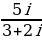 2.
2. 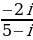 3.
3. 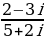
4.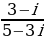 5.
5. 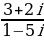 6.
6. 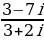
7. 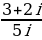 8.
8. 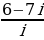 9.
9. 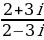
Решение квадратных уравнений с отрицательным дискриминантом:
Решим квадратное уравнение: 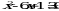 .
.
Найдем дискриминант по формуле: 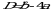 . Учитывая, что
. Учитывая, что 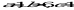 , получим:
, получим: 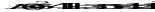 . Тогда
. Тогда 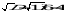 . Корни уравнения находим по формулам^
. Корни уравнения находим по формулам^ 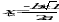 ;
;
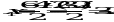 ;
; 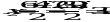 .
.
Ответ: 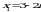 ,
, 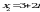 .
.
Задание 4
Решите уравнения:
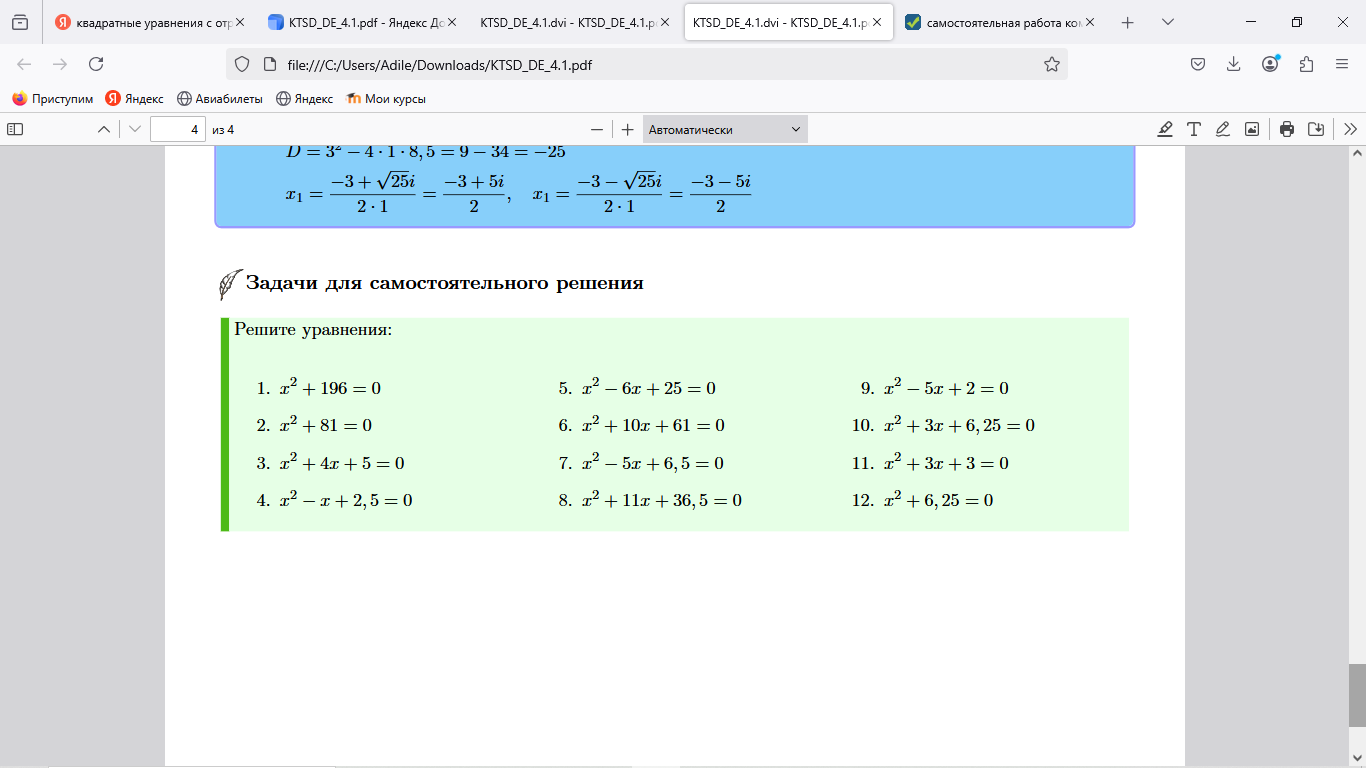
Домашнее задание
Задание 1. Изобразите на плоскости заданные комплексные числа и найдите их модули
| z1= -5i z2 = 3 + 4i |
| z3= - 2 +i z4= 6 |
Задание 2. Произведите сложение и вычитание
А) (3 + 2i) + (1 – 4i). б) (– 5 + 3i) - (8 – 2i).
Задание 3. Произведите умножение
a) (2 + 5i)(9 – 3i). б) (4 – i)(6 +7i).
Задание 4. Выполните деление комплексных чисел:
а) 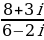
Задание 5. Решите уравнение.
а) x2 - 2x + 5 = 0.
Вопросы для проверки
Что называется комплексным числом?
Как геометрически изображаются комплексные числа?
Какие комплексные числа называются сопряженными?
Какие действия над комплексными числами можно выполнять?







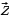 с началом в точке О (0; 0) и концом в точке Z (а; b).
с началом в точке О (0; 0) и концом в точке Z (а; b).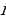 ; z3=3+2
; z3=3+2
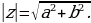
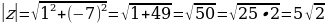
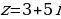 2.
2. 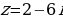 3.
3. 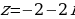
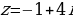 5.
5. 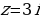 6.
6. 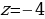
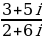
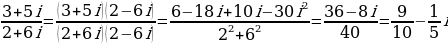
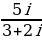 2.
2. 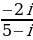 3.
3. 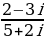
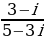 5.
5. 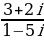 6.
6. 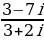
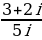 8.
8. 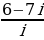 9.
9. 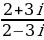
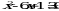 .
.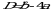 . Учитывая, что
. Учитывая, что  , получим:
, получим: 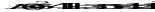 . Тогда
. Тогда 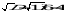 . Корни уравнения находим по формулам^
. Корни уравнения находим по формулам^ 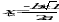 ;
; 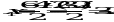 ;
; 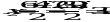 .
.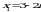 ,
, 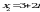 .
.