| Организационная структура урока |
| Этап урока | Содержание деятельности учителя | Содержание деятельности обучающегося
(осуществляемые действия) | Формируемые способы
деятельности |
| I. Организационный момент | Приветствует обучающихся; проверяет их готовность к уроку. Создает в классе атмосферу психологического комфорта. – О чем вы сейчас думаете? Что нам поможет сосредоточить ваше внимание на уроке геометрии? | Настраиваются на учебную деятельность. Концентрируют внимание на работе во время урока.
| Формируют навыки самоорганизации |
| II. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | Предлагает учащимся рассказать, что им уже известно о геометрических преобразованиях.
Вопрос запуска постановки учебной задачи: – Достаточно ли у вас знаний о понятии «преобразование фигуры»? Формулирует учебную задачу: – Исследовать преобразование фигуры | Принимают участие в беседе. –Я знаю… – Я могу объяснить… – Я могу выделить… Осознают важность решения поставленной учебной задачи. | Развивают навыки целеполагания |
| III. Сообщение темы. Постановка цели и задач урока | Сообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока. – Внимательно прочитайте тему урока. – Что от вас ожидается на уроке? – Какие цели и задачи вы можете перед собой поставить? | Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока: – понять, что такое преобразование фигуры; – научиться осуществлять параллельный перенос | Формируют умения принимать и сохранять учебную задачу |
| IV. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов: – Что я намерен делать сегодня на уроке геометрии? – Хочу ли я узнать о преобразовании фигур? – Что я хочу достигнуть в процессе изучения геометрии? – Как мне настроиться на работу на уроке? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Формируют умения выражать свои мысли. Развивают навыки самомотивации |
| V. Создание ситуации затруднения. Работа над темой урока | Организует обсуждение проблемного вопроса: – Каким образом может осуществляться преобразование фигуры?
Организует анализ определения понятия «преобразование фигуры». Отвечает на вопросы. Поощряет учащихся проводить дополнительные исследования.
Предлагает проанализировать свойства движения.
Создает условия для изучения определения.
Объясняет учащимся: – Если существует движение, при котором фигура 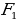 является образом фигуры F, то обязательно существует движение, при котором фигура F является образом фигуры является образом фигуры F, то обязательно существует движение, при котором фигура F является образом фигуры 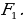 Такие движения называют взаимно обратными. Такие движения называют взаимно обратными. Организует анализ теоремы. Отвечает на вопросы учащихся. Обращает внимание на следствие теоремы: – Если фигура 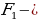 образ фигуры образ фигуры 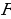 при параллельном переносе, то при параллельном переносе, то 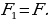 Организует совместное с учащимися решение задачи: – Точка 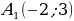 является образом точки является образом точки 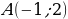 при параллельном переносе на вектор при параллельном переносе на вектор 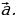 Найдите координаты вектора Найдите координаты вектора 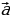 и координаты образа точки и координаты образа точки 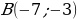 | Принимают участие в обсуждении проблемного вопроса. Предлагают гипотезы. Отстаивают свои идеи. Обсуждают идеи одноклассников. Планируют проведение исследований. Анализируют определение. Формулируют вопросы учителю. Осуществляют дополнительные исследования. | Определение | Ключевые слова | Вопросы учителю | | Преобразование фигуры F, сохраняющее расстояние между точками, называют движением (перемещением) фигуры F | Сохранение расстояния между точками | Каким образом…? | Анализируют информацию. | Информация | Понимаю (+) / Не понимаю (–) | | Если преобразование является движением, то: – образом прямой является прямая; – образом отрезка является отрезок, равный данному; – образом угла является угол, равный данному; – образом треугольника является треугольник, равный данному |
| Изучают определение. | Определение | Надо уточнить… Нужно понять… | | Две фигуры называют равными, если существует движение, при котором одна из данных фигур является образом другой |
| Делают записи в тетради. Задают вопросы.
Анализируют теорему. Задают вопросы учителю. | Теорема | В доказательстве теоремы мне непонятно… | Вопросы учителю | | Параллельный перенос является движением | Как…? | Почему…? | Совместно с учителем решают задачу. | Решение задачи | Мне непонятно… | | Из условия следует, что 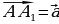 . . Отсюда 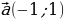 | Почему…? | | Пусть 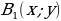 – образ точки – образ точки 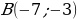 | Что…? | | Тогда 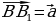 , т.е. , т.е. 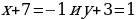
Отсюда 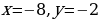 | Как…? |
| Выражают свои мысли в соответствии с задачей.
Анализируют информацию
|
| VI. Закрепление изученного материала | Предлагает учащимся почувствовать себя учителем и объяснить одноклассникам, что представляет собой преобразование фигуры. Определяет лучшие «уроки». Рекомендует некоторым учащимся задуматься о профессии учителя | Проводят фрагменты урока. Обсуждают педагогические успехи своих одноклассников |
|
| VII. Решение заданий | 1. (№ 633) Даны прямая а и отрезок АВ, не имеющий с ней общих точек. Каждой точке Х отрезка АВ поставлено в соответствие основание перпендикуляра, опущенного из точки Х на прямую а. При каком взаимном расположении прямой а и отрезка АВ описанное преобразование является движением? 2. (№ 636) Вектор 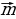 параллелен прямой а. Какая фигура является образом прямой а при параллельном переносе на вектор параллелен прямой а. Какая фигура является образом прямой а при параллельном переносе на вектор 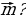 | 1. АВ а.
2. Так как 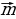 а, то образом а является сама прямая а а, то образом а является сама прямая а | Развивают умения самостоятельно принимать решения |
| VIII. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами: – Достиг ли я поставленных целей и задач урока? – Что оказалось не до конца понятным? – Чему я научился? – Доволен ли моей работой на уроке учитель? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию | Отслеживают цель учебной деятельности |
| IX. Домашнее задание | Помогает учащимся выбрать задания из учебника. Обращает внимание на возможности и способности учащихся | Выбирают задания, которые будут решать дома. Записывают домашнее задание. | Формируют навыки самоорганизации |







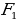 является образом фигуры F, то обязательно существует движение, при котором фигура F является образом фигуры
является образом фигуры F, то обязательно существует движение, при котором фигура F является образом фигуры 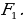 Такие движения называют взаимно обратными.
Такие движения называют взаимно обратными.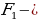 образ фигуры
образ фигуры 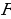 при параллельном переносе, то
при параллельном переносе, то 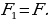
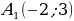 является образом точки
является образом точки 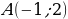 при параллельном переносе на вектор
при параллельном переносе на вектор 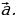 Найдите координаты вектора
Найдите координаты вектора 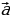 и координаты образа точки
и координаты образа точки 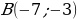

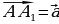 .
.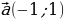
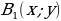 – образ точки
– образ точки 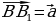 , т.е.
, т.е.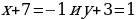
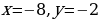
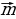 параллелен прямой а. Какая фигура является образом прямой а при параллельном переносе на вектор
параллелен прямой а. Какая фигура является образом прямой а при параллельном переносе на вектор