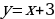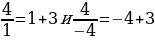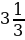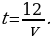| Организационная структура урока |
| Этап урока | Содержание деятельности учителя | Содержание деятельности обучающегося
(осуществляемые действия) | Формируемые способы
деятельности |
| I. Организационный момент | Приветствие. Проверка готовности обучающихся к уроку. Создание в классе атмосферы психологического комфорта. – Все ли готовы получать новые знания? – Что нам мешает настроиться на учебную деятельность? | Настраиваются на учебную деятельность. Концентрируют внимание на работе на уроке.
| Формирование навыков самоорганизации |
| II. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | Предлагает учащимся продолжить предложения: – Функцией называют…
– Все значения, которые принимает аргумент, образуют… – Все значения, которые принимает зависимая переменная, образуют… – Функцию считают заданной, если указаны…
– Способы задания функции: … – Графиком функции f называют …
– Фигура, изображенная на координатной плоскости, может быть графиком некоторой функции, если …
Вопрос запуска постановки учебной задачи: – Достаточно ли у вас знаний о функции 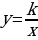 и ее графике? и ее графике? Формулирует учебную задачу: – Исследовать функцию 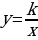 и ее график и ее график | Выполняют задание. – … правило, с помощью которого для каждого значения независимой переменной можно найти единственное значение зависимой переменной. – …область определения функции.
– …область значений функции. – …ее область определения и правило, с помощью которого можно для каждого значения независимой переменной найти значение зависимой переменной. – …формулы, табличный, графический. – …геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции f.
– …любая прямая, перпендикулярная оси абсцисс, имеет с этой фигурой не более одной общей точки. Осознают важность решения поставленной учебной задачи | Развитие навыков целеполагания |
| III. Сообщение темы. Постановка цели и задач урока | Сообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока. – Внимательно прочитайте тему урока. – Что от вас ожидается на уроке? – Какие цели и задачи вы можете перед собой поставить? | Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока: – усвоить основные понятия, связанные с функцией 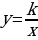 ; ; – научиться строить график функции 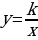 | Умение принимать и сохранять учебную задачу |
| IV. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов. – Что меня заинтересовало в теме урока? – Почему для меня важно изучить функцию 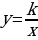 ? ? – Чего я ожидаю от сегодняшнего урока? – Где я смогу применить полученные знания и умения? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Умение выражать свои мысли. Развитие навыков самомотивации |
| V. Создание ситуации затруднения. Работа над темой урока | Организует обсуждение проблемного вопроса: – Что собой представляет график функции 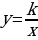 ? ? Предлагает проанализировать определение. Объясняет, что областью определения функции 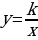 являются все числа, кроме 0. являются все числа, кроме 0.
Предлагает провести исследование и выяснить, имеет ли график функции 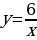 общие точки с осью ординат и осью абсцисс. общие точки с осью ординат и осью абсцисс. Помогает построить график данной функции и его проанализировать. 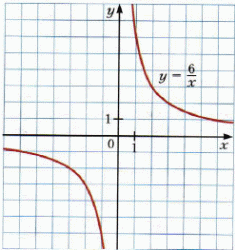
Предлагает проанализировать информацию. Отвечает на вопросы учащихся.
Совместно с учащимися выделяет основные свойства функции 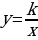 . .
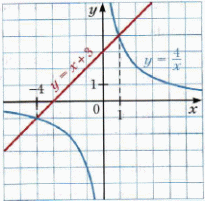
Предлагает проанализировать решение задания: – Решите уравнение 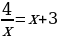
| Принимают участие в обсуждении проблемного вопроса. Испытывают определенные трудности при ответе на вопрос. Анализируют информацию.
Заполняют таблицу. | Определение | Мне непонятно… | Вопросы учителю | | Функцию, которую можно задать формулой вида 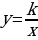 , где , где 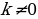 , называют обратной пропорциональностью , называют обратной пропорциональностью |
| Как…?
Что…? | Проводят исследование. Выясняют, что: – функция 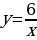 не имеет общих точек с осью ординат и с осью абсцисс; не имеет общих точек с осью ординат и с осью абсцисс; – чем больше модуль аргумента, тем меньше модуль соответствующего значения функции; – с уменьшением модуля абсциссы расстояния от точек графика до оси ординат уменьшаются и могут стать сколь угодно малыми, но никогда не будут равны нулю.
Анализируют информацию. | Информация | Вопросы учителю | | Фигуру, являющуюся графиком функции 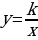 , где , где 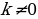 , называют гиперболой , называют гиперболой | Почему…? | | Гипербола состоит из двух частей – ветвей гиперболы | Каким образом…? | Совместно с учителем заполняют таблицу, где указывают свойства функции 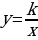 : : | Область определения | Все числа, кроме 0 | | Область значений | Все числа, кроме 0 | | График | Гипербола | | Нуль функции | Не существует | | Свойство графика | Начало координат является центром симметрии гиперболы | Анализируют решение уравнения. Выявляют логику решения. Задают вопросы учителю. | Решение задания | Мне непонятно… Вопросы учителю… | | Построим в одной системе координат графики функций 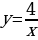 и и 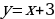 |
| | Они пересекаются в двух точках, абсциссы которых равны 1 и –4 |
| | В каждой из точек пересечения графиков значение функции 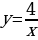 равно значению функции равно значению функции 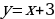 |
| | Числа 1 и –4 являются корнями уравнения 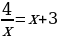 |
| | Проверка: 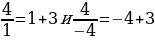 |
|
| Умение выражать свои мысли в соответствии с учебной задачей. Анализ информации.
|
| VI. Закрепление изученного материала | Организует конкурс на лучший вопрос по изученному на уроке материалу
| Придумывают вопросы. Отвечают на вопросы одноклассников. Определяют лучший вопрос. Например: – Как можно построить гиперболу? Почему 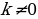 ? ? – Какие свойства графика 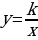 ? ? | Умение осуществлять актуализацию знаний и умений |
| VII. Решение заданий | Практические задания: 1. (№ 315) Пешеход прошел 12 км. Заполните таблицу, в первой строке которой указана скорость, а во второй – время движения. | v, км/ч | 5 |
| 2,4 |
| | t, ч |
| 3 |
| 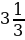
| Задайте формулой зависимость t от v. 2. (№ 317) Бригада из семи рабочих с одинаковой производительностью труда может выполнить некоторое производственное задание за 12 дней. Сколько потребуется рабочих с такой же производительностью труда, чтобы выполнить это задание за 4 дня? | Решения: 1. 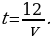
| v, км/ч | 5 | 12 : 3 = 4 | 2,4 | 12 : 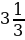 = 3,6 = 3,6 | | t, ч | 12 : 5 = 2,4 | 3 | 12 : 2,4 = 5 | 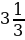
|
2. 1) 12 : 4 = 3(р.) – ускорится работа. 2) 7 . 3 = 21 (раб.) – потребуется для выполнения задания за 4 дня Ответ: 21 рабочий. | Умение самостоятельно принимать решения |
| VIII. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами. – Могу ли я объяснить, какую функцию называют обратной пропорциональностью? – Какая информация на уроке для меня была новой? – Чему я научился на уроке? – Доволен ли я результатами своей работы на уроке? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию. | Умение отслеживать цель учебной деятельности |
| IХ. Домашнее задание | Помогает учащимся выбрать задания из учебника. Обращает внимание на возможности и способности учащихся | Выбирают задания, которые будут решать дома. Записывают домашнее задание. | Формирование навыков самоорганизации |







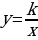 и её график» (8 класс, учебник А.Г Мерзляк, В.Б. Полонский, М.С. Якир)
и её график» (8 класс, учебник А.Г Мерзляк, В.Б. Полонский, М.С. Якир)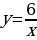 общие точки с осью ординат и осью абсцисс.
общие точки с осью ординат и осью абсцисс.

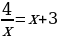
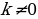 , называют обратной пропорциональностью
, называют обратной пропорциональностью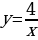 и
и