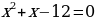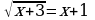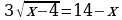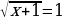Преподаватель: Белова Н.В.
Предмет: Математика
Дата: 25.02.2025
Группа: 11
Технологическая карта урока
| Тема | Иррациональные уравнения |
| Цель | Ввести понятие иррационального уравнения и показать способ решения через проверку корней способом подставки в исходное уравнение. |
| Задачи | Развивающая: Способствовать развитию навыка решения иррациональных уравнений. Воспитательная: Воспитывать навыки аккуратности и правильности оформления уравнения в тетрадях. |
| Тип урока | Урок объяснения нового материала |
| Применяемая технология | Информационно-коммуникативные технологии |
| Оборудование | Компьютер, проектор, мультимедийная презентация, учебники. |
| Основные понятия | Иррациональные уравнения |
| Формируемые универсальные учебные действия
| Предметные: знать: методы решения иррациональных уравнений; методы проверки корней уравнения. уметь: решать иррациональные уравнения. Метапредметные: познавательные – уметь ставить цели и находить пути решения; уметь анализировать текст учебника; регулятивные – осознавать качество и уровень учебного материала; коммуникативные – уметь формулировать и аргументировать собственные суждения; работать индивидуально и в группе; уметь слушать учителя и других учащихся; Личностные: уметь грамотно излагать свои мысли в устной и письменной речи; формирование ответственного отношения к учению; развитие настойчивости в достижении поставленной цели; формирование позитивной самооценки. |
| Источники информации | 1. Ш.А. Алимов Математика: алгебра и начала математического анализа, геометрия – учеб. для студ. учреждений сред. проф. образования. 2023;
|
Структура урока
| Этап | Деятельность преподавателя | Деятельность обучающихся |
| Инициализация | - приветствие - постановка учебных задач урока | приветствуют учителя, проверяют наличие учебных принадлежностей
|
| Актуализация опорных знаний
| -сообщение о работе -раздача заданий на слайдах в проекторе (устный опрос) -сообщение критерии | отвечают на вопросы |
| Мотивация (актуализация субъектного опыта обучающихся) | учитель на слайде показывает несколько уравнений и решения этих уравнений | слушают учителя и называют тему урока |
| Изучение нового материала
| учитель объясняет новый материал приложение №1. | слушают учителя, задают вопросы, решают совместно |
| Закрепление полученных знаний | объяснить задания, озвучить критерии оценок Выполняют задания: приложение №2. | выполняют задания |
| Подведение итогов урока, рефлексия
| Подведение итогов урока, проверка учебной работы на уроке. Для рефлексии: Н а уроке было комфортно и все понятно - а уроке было комфортно и все понятно - Н а уроке немного затруднялся, не все понятно – а уроке немного затруднялся, не все понятно – Н а уроке было трудно, ничего не понял - а уроке было трудно, ничего не понял - | Слушают свои оценки |
| Домашнее задание | дает задание на дом: выучить конспект, подготовится тестовому контролю
| Записывают д/з |
Приложение №1
| Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня или знаком возведения в дробную степень. |
Для того, чтобы решить иррациональное уравнение, необходимо:
Уединить одно из выражений с корнем в одной части и избавиться от знака корня (возвести в соответствующую степень обе части уравнения и упростить его), повторять эту процедуру, пока все корни не уйдут или пока решение не станет очевидным;
Решить получившееся рациональное уравнение;
Для проверки подставить получившиеся корни уравнения в исходное уравнение.
Примеры:
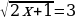
Избавляемся от корней. Поскольку корень второй степени, то обе части уравнения возводим в квадрат и упрощаем:
2х+1=9
Решаем полученное уравнение
2х=9-1
2х=8
х=4
проверка: подставляя вместо х=4 получим верное равенство.
Ответ : 4
Решая иррациональное уравнение, обязательно надо проводить проверку полученных корней!
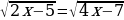
Как и раньше возводим в квадрат обе части:
2х-5=4х-7
Решаем уравнение
2х-4х=5-7
-2х=-2
х=1
Проверка, подставим 1 в исходное уравнение: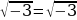
Вот это да! Ничего тебя тут не смущает?
Под квадратным корнем у нас отрицательное число!
Как же так вышло?
А это говорит о том, что это посторонний корень для исходного уравнения.
Да, это корень уравнения 2x−5=4x−7, но оно-то не исходное, его мы получили после преобразований!
В ответе пишем «нет решения».
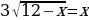
После возведения обеих частей в квадрат имеем:
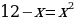 , упрощаем и решаем квадратное уравнение по теореме Виета
, упрощаем и решаем квадратное уравнение по теореме Виета
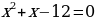
Х1=3
Х2=-4
У нас два корня, пробуем их подставить в исходное для проверки.
Подставляем 3, √9=3, 3=3 – подходит.
Подставим −4, получим √16=−4 не подходит
Но ведь 4≠−4! Что же получается, −4 – посторонний корень.
получается и в нашем примере с иррациональным уравнением, в результате преобразования мы можем найти все корни, но могут примешаться и посторонние.
Их надо отфильтровать проверкой, проверив, будет ли соблюдаться равенство исходного уравнения при их подстановке.
Если показатель степени четный, т.е. мы берем корень квадратный или корень 4 степени и т.д.;
Если подкоренное выражение отрицательно, то корень не имеет смысла (не существует);
Если подкоренное выражение равно нулю, то корень тоже равен нулю;
Если подкоренное выражение положительно, то значение корня существует и положительно.
Если показатель степени нечетный ( √3 √5...), то корни определены при любом значении подкоренного выражения.
При этом корень отрицателен, если подкоренное выражение отрицательно; равен нулю, если подкоренное выражение равно нулю; положителен, если покоренное выражение положительно.
Приложение №2.
Выполните упражнения
№1. Решите иррациональные уравнения:
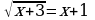
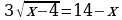
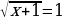

5







 а уроке было комфортно и все понятно -
а уроке было комфортно и все понятно -  а уроке немного затруднялся, не все понятно –
а уроке немного затруднялся, не все понятно –  а уроке было трудно, ничего не понял -
а уроке было трудно, ничего не понял - 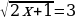
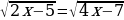
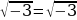
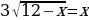
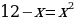 , упрощаем и решаем квадратное уравнение по теореме Виета
, упрощаем и решаем квадратное уравнение по теореме Виета