Урок «Линейная функция, ее график и свойства» (7 класс, учебник А.Г Мерзляк, В.Б. Полонский, М.С. Якир)
| Организационная структура урока |
| Этап урока | Содержание деятельности учителя | Содержание деятельности обучающегося
(осуществляемые действия) | Формируемые способы
деятельности |
| I. Организационный момент | Приветствие. Проверка готовности обучающихся к уроку. Создание в классе атмосферы психологического комфорта. – Давайте поможем друг другу настроиться на учебную деятельность! | Настраиваются на учебную деятельность. Концентрируют внимание на работе на уроке.
| Формирование навыков самоорганизации |
| II. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | Предлагает определить, что они уже знают и умеют, а что еще не становилось объектом их исследований.
Вопрос запуска постановки учебной задачи: – Можете ли вы пояснить, что такое линейная функция? Формулирует учебную задачу: – Исследовать линейную функцию | Заполняют таблицу. | Объекты для рассмотрения | Знаю (+) / Не знаю (–) | | Область определения функции | + | | Область значений функции | + | | Табличный способ задания функции | + | | График функции | + | | Линейная функция | – | Осознают важность решения поставленной учебной задачи | Умение развивать навыки целеполагания |
| III. Сообщение темы. Постановка цели и задач урока | Сообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока. – Внимательно прочитайте тему урока. – Что от вас ожидается на уроке? – Какие цели и задачи вы можете перед собой поставить? | Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока: – усвоить суть понятия «линейная функция»; – научиться строить графики линейной функции | Умение принимать и сохранять учебную задачу |
| IV. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов: – Насколько мне интересно исследовать линейные функции? – Получаю ли я удовольствие от процесса изучения алгебры? – Почему мне важно разобраться с понятием «линейная функция»? – Какова моя цель на данном уроке? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Умение выражать свои мысли. Развитие навыков самомотивации |
| V. Создание ситуации затруднения. Работа над темой урока | Организует обсуждение проблемного вопроса: – Какие функции изображены на иллюстрации? – Что их объединяет? –Может ли у них быть общее название? 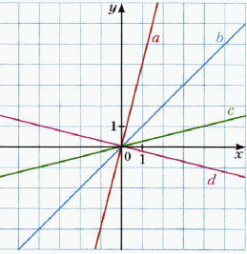
Организует анализ определения понятия «линейная функция». Предлагает рассмотреть и проанализировать примеры линейных функций: 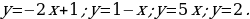
Предлагает выяснить, как выглядят графики линейных функций.
Объясняет, что линейную функцию, которую задают формулой 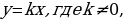 называют прямой пропорциональностью. называют прямой пропорциональностью. Примеры прямых пропорциональностей: 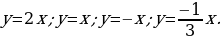
– В начале урока вы видели именно линейные функции прямой пропорциональности | Принимают участие в обсуждении проблемных вопросов. Испытывают определенные трудности при ответе на вопрос. Выбирают, как организовать свою работу на уроке по изучению нового материала: А) буду самостоятельно изучать новый материал; Б) буду работать в паре; В) буду работать в группе.
Анализируют определение. Заполняют таблицу. | Определение | Мне непонятно… | Вопросы учителю | | Функцию, которую можно задать формулой вида 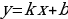 , где , где 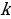 и и 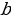 – некоторые числа, – некоторые числа, х – независимая переменная, называют линейной | Нужно уточнить… | Почему…? | Делают записи в тетради. Задают вопросы
| Умение выражать свои мысли в соответствии с задачей.
|
| VI. Закрепление изученного материала | Организует самоанализ усвоенных учащимися знаний. Оказывает помощь ученикам, которые не знают ответов на вопросы. Создает условия для дополнительного изучения вопросов, которые вызвали затруднения | Отвечают на вопросы. Определяют свой уровень усвоения знаний. Заполняют таблицу. | Вопросы | Варианты ответов | | Знаю ответ на вопрос (+) | Не знаю ответ на вопрос (+) | | Какую функцию называют линейной? |
|
| | Что является графиком линейной функции? |
|
| | Какую функцию называют прямой пропорциональностью? |
|
| | Что является графиком прямой пропорциональности? |
|
| | Графиком какой функции является ось абсцисс? |
|
| Анализируют ответы на вопросы. Проводят дополнительное изучение нового материала. Задают вопросы учителю | Умение осуществлять актуализацию полученных знаний и умений
|
| VII. Решение заданий | Задания: 1. (№ 849) Является ли линейной функция, заданная формулой: 1) 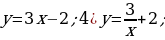 2) 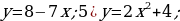 3) 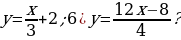 2. (№ 850) Является ли прямой пропорциональностью функция, заданная формулой: 1) 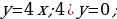 2) 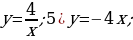 3) 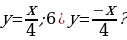 3. (№ 851) Линейная функция задана формулой 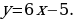 Заполните таблицу. Заполните таблицу.
| Решение. 1. 1) линейная; 4) не линейная; 2) линейная; 5) не линейная; 3) линейная; 6) линейная.
2. 1) является; 4) не является; 2) не является; 5) является; 3) является; 6) является.
3. | х | –3 | –2 | –1 | 0 | 1 | 2 | 3 | | у | –23 | –17 | –11 | –5 | 1 | 7 | 13 |
| Умение самостоятельно принимать решения |
| VIII. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами: – Что нового я узнал на уроке? – Что я не до конца понял из нового материала? – Достиг ли я поставленных целей и задач урока? – Что помешало мне на уроке работать еще лучше? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию. | Умение отслеживать цель учебной деятельности |
| IX. Домашнее задание | Помогает учащимся выбрать задания из учебника. Обращает внимание на возможности и способности учащихся | Выбирают задания, которые будут решать дома. Записывают домашнее задание. | Формирование навыков самоорганизации |








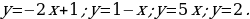
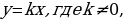 называют прямой пропорциональностью.
называют прямой пропорциональностью.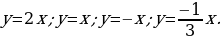
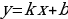 , где
, где 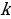 и
и 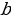 – некоторые числа,
– некоторые числа, 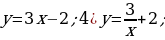
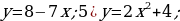
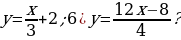
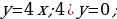
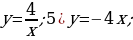
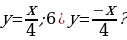
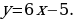 Заполните таблицу.
Заполните таблицу.









