Технологическая карта урока "Первый признак равенства треугольников" (7 класс, учебник Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.)

Цели деятельности

учителя

Создать условия для разъяснения смысла слов «теорема» и «доказательство теоремы», формулировки и доказательства первого признака равенства треугольников

Термины и понятия

Треугольник, угол между двумя сторонами, теорема, признак

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира; приобретают навыки геометрических построений

Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки.

Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Геометрия. 7 – 9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. – М.: Просвещение, 2023.

• Задания для самостоятельной и фронтальной работы

I этап. Актуализация знаний учащихся

Цель деятельности

Совместная деятельность

Систематизировать знания учащихся по теории

(Ф/И)

1. Обсуждение вопросов учащихся по домашнему заданию.

2. Повторение теории.

1) Повторить определение смежных углов и их свойство.

2) Повторить определение вертикальных углов и их свойство.

3) Вспомнить определение равных фигур, биссектрисы угла.

4) Вспомнить, какой угол называется острым, прямым, тупым.

5) Повторить определение треугольника, его элементов; определение периметра треугольника; определение равных треугольников

II этап. Мотивация к деятельности

Цель деятельности

Задания для самостоятельной работы

Совершенствовать навыки решения задач по готовым чертежам

(И)

III этап. Изучение новой темы

Цель деятельности

Совместная деятельность

Вывести первый признак равенства треугольников

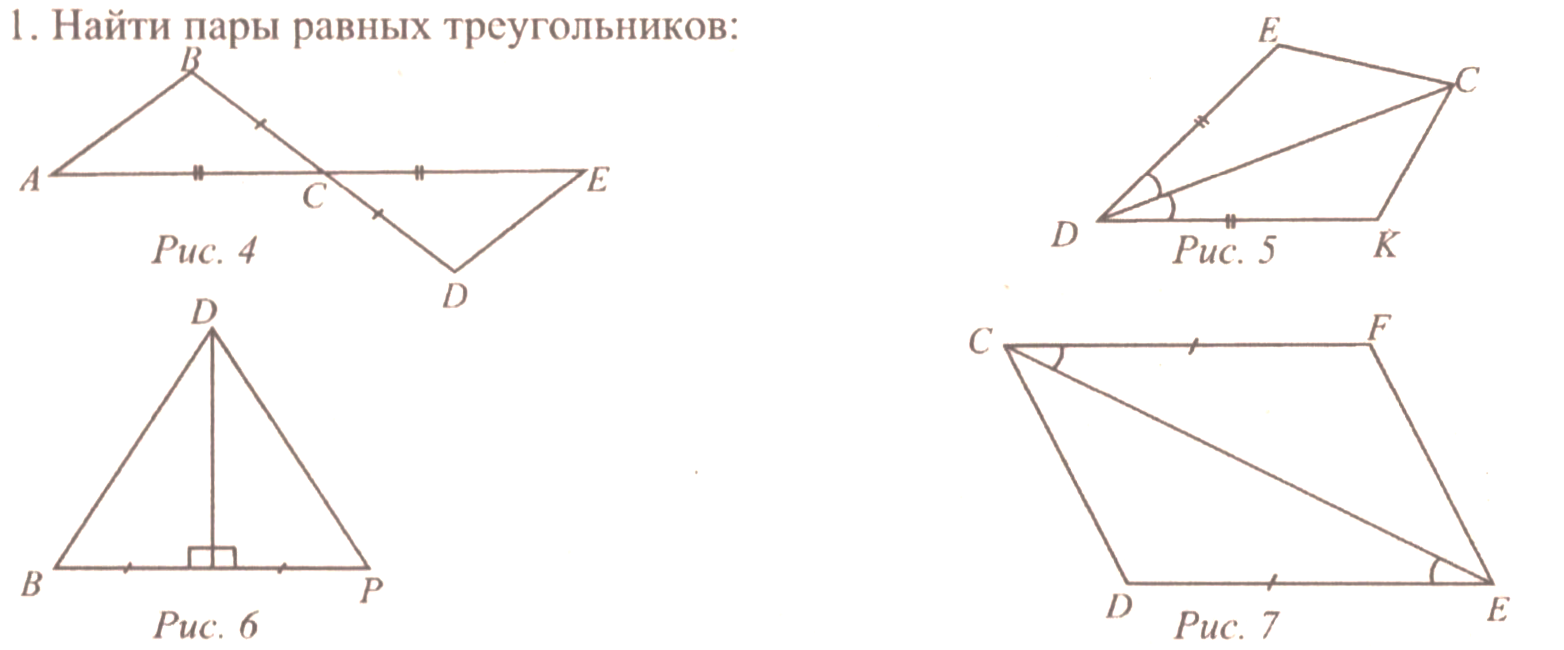
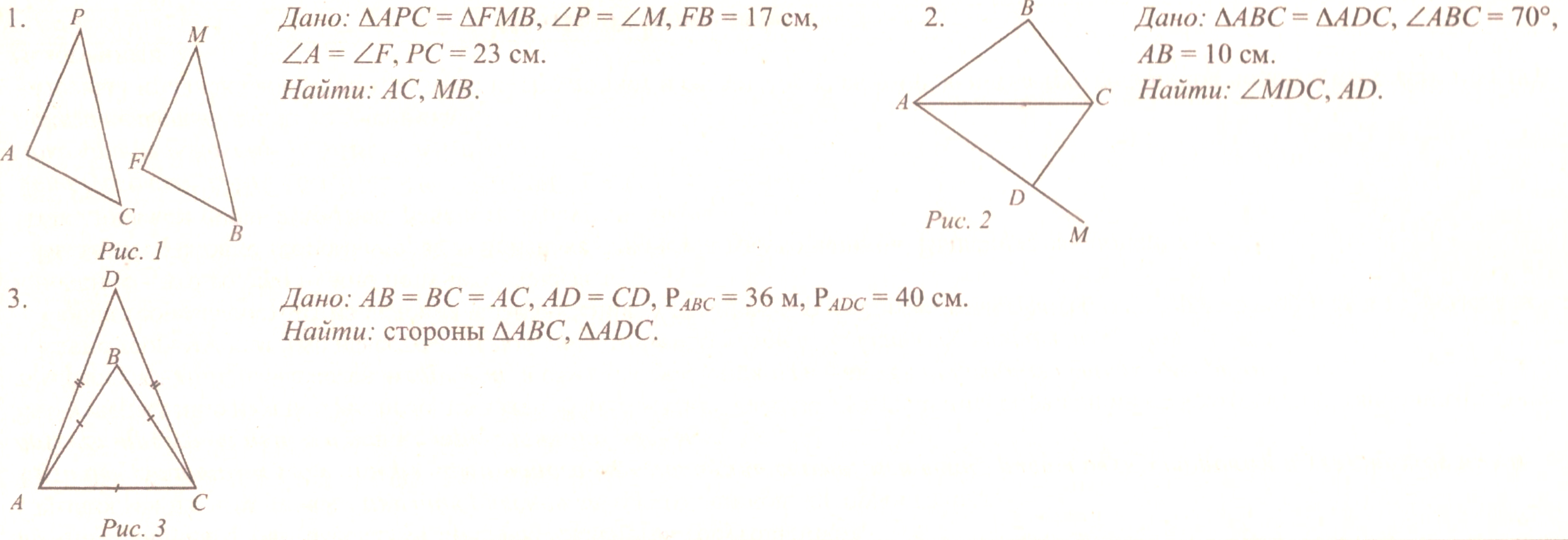(Ф) Изучение темы осуществляется в форме беседы учителя с учащимися; теорему лучше доказать самому учителю.

– Какие условия должны выполняться для того, чтобы АВС был равен А₁В₁С₁? (АВ = А₁В₁, АС = А₁С₁, ВС = В₁С₁,

А = А₁, В = В₁, С = С₁.)

– Нельзя ли уменьшить количество условий для доказательства равенства двух треугольников? (Учащиеся высказывают свои предположения.)

– Оказывается, не нужно проверять равенство всех сторон и углов одного треугольника сторонам и углам другого треугольника. Достаточно сравнить лишь три элемента одного треугольника с тремя элементами другого. О том, какие именно элементы нужно сравнивать, нам расскажут признаки равенства треугольников.

Сегодня мы изучим первый признак равенства треугольников, который гласит:

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Это утверждение нам необходимо доказать. В математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы.

– Какие теоремы нам уже известны? (Свойство смежных углов и свойство вертикальных углов.)

– Любая теорема состоит из условия и заключения. Условие – это уже известные факты, о которых говорится в теореме, а заключение – это то, что нужно получить, доказать.

– Выделите условие теоремы первого признака равенства треугольников. Выделите заключение.

Итак, докажем первый признак равенства треугольников:

Дано (условие): АВС, А₁В₁С₁, АВ = А₁В₁, АС = А₁С₁, А = А₁.

Доказать (заключение): АВС = А₁В₁С₁.

Доказательство: см. п. 15 учебника.

– Первый признак равенства треугольников удобнее называть признаком равенства треугольников по двум сторонам и углу между ними

IV этап. Решение задач

Цель деятельности

Задания для самостоятельной работы

Совершенствовать навыки в решении задач на изученную тему

(Ф/И)

2. Решить задачи № 101 и 102 на доске и в тетрадях

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

– Что нового узнали на уроке?

– Что такое теорема? Из чего она состоит?

(И) Домашнее задание: знать доказательство первого признака равенства треугольников (п.15), решить задачи № 98, 99, 100