| 4. Закрепление изученного материала | Итак, вы вспомнили определение параллельного переноса, его основные свойства, а так же повторили, как построить точку и отрезок параллельным переносом на заданный вектор. Теперь можем приступить к решению задач.
Откройте учебник на странице 302, номер задачи 1164. К доске пойдет Кирилл. Кирилл, прочитай условие задачи. Ты выполняешь задание под буквой а).
О чем говорится в задаче? Как расположена точка 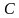 относительно точки относительно точки 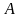 и и 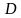 ? ? Верно. Запишите условие задачи, постройте чертеж.
Предлагаю обозначить вектор  . .
Кирилл, как ты думаешь, что необходимо сделать, что бы построить точку  ? ?
Спасибо, Кирилл, всё верно, молодец! Присаживайся.
Под буквой б) задание выполнит Лёша, выходи к доске.
Что нам нужно доказать, чтобы фигура  являлась трапецией? являлась трапецией?
Хорошо, а как доказать, что полученная трапеция является равнобедренной?
Верно, что ты можешь сказать об отрезках  ? ?
Хорошо, а об отрезках  ? ?
Какой вывод можно сделать?
Верно. По условию дан равнобедренный треугольник, значит, что можно сказать о его боковых сторонах? Да, теперь посмотри на 3 и 6 пункт, что ты можешь сказать? Если  , то как будут расположены отрезки , то как будут расположены отрезки  и и  ? ? Какой вывод можно сделать из пунктов 1, 2 и 8? Хорошо, а теперь посмотри на все пункты доказательства и сделай заключительный вывод.
Молодец, Лёша, цель достигнута, присаживайся на место.
А сейчас обсудим задачу под номером 1178 на странице 304, которая будет являться вашим домашним заданием. Саша, прочитай условие задачи.
Ответьте, о каких геометрических фигурах говориться в задачи, Катя?
Что требуется оказать в задаче, Данил? Рассмотрите чертёж, что вы можете сказать о сторонах квадратов  , Вера? , Вера?
Хорошо, а теперь обратите внимание на диагонали квадратов  и и  . Как они расположены по отношению друг к другу, Миша? . Как они расположены по отношению друг к другу, Миша? А что ты можешь тогда сказать о половинах этих диагоналей  и и  ? ?
Верно, вы уже устно доказали, что  и и параллельны и равны, а в задаче требуется доказать, что параллельны и равны, а в задаче требуется доказать, что  , значит какую фигуру можно рассмотреть, Женя, назови? , значит какую фигуру можно рассмотреть, Женя, назови? Делаю вам подсказку: если вы докажите, что фигура  – параллелограмм, то задача будет решена. Дома вы подумаете над доказательством и оформлением доказательства. – параллелограмм, то задача будет решена. Дома вы подумаете над доказательством и оформлением доказательства. |
Открывают учебник.
Кирилл: «Даны равнобедренный треугольник  с основанием с основанием  и точка и точка 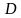 на прямой на прямой  , такая, что точка , такая, что точка 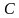 лежит на отрезке лежит на отрезке  . . а) Постройте отрезок  , который получается из отрезка , который получается из отрезка  параллельным переносом на вектор параллельным переносом на вектор  . б) Докажите, что четырехугольник . б) Докажите, что четырехугольник  – равнобедренная трапеция». – равнобедренная трапеция».
Кирилл: «О равнобедренном треугольнике. Точка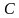 лежит между точками лежит между точками 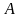 и и 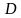 ». ».
Кирилл: «Дано: а) построить: при перенос на при перенос на 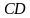 . . Построение: 1. От точки  отложим вектор отложим вектор  ; ; 2. Соединим точку  и и 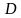 3.  – искомый». – искомый».
Лёша: «Доказать:  – равнобедренная трапеция. – равнобедренная трапеция.
Чтобы доказать, что фигура  – трапеция, необходимо доказать, что – трапеция, необходимо доказать, что
 . .
Для этого нужно доказать, что  . .
1.  (по построению). (по построению). 2.  (по определению параллельного переноса). (по определению параллельного переноса). 3.  (по свойству параллельного переноса). (по свойству параллельного переноса). 4.  (по определению параллельного переноса). (по определению параллельного переноса). 5. Из (1), (2), (3), (4) –  – параллелограмм (по определению параллелограмма). – параллелограмм (по определению параллелограмма). Что и требовалось доказать».
6.  (по условию). (по условию).
7. Из (3), (6) –  . .
8.  (по построению). (по построению).
9. Из (1), (2), (8) –  не параллелен не параллелен  . .
10. Из (7), (8), (9) –  – равнобедренная трапеция. – равнобедренная трапеция. Что и требовалось доказать».
Саша: «На сторонах  и и 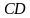 параллелограмма параллелограмма  построены квадраты так, как показано на рисунке 332. Используя параллельный перенос, докажите, что отрезок, соединяющий центры этих квадратов, равен и параллелен стороне построены квадраты так, как показано на рисунке 332. Используя параллельный перенос, докажите, что отрезок, соединяющий центры этих квадратов, равен и параллелен стороне  ». ».
Катя: «В задачи говориться о двух квадратах  и и  , а так же о параллелограмме , а так же о параллелограмме  ». ».
Данил: «Доказать:  ». ».
Вера: «Данные стороны равны и параллельны по построению, поскольку по условию». по условию».
Миша: «Диагонали расположены параллельно.
Диагонали так же будут равны друг другу и параллельны».
Женя: « ». ».
|
Познавательные: извлечение из текстов математической информации, структурирование знаний, выбор способов решения задач, анализ объектов и синтез.
Построение логической цепи рассуждений.
Регулятивные: планирование пути достижения цели; прогнозирование.
Коммуникативные: развитие умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействия.
Личностные: осознание ответственности за общее дело.
Познавательные: осознанное и произвольное построение речевого высказывания.
Коммуникативные: выражение своих мыслей с достаточной полнотой и точностью, формирование и аргументация своего мнения в коммуникации. |







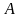 , отрезок
, отрезок 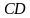 и вектор
и вектор 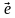 . Начертите у себя в тетрадях данные геометрические объекты.
. Начертите у себя в тетрадях данные геометрические объекты.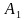 , отрезок
, отрезок 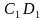 , которые получаются из точки
, которые получаются из точки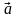 называется отображение плоскости на себя, при котором каждая точка
называется отображение плоскости на себя, при котором каждая точка 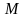 отображается в такую точку
отображается в такую точку 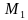 , что вектор
, что вектор 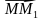 равен вектору
равен вектору  отложить вектор, равный вектору
отложить вектор, равный вектору  отложить вектор, равный вектору
отложить вектор, равный вектору 









