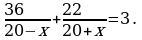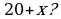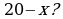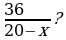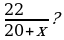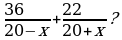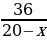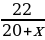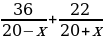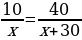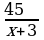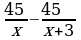Технологическая карта урока "Решение текстовых задач с помощью дробно-рациональных уравнений"

Тема урока

Решение текстовых задач с помощью дробно-рациональных уравнений

Цель урока

Обучающая:

Закрепить умения: решать дробно-рациональные уравнения, составлять дробно-рациональные уравнения по условию задачи, определять, соответствуют ли найденные корни уравнения условию задачи;

Развивающая:

развитие умения правильно оперировать полученными знаниями, логически мыслить;

развитие интеллектуальных умений;

развитие умения принимать решения.

Воспитательная:

воспитание познавательного интереса к предмету;

воспитание самостоятельности при решении учебных задач;

воспитание воли и упорства для достижения конечных результатов.

Основное содержание темы, термины и понятия

Решение дробно-рациональных уравнений. Решение задач, с помощью дробно-рациональных уравнений.

Личностные

Метапредметные

Предметные

-самоопределение, и смыслообразование;

-умение приводить примеры;

-находчивость и активность при решении задач;

-умение видеть математическую задачу в контексте проблемной ситуации и других дисциплинах, в окружающей жизни;

-находить в различных источниках информацию, необходимую для решения математической проблемы;

-продолжить работу с квадратными уравнениями;

-умение работать с математическим текстом;

-грамотно использовать математическую терминологию и символику.

Организация пространства: учебный кабинет

Тип урока

Методы работы

Ресурсы

комбинированный

По источникам знаний: словесные, наглядные.

По степени взаимодействия учитель-ученик: эвристическая беседа.

Относительно характера познавательной деятельности: репродуктивный, частично-поисковый.

Презентация, карточки

Этапы урока

Задачи этапа

Деятельность учителя

Деятельность учащихся

УУД

1. Организационный момент

2. Проверка д/з

Создать благоприятный психологический настрой на работу

Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.

Здравствуйте, ребята.

Эпиграфом урока на сегодня, я выбрала слова математика, педагога, книговеда Алексея Ивановича Маркушевича

«Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и открытий»

- Есть ли вопросы по д/з?

Сегодня мы рассмотрим решение задачи, решение которой сводится к дробно-рациональным уравнениям.

Мотивация (самоопределение) к учебной деятельности.

Включаются в деловой ритм урока.

Личностные: самоопределение.

Регулятивные: целеполагание.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

3.Актуализация знаний

4. Решение дробно-рациональных уравнений

Актуализация опорных знаний и способов действий.

Фронтальный опрос, устная работа с классом.

Выполните следующие задания:

Решите уравнение, составьте устный алгоритм решения дробно-рационального уравнения

На экране появляются слайды 2 и 3 с заданиями для устной работы.

1. Катер, развивающий в стоячей воде скорость 20 км/ч, прошел 36 км против течения и 22 км по течению, затратив на весь путь 3 часа. Найдите скорость течения реки.

Для решения этой задачи составлено уравнение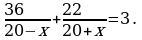

Ответить на вопросы:

- Что принято за х?

- Что выражается суммой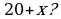

- Что выражается разностью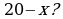

- Что выражается дробью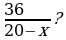

- Что выражается дробью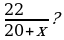

- Что выражается суммой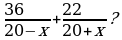

2. Расстояние между двумя населенными пунктами 50 км. Из этих пунктов одновременно навстречу друг другу выехали мотоциклист и велосипедист. Скорость мотоциклиста на 30 км/ч больше. Встретились они на расстоянии 10 км от одного из населенных пунктов. Какова скорость велосипедиста?

Составьте уравнение для решения задачи.

Называют дробно-рациональные уравнения

Решают уравнение у доски с объяснением.

Рассказывают алгоритм решения рациональных уравнений.

Отвечают на поставленные вопросы.

За х принята скорость течения реки.

Скорость катера по течению реки выражается суммой

20 + х.

Скорость катера против течения реки выражается

разностью 20 – х.

Дробью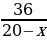

выражается время движения катера против течения реки.

Дробью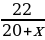

Выражается время движения катера по течению реки.

Суммой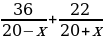

выражается время, затраченное на весь путь.

Скорость велосипедиста х км/ч.

Для решения задачи составим уравнение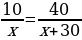

На этапе идёт повторение изученного материала, и выявление затруднений в индивидуальной деятельности каждого учащегося. Формируются регулятивные УУД.

5. Выполнение контролирующего задания по изученной теме и включение в систему знаний повторения

6.Физминутка

Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков.

Выполнение тестового задания.

Два велосипедиста одновременно выехали из села в город, расстояние между которыми 45 км. Скорость первого велосипедиста на 3 км/ч больше скорости второго, поэтому он прибыл в город на 30 минут раньше. Найти скорость каждого велосипедиста.

1) Заполнить ячейки таблицы.

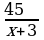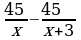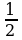2) Составить и записать уравнение по условию задачи:

___________________________________.

Учащиеся выполняют задание в распечатанных тестах

Учатся находить информацию в тексте задачи, выделять главное, применять знания.

Самопроверка.

Выполняют движения (видеоролик)

Регулятивные: целеполагание.

Коммуникативные: постановка вопросов.

Познавательные: самостоятельное выделение-формулирование познавательной цели; логические - формулирование проблемы.

На данном этапе предлагаются задания, при решении которых используется ранее изученный материал. Выполняются универсальные логические действия: анализ, синтез.

7.Выполнение заданий в группах.

Установление правильности и осознанности изучения темы.

Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу.

1.Исторический материал

(слайд 10-11)

2. Каждая группа оформляет решение задачи на листе.

1 группа:

Катер прошел 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему понадобилось бы, если бы он шел 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч?

2 группа:

Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В?

Затем к доске вызываются по два ученика, чтобы объяснить решение задачи.

При составлении уравнения удобно пользоваться таблицей.

Учитель контролирует выполнение задания, отвечает на возникшие вопросы, оказывает помощь слабоуспевающим ученикам.

Учащийся читает сообщение:

Уже около 4000 лед назад вавилоняне и египтяне решали разные задачи землемерия, строительства и военного дела с помощью уравнений. Такие задачи встречаются во многих текстах глубокой древности. В Московском папирусе, представляющем свиток, изготовленный из растений, неизвестное имеет особый символ и название: «хау» или «аха». Оно означает «количество», «куча». Так называемое исчисление «кучи» приблизительно соответствует нашему решению задач с помощью уравнений.

Работают в группах, обсуждают решение задачи.

Учатся доносить свою позицию до других (строить высказывания, пользуясь математической терминологией), слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения, при необходимости отстаивать свою точку зрения, аргументировать её.

Формирование умений в использовании опорной схемы для решения задач.

Регулятивные: контроль, оценка, коррекция.

Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия.

Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера.

8. Подготовка к ОГЭ

Выявление качества и уровня усвоения знаний по заданиям ОГЭ, повторение изученного.

(Слайд 12-13)

Решение с устным объяснением

Выполняются универсальные логические действия: анализ, синтез.

9. Подведение итогов урока.

Дать качественную оценку работы класса и отдельных обучаемых

- Чему учились сегодня на уроке?

-Что повторяли?

Оценить отдельных учащихся

Решали задачи с помощью составления дробно-рациональных уравнений

Регулятивные: оценка-осознание уровня и качества усвоения; контроль.

10. Информация о домашнем задании

Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.

Прочитать п.4.6 учебника, повторить алгоритмы решения задач с помощью уравнений.

Решить задачи по карточкам (Приложение 2)

Составить и решить задачу с подобными данными (для сильных учащихся)

Д/з включает в себя как репродуктивное задание, так и творческое, что позволяет вызвать у детей познавательный интерес. Формируются познавательные УУД,

8. Рефлексия

Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.

Если вы считаете, что поняли тему урока, то нарисуйте на полях тетради смайлик

Если вы считаете, что не достаточно усвоили материал, то

Если вы считаете, что не поняли тему урока, то

Учатся определять степень успешности выполнения своей работы, осознание своей УД. Понимать причины своего неуспеха и находить способы выхода из этой ситуации

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;

Познавательные: рефлексия.