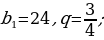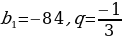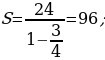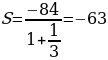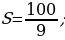Урок «Сумма бесконечной геометрической прогрессии, у которой модуль знаменателя меньше 1» (9 класс, учебник А.Г Мерзляк, В.Б. Полонский, М.С. Якир)
| Организационная структура урока |
| Этап урока | Содержание деятельности учителя | Содержание деятельности обучающегося
(осуществляемые действия) | Формируемые способы
деятельности |
| I. Организационный момент | Приветствие. Проверка готовности обучающихся к уроку. Создание в классе атмосферы психологического комфорта. – Предлагаю начать урок с улыбки! – Пожелаем друг другу плодотворной работы на уроке! | Настраиваются на учебную деятельность. Концентрируют внимание на работе на уроке.
| Формирование навыков самоорганизации |
| II. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | Предлагает обучающимся определить свои достижения и трудности в изучении геометрической прогрессии.
Вопрос запуска постановки учебной задачи: – Достаточно ли у вас знаний для нахождения суммы членов бесконечной геометрической прогрессии? Формулирует учебную задачу: – Исследовать формулу нахождения суммы членов бесконечной геометрической прогрессии | Заполняют таблицу. | Мои достижения | Мои трудности | |
|
| Осознают важность решения поставленной учебной задачи | Развитие навыков целеполагания |
| III. Сообщение темы. Постановка цели и задач урока | Сообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока. – Внимательно прочитайте тему урока. – Что от вас ожидается на уроке? – Какие цели и задачи вы можете перед собой поставить? | Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока: – узнать формулу для нахождения суммы членов бесконечной геометрической прогрессии; – научиться находить сумму членов бесконечной геометрической прогрессии | Умение принимать и сохранять учебную задачу |
| IV. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов. – Насколько мне понятны поставленные задачи урока? – Почему я заинтересован в выполнении поставленных целей и задач урока? – Как я должен относиться к урокам алгебры? – Какова моя личная цель на данном уроке? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Умение выражать свои мысли, демонстрировать самомотивацию |
| V. Создание ситуации затруднения. Работа над темой урока | Организует обсуждение проблемного вопроса: – Как можно найти сумму бесконечного числа слагаемых на примере иллюстрации? 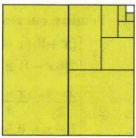
Организует исследование формулы: 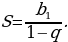
Организует анализ решенного задания: Задание 1. Представьте бесконечную десятичную дробь 0,2(54) в виде обыкновенной дроби.
Предлагает обучающимся попробовать самостоятельно решить задание, а потом сравнить свое решение с решением из учебника. Задание 2. Дан правильный треугольник со стороной а. Из высот этого треугольника построен второй правильный треугольник, из высот второго построен третий треугольник и т.д. Найдите сумму периметров и сумму площадей всех треугольников
| Принимают участие в обсуждении проблемного вопроса. Предлагают свои гипотезы. Проводят необходимые дополнительные исследования. Находят и анализируют формулу 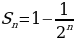
Проводят исследование. Работают с источниками информации. Заполняют таблицу. | Объект исследования | Вопросы для исследований | Вопросы учителю | | 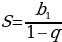
| Для чего нужна данная формула? Как была получена данная формула? Что такое S? Что такое 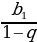 | Почему…?
Каким образом…? | Анализируют решение задания. Выявляют логику решения задания. Формулируют вопросы учителю. Заполняют таблицу. | Решение задания | Мне непонятно… | Вопросы учителю | | 0,2(54) = 0,2545454… = 0,2 + + 0,0545454…= 0,2 + 0,054 + 0,00054 + 0,0000054 + … |
| Почему…? | | Бесконечную периодическую десятичную дробь 0,0545454… можно рассматривать как сумму бесконечной геометрической прогрессии, первый член которой равен 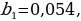 а знаменатель а знаменатель 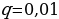 |
| Каким образом…? | | 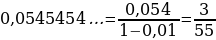
|
| Как…? | | 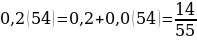
|
| Зачем…? | Решают задание. Делают сравнение собственного решения с решением из учебника. | Решение задания из учебника | Комментарий обучающихся | | Высота правильного треугольника со стороной а равна 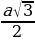 |
| | Высота правильного треугольника со стороной 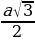 равна равна 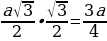 и т.д. и т.д. |
| | Тогда периметры образуют последовательность 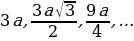 , являющуюся геометрической прогрессией со знаменателем , являющуюся геометрической прогрессией со знаменателем 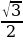 , меньшим 1. , меньшим 1. 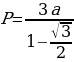
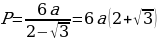
|
| | 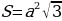
|
|
| Умение выражать свои мысли в соответствии с задачей. Умение анализировать информацию
|
| VI. Закрепление изученного материала | Организует самоанализ усвоенных учащимися знаний. Оказывает помощь ученикам, которые не знают ответов на вопросы. Создает условия для дополнительного изучения вопросов, которые вызвали затруднения
| Отвечают на вопросы. Определяют свой уровень усвоения знаний. Заполняют таблицу. | Вопросы | Варианты ответов | | Знаю ответ на вопрос (+) | Не знаю ответ на вопрос (+) | | Как называют число 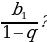 |
|
| | Что означает запись 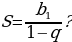 |
|
| | Что называют суммой бесконечной геометрической прогрессии, модуль знаменателя которой меньше единицы? |
|
| Анализируют ответы на вопросы. Проводят дополнительное Изучение нового материала. Задают вопросы учителю | Умение осуществлять актуализацию полученных на уроке знаний и умений |
| VII. Решение заданий | Задания: 1. (№ 896) Найдите сумму бесконечной геометрической прогрессии (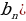 со знаменателем q, если: со знаменателем q, если: 1) 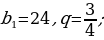
2) 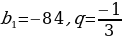
2. (№ 898) Найдите сумму бесконечной геометрической прогрессии: 1) 10; 1; 0,1; …; 2) 0,3; 0,03; 0,003; …
| Решения. 1.
1) 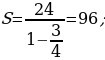
2) 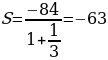 2.
1) 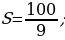 2) 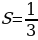 | Умение самостоятельно принимать решения |
| VIII. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами. – Каковы мои достижения на уроке? – Что нового я узнал? – Нужна ли мне помощь учителя? – Достиг ли я поставленных целей и задач урока? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию. | Умение отслеживать цель учебной деятельности |
| IХ. Домашнее задание | Помогает учащимся выбрать задания из учебника. Обращает внимание на возможности и способности обучающихся | Выбирают задания, которые будут решать дома. Записывают домашнее задание. | Формирование навыков самоорганизации |








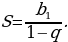
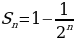
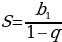
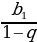
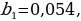 а знаменатель
а знаменатель 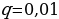
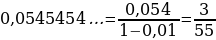
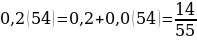
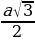
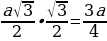 и т.д.
и т.д.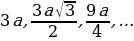 , являющуюся геометрической прогрессией со знаменателем
, являющуюся геометрической прогрессией со знаменателем 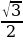 , меньшим 1.
, меньшим 1.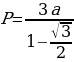
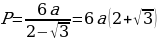
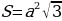
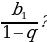
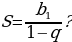
 со знаменателем q, если:
со знаменателем q, если: