Технологическая карта урока «Теорема Фалеса. Теорема о пропорциональных отрезках» (8 класс, учебник А.Г Мерзляк, В.Б. Полонский, М.С. Якир)

Тип урока: урок постановки учебной задачи

Задачи: обеспечить усвоение знаний о теореме Фалеса и о теореме о пропорциональных отрезках; формировать умения доказывать и применять теоремы

Планируемые результаты

Предметные:

Научатся доказывать и применять теорему Фалеса и ее обобщение, теорему о пропорциональных отрезках, свойства медиан треугольника и биссектрисы треугольника

Метапредметные:

Познавательные – управлять своей познавательной и учебной деятельностью посредством постановки целей, планирования, контроля.

Регулятивные – оценивать достигнутый результат учебной деятельности.

Коммуникативные – регулировать собственную деятельность посредством письменной речи

Личностные:

Понимают необходимость математического образования, выраженную в преобладании учебно-познавательных мотивов

Организационная структура урока

Этап урока

Содержание деятельности учителя

Содержание деятельности обучающегося
(осуществляемые действия)

Формируемые способы
деятельности

I. Организационный момент

Приветствует обучающихся; проверяет их готовность к уроку. Создает в классе атмосферы психологического комфорта.

– Мне очень приятно обучать вас геометрии!

– Спасибо вам за ваши усилия!

– Вы замечательный класс!

Настраиваются на учебную деятельность.

Концентрируют внимание на работе во время урока.

Формирование навыков самоорганизации

II. Актуализация опорных знаний и жизненного опыта.

Постановка учебной задачи

Предлагает учащимся поделиться своими познаниями о треугольниках из курса геометрии в 7 классе.

Вопрос запуска постановки учебной задачи:

– Знаете ли вы теорему Фалеса и теорему о пропорциональных отрезках?

Формулирует учебную задачу:

– Исследовать теорему Фалеса и теорему о пропорциональных отрезках

Выступают перед классом или в группах.

– О треугольниках я знаю…

– Я выполнял задания…

– У меня получалось…

– Я преодолел такие трудности…

Осознают важность решения поставленной учебной задачи.

Развитие навыков целеполагания

III. Сообщение темы.

Постановка цели и задач урока

Сообщает тему урока.

Организует совместное с учащимися формулирование цели и задач урока.

– Внимательно прочитайте тему урока.

– Что от вас ожидается на уроке?

– Какие цели и задачи вы можете перед собой поставить?

Записывают в тетрадь тему урока.

Участвуют в формулировании целей и задач урока:

– усвоить суть теоремы Фалеса и теоремы о пропорциональных отрезках;

– научиться доказывать и применять теоремы

Умение принимать и сохранять учебную задачу

IV. Мотивирование к учебной деятельности

Способствует обсуждению мотивационных вопросов.

– Что меня заинтересовало в теме урока?

– Насколько для меня понятны задачи урока?

– Я готов сотрудничать с учителем для достижения целей и задач урока?

– Что отвлекает меня от изучения новой темы урока? Как решить эту проблему?

Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности.

Умение выражать свои мысли; развитие навыков самомотивации

V. Создание ситуации затруднения.

Работа над темой урока

Организует обсуждение проблемных вопросов:

– Как доказать теорему Фалеса: «Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне»?

– Что означает данный рисунок?

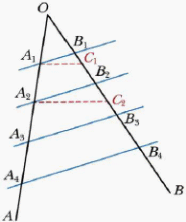
Предлагает проанализировать определение.

Отвечает на вопросы учащихся.

Организует исследование теоремы о пропорциональных отрезках.

О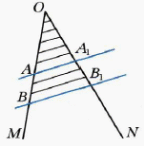 бращает внимание на чертежи:

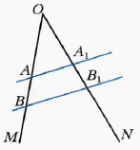
Организует исследование теорем. Отвечает на вопросы учащихся.

Стимулирует самостоятельную познавательную деятельность учащихся.

Организует совместный разбор решения задачи:

– Разделите данный отрезок на три равных отрезка.

Делает графическое изображение: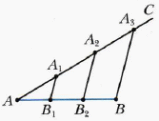

Принимают участие в обсуждении проблемных вопросов.

Затрудняются ответить на вопрос.

Проводят исследования.

Работают с источниками информации. Записывают в тетрадь доказательство теоремы Фалеса.

Обсуждают полученный результат.

Анализируют определение. Формулируют дополнительные вопросы учителю для выяснения неясных аспектов рассматриваемого определения.

Проводят исследование теоремы.

Находят и анализируют доказательство теоремы..

Проводят исследование теорем.

Предлагают свои идеи решения задания. Сверяют предложенные подходы с решением учителя.

Умение выражать свои мысли в соответствии с учебной задачей.

Умение анализировать информацию

VI. Закрепление изученного материала

Организует самоанализ усвоенных учащимися знаний.

Оказывает помощь ученикам, которые не знают ответов на вопросы.

Создает условия для дополнительного изучения вопросов, которые вызвали затруднения

Отвечают на вопросы. Определяют свой уровень усвоения знаний. Заполняют таблицу.

Анализируют ответы на вопросы. Проводят дополнительное изучение нового материала. Задают вопросы учителю

Умение осуществлять актуализацию полученных на уроке знаний и умений

VII. Решение заданий

Предлагает учащимся ознакомиться с заданиями, которые предстоит выполнить на уроке.

1. (№ 370) Начертите произвольный отрезок АВ и постройте на нем точку С такую, что АС : СВ = 2 : 7.

2. (№ 381) Докажите, что средняя линия треугольника АВС, параллельная стороне АС, делит пополам любой отрезок, соединяющий вершину В с произвольной точкой стороны АС

В

Е

Решение.

1. Проведем луч АК, который не лежит на прямой АВ. На луче АК от точки А отложим отрезок АК₁ произвольной длины. Потом от точки А последовательно отложим отрезки АС₁ и С₁В₁ такие, что АС₁ = 2АК₁, С₁В₁ = 7АК₁. Проведем отрезок В₁В и через точку С₁ проведем прямую, параллельную В₁В. Эта прямая пересекает АВ в точке С. По теореме Фалеса АС : СВ = АС₁ : С₁В₁, то есть АС : СВ = 2 : 7.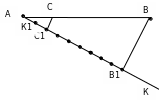

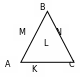
2. М – середина АВ, N – середина ВС, К – произвольная точка стороны АС, что не совпадает ни с А, ни с С. Тогда MN – средняя линия треугольника АВС, L – точка ее пересечения с ВК. MNАС, и они пересекают стороны угла АВК в точках М и А, L и К. На стороне ВА эти прямые отсекают равные отрезки

МВ = МА, тогда по теореме Фалеса они отсекают и на стороне ВК равные отрезки. Поэтому BL = LK. Так как точка К была выбрана произвольно, то средняя линия треугольника MN делит любой отрезок, что соединяет точку В с точкой К стороны АС, пополам. Доказано

Умение самостоятельно принимать решения

VIII. Подведение итогов урока. Рефлексия

Организует подведение итогов урока обучающимися.

Способствует размышлению учащихся над вопросами:

– У меня сегодня на уроке получилось…

– Мне стало понятно…

– Я научился…

– Мне было трудно…

– Я заинтересовался…

– Я хочу узнать больше о…

Подводят итоги своей работы на уроке.

Проводят самооценку, рефлексию.

Умение отслеживать цель учебной деятельности

IX. Домашнее задание

Помогает учащимся выбрать задания из учебника.

Обращает внимание на возможности и способности учащихся

Выбирают задания, которые будут решать дома.

Записывают домашнее задание.

Формирование навыков самоорганизации