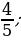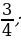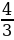| Организационная структура урока |
| Этап урока | Содержание деятельности учителя | Содержание деятельности обучающегося
(осуществляемые действия) | Формируемые способы
деятельности |
| I. Организационный момент | Приветствует обучающихся; проверяет их готовность к уроку. Создает в классе атмосферы психологического комфорта. – Обратите внимание на свои рабочие места. Что вас может отвлекать? | Настраиваются на учебную деятельность. Концентрируют внимание на работе во время урока. Отвечают на вопросы: – Где я? – Зачем я здесь? – Что мне нужно делать? | Формирование навыков самоорганизации |
| II. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | – Какие ассоциации у вас вызывают слова «синус», «косинус», «тангенс», «котангенс»?
Вопрос запуска постановки учебной задачи: – Достаточно ли у вас знаний о понятиях «синус», «косинус», «тангенс», «котангенс»? Формулирует учебную задачу: – Исследовать тригонометрические функции острого угла прямоугольного треугольника | Составляют список слов, которые ассоциируются с понятиями «синус», «косинус», «тангенс», «котангенс». Например: математика, геометрия, угол, треугольник, формула. Анализируют написанные слова. Определяют уровень понимания рассматриваемых понятий. Осознают важность решения поставленной учебной задачи | Развитие навыков целеполагания |
| III. Сообщение темы. Постановка цели и задач урока | Сообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока. – Внимательно прочитайте тему урока. – Что от вас ожидается на уроке? – Какие цели и задачи вы можете перед собой поставить? | Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока: – усвоить суть понятия «синус», «косинус», «тангенс», «котангенс»; – научиться записывать тригонометрические формулы, выражающие связь между тригонометрическими функциями одного и того же угла; – научиться выводить основное тригонометрическое тождество | Умение принимать и сохранять учебную задачу |
| IV. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов: – Почему для меня важно разобраться с тригонометрическими функциями острого угла прямоугольного треугольника? – Где я смогу использовать знания о синусе и косинусе? – Насколько мне интересно узнавать о тригонометрических функциях? – Какова моя цель на данный урок? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Умение выражать свои мысли; развитие навыков самомотивации |
| V. Создание ситуации затруднения. Работа над темой урока.
| Организует осуждение проблемных вопросов: – Как назвать отношение противолежащего катета к гипотенузе в прямоугольном треугольнике? – Как назвать отношение прилежащего катета к гипотенузе в прямоугольном треугольнике?
Организует исследование понятий «синус», «косинус», «тангенс» и «котангенс». Отвечает на вопросы учащихся. Стимулирует самостоятельную исследовательскую деятельность. Помогает найти и проанализировать дополнительную информацию.
Объясняет учащимся, что каждому острому углу α соответствует единственное число – значение синуса (косинуса, тангенса и котангенса) этого угла. Поэтому зависимость значения синуса (косинуса, тангенса и котангенса) острого угла от величины этого угла является функциональной. Функцию, соответствующую этой зависимости, называют тригонометрической. Организует исследование и запоминание формул. Отвечает на вопросы обучающихся.
Вместе с учащимися заполняет таблицу значения синуса, косинуса, тангенса и котангенса для углов 30, 45, 60. Убеждает в важности ее запоминания | Принимают участие в обсуждении проблемных вопросов. Затрудняются ответить на вопросы. Выбирают, как им лучше всего будет организовать свою работу на уроке по изучению нового материала: а) буду самостоятельно изучать новый материал; б) буду работать в паре; в) буду работать в группе. Проводят исследования. Работают с разными источниками информации. Анализируют и систематизируют найденную информацию. | Объект исследования | Найденная информация | Мне непонятно… Вопросы учителю | | Синус | С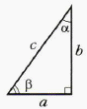 инусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе инусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе 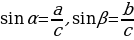
Синус острого угла зависит только от величины этого угла | Как…? | | Косинус | Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе. Обозначение: cos α | Что…? | | Тангенс | Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему. Обозначение: tg α | Почему…? | | Котангенс | Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему. Обозначение: ctg α | Как…? | Делают записи в тетради. Задают вопросы.
Проводят исследование формул. Заполняют таблицу. | Формулы | Мне непонятно… | Вопросы учителю | | 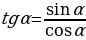
|
|
| | 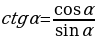
|
|
| | 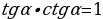
|
|
| | 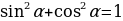
|
|
| | 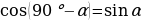
|
|
| | 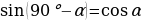
|
|
| | 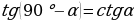
|
|
| | 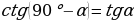
|
|
| Вместе с учителем заполняют таблицу: 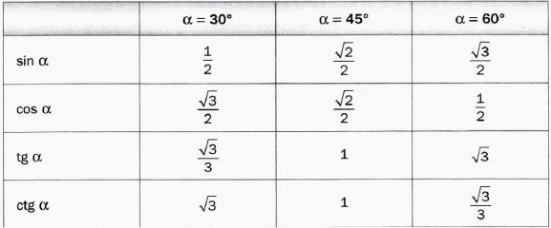
| Умение выражать свои мысли в соответствии с задачей. Умение анализировать информацию
|
| VI. Закрепление изученного материала | Организует самоанализ усвоенных учащимися знаний. Оказывает помощь ученикам, которые не знают ответов на вопросы. Создает условия для дополнительного изучения вопросов, которые вызвали затруднения | Отвечают на вопросы. Определяют свой уровень усвоения знаний. Заполняют таблицу. | Вопросы | Варианты ответов | | Знаю ответ на вопросы (+) | Не знаю ответ на вопрос (+) | | Что называют синусом острого угла прямоугольного треугольника? |
|
| | Что называют косинусом острого угла прямоугольного треугольника? |
|
| | Что называют тангенсом острого угла прямоугольного треугольника? |
|
| | Что называют котангенсом острого угла прямоугольного треугольника? |
|
| | От чего зависит синус, косинус, тангенс и котангенс угла? |
|
| | Как связаны между собой tg α, sin α и cos α? |
|
|
| Умение осуществлять актуализацию полученных знаний и умений |
| VII. Решение заданий | Задание № 581. Катет и гипотенуза прямоугольного треугольника соответственно равны 8 см и 10 см. Найдите: 1) синус угла, противолежащего меньшему катету;
2) косинус угла, прилежащего к большему катету;
3) тангенс угла, противолежащего меньшему катету;
4) котангенс угла, прилежащего к большему катету | Решение.
1) 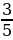 ; ; 2) 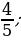 3) 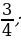 4) 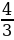 | Умение самостоятельно принимать решения
|
| VIII. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами: – Что нового я узнал на уроке? – Понравилось ли мне изучать тему «Тригонометрические функции острого угла прямоугольного треугольника»? – Получаю ли я удовольствие от умственной работы на уроках геометрии? – Могу ли я лучше учиться? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию. | Умение отслеживать цели учебной деятельности |
| IХ. Домашнее задание | Помогает учащимся выбрать задания из учебника. Обращает внимание на возможности и способности учащихся | Выбирают задания, которые будут решать дома. Записывают домашнее задание. | Формирование навыков самоорганизации |







 инусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе
инусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе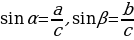
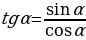
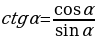
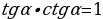
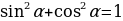
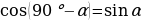
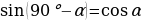
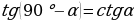
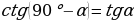

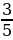 ;
;