Просмотр содержимого документа
«Технологическая карта урока «Введение понятия «Размещение». Решение комбинаторных задач на размещение»»
Технологическая карта урока
Класс: 9 класс
Тема: «Введение понятия «Размещение». Решение комбинаторных задач на размещение»
Цель урока: познакомить учащихся с понятием «Размещение» и отработать учения решать комбинаторные задачи на практике.
Тип урока: изучение нового материала.
Планируемые результаты:
Предметные:
Знать формулу вычисления размещения - 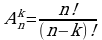
Уметь решать комбинаторные задачи на нахождение числа объектов;
Личностные: представление о математике как сфере человеческой деятельности, находчивость, активность при решении математических задач; способность к эмоциональному восприятию;
Метапредметные: умение видеть математическую задачу в контексте проблемной ситуации в окружающей жизни; умение использовать средства «наглядности» для иллюстрации математической задачи.
УУД, которые актуализируют/приобретут/закрепят обучающиеся в ходе урока/занятия/ мероприятия:
Личностные УУД: мотивация к обучению и целенаправленной познавательной деятельности;
Регулятивные УУД: Целеполагание; планирование;
Коммуникативные УУД: планирование учебного сотрудничества с учителем и сверстниками;
Познавательные УУД: самостоятельное выделение и формулирование познавательной цели.
Краткое описание: в ходе урока учащиеся, путем решения задач из жизни получают знания по теме. Мотивация к изучению урока происходит с помощью активного метода («Работа над понятием»). Начинается урок с беседы, где повторяются кратко знания получение из прошлых уроков в форме беседы, далее плавно перетекает в этап изучения новых знаний, где учащиеся в ходе эксперимента подходят к теме, далее идет усвоение темы за счет решения практических задач.
Ход урока
| Этап проведения урока | Форма организации УД | Инструкция учителя обучающимся |
| 1. Организационный момент. 4 мин.
| - приветствие - вхождение или погружение в тему (целеполагание), - формирование ожиданий обучающихся | Приветствие. Беседа по вопросам: - Какие задачи мы называем комбинаторными? - Может ли комбинаторика помочь в реальной жизни? (обсуждение) Области применения комбинаторики:
-учебные заведения ( составление расписаний) -сфера общественного питания (составление меню) -лингвистика (рассмотрение вариантов комбинаций букв) -география (раскраска карт) -биология (расшифровка кода ДНК) -химия (анализ возможных связей между химическими элементами) -экономика (анализ вариантов купли-продажи акций) -азартные игры (подсчёт частоты выигрышей) -криптография (разработка методов шифрования) -доставка почты (рассмотрение вариантов пересылки) -спортивные соревнования (расчёт количества игр между участниками) |
| 2. Постановка формируемых результатов и задач урока. Мотивация учебной деятельности учащихся. 4 мин. | работа над понятием
| предлагается для зрительного восприятия название темы урока, и учитель просит объяснить значение каждого слова или отыскать в "Толковом словаре".
|
| 3. Актуализация знаний. 4 мин. | интеллектуальная разминка Таблички с понятиями и терминами вывешиваются на доске Интеллектуальная разминка не только настраивает учащихся на учебную деятельность, но и развивает мышление, внимание, умение анализировать, обобщать, выделять главное. | Что такое «перестановки»? - Сколько двузначных чисел можно составить из чисел 1,2,3.4 ,используя в записи числа каждую из них не более одного раза?( 12 чисел). - Даны три буквы А, И, С. Составить всевозможные комбинации из этих букв. (АВС, АСВ, ВАС,ВСА,САВ,СВА -6 комбинаций) - В пятницу у вас 4 уроков: алгебра, русский, физика, история. Сколькими способами можно составить расписание на пятницу? ( 24 способа).
|
| 4. Изучение нового материала. 10 мин.
| - интерактивная лекция, - проработка содержания темы
| Комбинаторика – раздел математики, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую. Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять». Термин "комбинаторика" был введён знаменитым Готфридом Вильгельмом Лейбницем, - всемирно известным немецким учёным. К омбинаторные задачи делятся на несколько групп. омбинаторные задачи делятся на несколько групп. Задача№1. У нас имеется 5 книг, что у нас всего одна полка, и что на ней вмещается лишь 3 книги. Сколькими способами можно расставить на полке 3 книги?
Выбираем одну из 5-ти книг и ставим на первое место на полке. Это мы можем сделать 5-ю способами. Теперь на полке осталось два места и у нас осталось 4 книги. Вторую книгу мы можем выбрать 4-мя способами и поставить рядом с одной из 5-ти возможных первых. Таких пар может быть 5·4. Осталось 3 книги и одно место. Одну книгу из 3-ёх можно выбрать 3-мя способами и поставить рядом с одной из возможных 5·4 пар. Получится 5·4·3 разнообразных троек. Значит всего способов разместить 3 книги из 5-ти 5·4·3 = 60.
Это размещения . Размещением из n элементов по k (k≤n) называется любое множество, состоящее из k элементов, взятых в определённом порядке из данных n элементов. 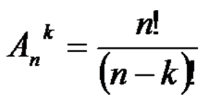
-Какие цели вы для себя поставите сегодня на уроке? Задачи минимум на урок? Научиться решать еще один вид комбинаторных задач Использовать понимание «размещения» в окружающих нас явлениях.
|
| 5. Первичное закрепление нового материала. 15 мин.
| - интерактивная лекция
| Задача №2. Сколькими способами можно составить расписание на день из шести различных уроков, если изучается 14 предметов?
Задача №3. В футбольной команде 11 человек, нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать? Решение. Каждый из 11 человек команды может стать капитаном. С111=11. Каждый из оставшихся 10 членов команды может стать заместителем капитана. С101=10. Поэтому всего способов будет 10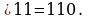 Или 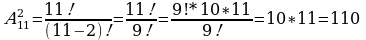 Ответ: 110 способов Задача №4. Из 26 учащихся класса надо выбрать старосту и его заместителя. Сколькими способами это можно сделать? Решение: Из 26 учащихся выбираем 2, причём порядок выбора имеет значение. Количество способов выбора равно 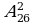 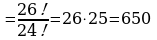 . Ответ: 650 способ . Ответ: 650 способ Задача №5. Сколькими способами могут быть распределены первая, вторая и третья премии между 13 участниками конкурса? Решение: Выбираем трёх призёров из 13 участников конкурса с учётом порядка (кому какая премия): 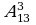 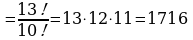 способов. Ответ: 1716 способов способов. Ответ: 1716 способов Задача №6.дополнительная задача. Сколькими способами могут занять первое, второе и третье места 8 участниц финального забега на 100м? Решение Выбор из 8 по 3 с учётом порядка: 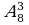 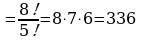 способов. способов. Ответ: 336 способов
|
| 6. Итоги урока. 2 мин.
| - подведение итогов (рефлексия, анализ и оценка урока). | Постановка учащимися себе отметки за урок. -Какие задачи ставили на уроке? - Достигли их? - Кто не справился? -Кому нужна помощь учителя или ученика? -Где можно применять комбинаторные задачи в жизни повседневной?
|
| 7. Информация о домашнем задании. |
| Индивидуальная работа по карточкам. |
Домашнее задание
Задача №1. Сколькими способами 7 книг разных авторов можно расставить на полке в один ряд?
Задача № 2 (о квартете)
В знаменитой басне Крылова “Квартет” “Проказница мартышка, Осел, Козел да косолапый Мишка” исследовали влияние взаимного расположения музыкантов на качество исполнения.
Зададим вопрос: Сколько существует способов, чтобы рассадить четырех музыкантов?
Задача № 3. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? Это пример задачи на размещение без повторений.
Задача № 4. В 5 классе обучается 24 ученика. Сколькими способами можно составить график дежурства по классу, если группа дежурных состоит из трех школьников?
Задача №5. Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?
Задача №6. Четыре друга купили билеты в кино: на 1-е и 2-е места в первом ряду и на 1-е и 2-е места во втором ряду. Сколькими способами друзья могут занять эти 4 места в кинотеатре?
Задача №7. Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов может он выбрать?






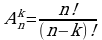
 омбинаторные задачи делятся на несколько групп.
омбинаторные задачи делятся на несколько групп. 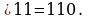
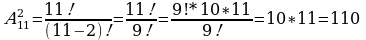
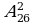
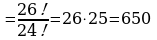 . Ответ: 650 способ
. Ответ: 650 способ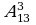
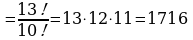 способов. Ответ: 1716 способов
способов. Ответ: 1716 способов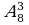
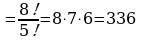 способов.
способов.









