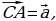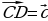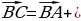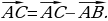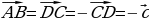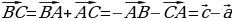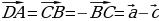Урок «Вычитание векторов» (9 класс, учебник А.Г Мерзляк, В.Б. Полонский, М.С. Якир)
| Организационная структура урока |
| Этап урока | Содержание деятельности учителя | Содержание деятельности обучающегося
(осуществляемые действия) | Формируемые способы
деятельности |
| I. Организационный момент | Приветствует обучающихся; проверяет их готовность к уроку. Создает в классе атмосферу психологического комфорта. – Мне очень нравится, как вы относитесь к урокам геометрии! – Я сегодня постараюсь вам помочь продолжить познавать геометрию! | Настраиваются на учебную деятельность. Концентрируют внимание на работе во время урока.
| Формируют навыки самоорганизации |
| II. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | Предлагает учащимся рассказать о своем «багаже» знаний о векторах: – Что вы уже знаете и умеете?
Вопрос запуска постановки учебной задачи: – Достаточно ли у вас знаний, чтобы выполнить вычитание векторов? Формулирует учебную задачу: – Исследовать вычитание векторов | Выступают перед классом или в группах. – Мы изучали… – Я разобрался с… – Я могу объяснить… – Я выполнял… Осознают важность решения поставленной учебной задачи. | Развивают навыки целеполагания |
| III. Сообщение темы. Постановка цели и задач урока | Сообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока. – Внимательно прочитайте тему урока. – Что от вас ожидается на уроке? – Какие цели и задачи вы можете перед собой поставить? | Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока: – усвоить суть действия вычитания векторов; – научиться выполнять вычитание векторов | Формируют умения принимать и сохранять учебную задачу |
| IV. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов: – Что меня заинтересовало в теме урока? – Почему учиться никогда не поздно? – Каких результатов моей работы на уроке ожидают мои родители? – Какова моя цель на данный урок? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Формируют умения выражать свои мысли. Развивают навыки самомотивации |
| V. Создание ситуации затруднения. Работа над темой урока | Организует обсуждение проблемного вопроса: – Как выполнить вычитание векторов?
Организует изучение понятия «разность векторов».
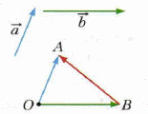
Организует исследование иллюстраций.

Организует анализ теоремы. Помогает сделать вывод: 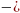 Для любых векторов Для любых векторов 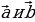 существует единственный вектор существует единственный вектор 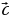 такой, что такой, что 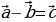 . .
Организует анализ понятия «противоположные векторы». Отвечает на вопросы учащихся.
Объясняет: – Вектор, противоположный вектору 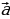 обозначают так: – обозначают так: –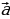 . Вектору . Вектору 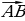 противоположным является вектор противоположным является вектор 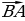 . Для любых точек А и В выполняется равенство . Для любых точек А и В выполняется равенство 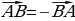
Из правила треугольника следует, что: 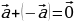
Организует анализ теоремы. Стимулирует самостоятельную познавательную деятельность учащихся | Принимают участие в обсуждении проблемного вопроса. Испытывают определенные трудности при ответе на вопрос. Выбирают, как им лучше всего будет организовать свою работу на уроке по изучению нового материала: А) буду самостоятельно изучать новый материал; Б) буду работать в паре; В) буду работать в группе. Анализируют информацию. Заполняют таблицу: | Информация | Мне непонятно… | Вопросы учителю | | Разностью векторов 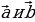 называют такой вектор называют такой вектор 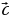 , сумма которого с вектором , сумма которого с вектором 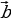 равна вектору равна вектору 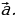 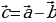
| Каким образом…? Как получили…? | Зачем…? Почему…? | Обсуждают иллюстрации. Осуществляют поиск дополнительной информации. Приходят к выводу, что для любых трех точек О, А и В выполняется равенство 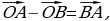 которое выражает правило нахождения разности двух векторов, отложенных от одной точки. которое выражает правило нахождения разности двух векторов, отложенных от одной точки.
Анализируют теорему. Заполняют таблицу. | Теорема | Комментарий ученика к доказательству теоремы | | Если координаты векторов 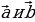 соответственно равны соответственно равны 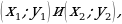 то координаты вектора то координаты вектора 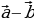 равны равны  ; ; 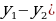
| Каким образом…? | Анализируют определение. Задают вопросы учителю. | Определение | Ключевые слова | Вопросы учителю | | Два ненулевых вектора называют противоположными, если их модули равны и векторы противоположно направлены | Модули равны, векторы противоположно направлены
| Почему…? | Делают записи в тетради. Задают вопросы учителю.
Анализируют теорему. Заполняют таблицу. | Теорема | Я хочу узнать, почему… | | Для любых векторов 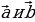 выполняется равенство выполняется равенство 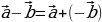
|
|
| Выражают свои мысли в соответствии с задачей.
Анализируют информацию
|
| VI. Закрепление изученного материала | Организует самоанализ усвоенных учащимися знаний. Оказывает помощь ученикам, которые не знают ответов на вопросы. Создает условия для дополнительного изучения вопросов, которые вызвали затруднения
| Отвечают на вопросы. Определяют свой уровень усвоения знаний. Заполняют таблицу. | Вопросы | Варианты ответов | | Знаю ответ на вопрос (+) | Не знаю ответ на вопрос (+) | | Какой вектор называют разностью двух векторов? |
|
| | Какое равенство выражает правило нахождения разности двух векторов, отложенных от одной точки? |
|
| | Чему равны координаты вектора, равного разности двух данных векторов? |
|
| | Какие векторы называют противоположными? |
|
| | Как обозначают вектор, противоположный вектору 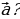 |
|
| Анализируют ответы на вопросы. Проводят дополнительное изучение нового материала. Задают вопросы учителю |
|
| VII. Решение заданий | Задания. 1. (№ 480) Дан треугольник АВС. Выразите вектор 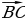 через векторы через векторы 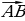 и и 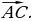
2. (№ 481) Дан параллелограмм ABCD. Выразите векторы 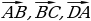 через векторы через векторы 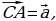 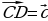 | Решение. 1. 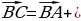 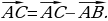 2. 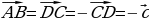 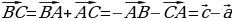 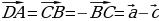 | Развивают умения самостоятельно принимать решения |
| VIII. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами: – Каковы мои достижения на уроке? – С какими трудностями я столкнулся при изучении вычитания векторов? – Что у меня получилось лучше всего? – Какой информацией мне хочется поделиться с друзьями? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию | Отслеживают цель учебной деятельности |
| IX. Домашнее задание | Помогает учащимся выбрать задания из учебника. Обращает внимание на возможности и способности учащихся | Выбирают задания, которые будут решать дома. Записывают домашнее задание. | Формируют навыки самоорганизации |








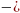 Для любых векторов
Для любых векторов 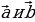 существует единственный вектор
существует единственный вектор 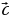 такой, что
такой, что 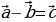 .
.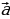 обозначают так: –
обозначают так: –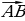 противоположным является вектор
противоположным является вектор 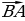 . Для любых точек А и В выполняется равенство
. Для любых точек А и В выполняется равенство 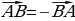
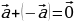
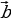 равна вектору
равна вектору 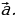
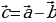
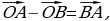 которое выражает правило нахождения разности двух векторов, отложенных от одной точки.
которое выражает правило нахождения разности двух векторов, отложенных от одной точки.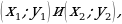 то координаты вектора
то координаты вектора 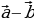 равны
равны 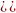 ;
; 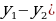
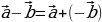
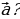
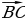 через векторы
через векторы 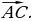
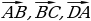 через векторы
через векторы