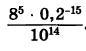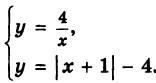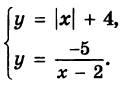Текшеруу иштер 8-класс

Контрольная работа №1 (1 четверть)."Числовые и алгебраические выражения", "Математический язык и математическая модель"

Вариант I 

1. Найдите значение заданного числового выражения:
а) 9,5 - 5,6 + 2,3 - 1,2;
б) 0,4 * ²⁄₇ + 2,3 * ³⁄₇;


2. Решите данные уравнения:
а) 5у + 7 = 4;
б) 8х - 3 = 5 - 2х;


3. Упростите заданное алгебраическое выражение. Вычислите его значение:
12 + 4 *( 3z-4 ) -( 5z+ 6 ), при z=³⁄₄)


4. Решите задачу. При решении используйте этапы математического моделирования.
В библиотеке выдали книги 6, 7 и 8 классам. 6 классу раздали 1,5 раза больше книг чем 7 классу и на 50 книг больше чем 8 классу. Сколько книг выдали каждому классу, если всего выдали 400 книг? 


Вариант II 

1. Найдите значение заданного числового выражения:
а) 8,5 - 1,2 + 2,9 - 4,7;
б) 0,7 * ⁵⁄₇ + 8,4 * ³⁄₇;


2. Решите данные уравнения:
а) 2z - 12 = 4;
б) 7y - 3 = 5 - 3y;


3. Упростите заданное алгебраическое выражение. Вычислите его значение:
54 - 2 * ( 7y + 3 ) -( 3y + 4 ), при y=⁴⁄₇)


4. Решите задачу. При решении используйте этапы математического моделирования.
Портные шили костюмы. Детских костюмов было сшито в 1,5 раза больше чем мужских. А женских костюмов было сшито на 40 штук больше чем мужских. Сколько детских костюмов было сшито, если всего сшили 390 костюмов? 



Вариант III 

1. Найдите значение заданного числового выражения:
а) 12,5 - 8,3 + 5,9 -6,3;
б) 2,3 * ⁴⁄₉ + 1,8 * ⁵⁄₉;


2. Решите уравнения:
а) 4у + 12 = 32;
б) 8х - 12 = 16 - 2х;


3. Упростите заданное алгебраическое выражение. Вычислите его значение:
42 + 4*( 12a - 5) +( 7a - 3), при z=²⁄₅)


4. Решите задачу. При решении используйте этапы математического моделирования.
В три магазина привезли яблоки на продажу. В первый магазин привезли в 2 раза больше, чем во второй. В третий на 70 кг больше, чем в во второй. Сколько кг привезли в каждый магазин, если всего привезли 450 кг яблок? 

Контрольная работа №2 (1 четверть). "Координатная плоскость", "Линейное уравнение с двумя переменными", "Линейная функция"

Вариант I 

1. Задана функция y=3x - 4. Постройте её график.
Используйте его, чтобы найти:
а) На отрезке [-3; 0] рассчитайте максимум и минимум функции;
б) При каких значениях график функции ниже оси ОХ.


2.а) Дано уравнение 4х - 8y +2 = 0. Найдите координаты точек пересечения графика уравнения с осями координат. 
б) Рассчитайте, принадлежит ли данному уравнению точка А (-2; 3¹⁄₂)


3. В какой точке пересекаются прямые: y= 3x; y = x + 2;


4. Вычислите, при каком значении а решением уравнение -aх + 4 y -a =0, является пара чисел (-2; 3).



Вариант II 

1. Задана функция y=4x + 1 Постройте её график.
Используйте его, чтобы найти:
а) На отрезке [0; 12] рассчитайте максимум и минимум функции;
б) При каких значениях график функции выше оси ОХ.


2.а) Дано уравнение 2х + 2y - 5 = 0. Найдите координаты точек пересечения графика уравнения с осями координат. 
б) Рассчитайте, принадлежит ли данному уравнению точка А (-3; 2¹⁄₃)


3. В какой точке пересекаются прямые: y= 2x + 2; y = 3x - 2;


4. Вычислите, при каком значении а решением уравнение aх - 5 y - a =0, является пара чисел (-1; 5).



Вариант III 

1. Задана функция y=2x - 3. Постройте её график.
Используйте его, чтобы найти:
а) На отрезке [-3; 5] рассчитайте максимум и минимум функции;
б) При каких значениях график функции левее оси ОY.


2.а) Дано уравнение х + 3y - 6 = 0. Найдите координаты точек пересечения графика уравнения с осями координат. 
б) Рассчитайте, принадлежит ли данному уравнению точка А (-4; 1¹⁄₂)


3. В какой точке пересекаются прямые: y= 2x + 2; y = 3x - 2;


4. Вычислите, при каком значении а решением уравнение 2aх - 2 y + a =0, является пара чисел (- 3; 4).

Контрольная работа №3 (2 четверть). "Системы двух линейных уравнений (метод постановки и метод сложения)"

Вариант I 

1. Задана система уравнений. Решите систему с помощью графического метода.
 

2. Решите данную систему уравнений методом подстановки.
 

3. Решите следующую систему уравнений методом алгебраического умножения.
 

4. Решите задачу, используя три этапа математического моделирования.
Петя собирает 5 рублёвые и рублёвые монеты. Всего у него 200 монет. Сколько всего у него монет, если всего у него денег на сумму 800 руб.



Вариант II 

1. Задана система уравнений. Решите систему с помощью графического метода.
 

2. Решите данную систему уравнений методом подстановки.
 

3. Решите следующую систему уравнений методом алгебраического умножения.
 

4. Решите задачу, используя три этапа математического моделирования.
Задан прямоугольник. Одна сторона прямоугольника больше другой на 2 см. Если одну сторону прямоугольника увеличить на в 2 раза, а другую на 3 см, то периметр нового прямоугольника будет равен 28 см. Найдите стороны прямоугольника.



Вариант III 

1. Задана система уравнений. Решите систему с помощью графического метода.
 

2. Решите данную систему уравнений методом подстановки.
 

3. Решите следующую систему уравнений методом алгебраического умножения.
 

4. Решите задачу, используя три этапа математического моделирования.
Задан прямоугольник. Длина прямоугольника больше ширины на 2 см. Если увеличить длину стороны на 4 см, то площадь прямоугольника станет равной 48 см². Чему равны стороны прямоугольника?

Контрольная работа №4 (2 четверть). "Степень с натуральным показателем и её свойства"

Вариант I 

1. Упростите заданные выражения:

 

2. Вычислите выражение:
 

3. Решите уравнение:

 

4. Решите задачу, используя три этапа математического моделирования:

Дан квадрат. Его сторону увеличили в 3 раза, и площадь квадрата увеличилась на 128 см². Чему была равна сторона квадрата в самом начале?



Вариант II 

1. Упростите заданные выражения:

 

2. Вычислите выражение:
 

3. Решите уравнение:

 

4. Решите задачу, используя три этапа математического моделирования:

Дан квадрат. Его сторону уменьшили в 3 раза, и площадь квадрата уменьшилась на 116 см². Чему была равна сторона квадрата в самом начале?



Вариант III 

1. Упростите заданные выражения:

 

2. Вычислите выражение:
 

3. Решите уравнение:

 

4. Решите задачу, используя три этапа математического моделирования:

Дан квадрат. Его сторону увеличили на 2 см., и площадь квадрата увеличилась на 28 см². Чему была равна сторона квадрата в самом начале?

Контрольная работа №5 (3 четверть). "Одночлены, операции над одночленами - сложение, вычитание, умножение, возведение в степень"

Вариант I 

1. Задан одночлен. Приведите его к стандартному виду и отметьте его коэффициент:

4,7x³ y² x² y³ z * (- ³⁄₈) x⁴ y³ z

2. Упростите выражение и найдите значение выражения:

5a² - 2a² + a², при х = ⁴⁄₇


3. Упростите выражение:

5c²d - 2c²d + c³d + 2c³d


4. Упростите заданное выражение:

 


Вариант II 

1. Задан одночлен. Приведите его к стандартному виду и отметьте его коэффициент:

5,6у² z³ c² y³ z * (- ⁴⁄₇) y⁵ z² c

2. Упростите выражение и найдите значение выражения:

3t² + 2t² + t², при t = ³⁄₅


3. Упростите выражение:

3d³e - 2d³e + d²c + d²c


4. Упростите заданное выражение:

 


Вариант III 

1. Задан одночлен. Приведите его к стандартному виду и отметьте его коэффициент:

12,3a³ b² a⁴ b² c * (- ³⁄₈) a² b³ c²

2. Упростите выражение и найдите значение выражения:

5k³ + 3k³ + k³, при t = ¹⁄₂


3. Упростите выражение:

8d²e³ - 2d²e³ + d³e + d³e


4. Упростите заданное выражение:

 

Контрольная работа №6 (3 четверть). "Многочлены, действия с многочленами - сложение и вычитание, умножение и деление многочленов.", "Формулы сокращенного умножения"

Вариант I 

1. Выполните умножение:

a) 2y (y+2); б) 3y² x(3+y)

2. Раскройте скобки:

а) (a-3)²; б) (6x² + y²)²

3. Вычислите значение выражения:

(z² + 3z³ - z²) + (z - 1) (z + 1)² при z=3

4. Найдите значение p(x)=p₁(x)+p₂(x), если заданы следующие значения p₁(x)=2z²+3z+2; p₂(x)=z³ - 3z³; 


Вариант II 

1. Выполните умножение:

a) 4z (z - 5); б) 3x² y(4 + y)

2. Раскройте скобки:

а) (2a - 1)²; б) (2x² + 2z²)²

3. Вычислите значение выражения:

(x² + 3x² - 2x²) + (x - 1) (x + 1)² при x=2

4. Найдите значение p(x)=p₁(x)+p₂(x), если заданы следующие значения p₁(x)=3z²+z + 5; p₂(x)=2z³ - 2z³; 


Вариант III 

1. Выполните умножение:

a) 2a (a - 3); б) 4b² b(5 + b)

2. Раскройте скобки:

а) (3x - 2)²; б) (3x² - 4x²)²

3. Вычислите значение выражения:

(x² + 3x² - 2x²) + (x - 1) (x + 1)² при x=2

4. Найдите значение p(x)=p₁(x)+p₂(x), если заданы следующие значения p₁(x)=3y² - y + 3; p₂(x)=2y³ - 3y³; 

Контрольная работа №7 (4 четверть). "Многочлены, формулы сокращенного умножения, разложение многочлена на множители, сокращение алгебраических дробей"

Вариант I 

1. Разложите следующие выражения на множители:

а) 6х³ - 5х²;

б) 15b³ - 3;

б) 4c² + 4c + 4 + 6c;

2. Решите уравнение: 2х³ - 4х² + 2х - 6 = 0;

3. Сократите заданную дробь:^{4 cd3}⁄_2cd;

4. Решите уравнение: 6х² - 2х = 0;

5. Докажите заданное тождество: (x + y)³ + 2xy + x² - y² = x * 2x;



Вариант II 

1. Разложите следующие выражения на множители:

а) 4y³+ 8y²;

б) 2a² - 4;

б) 3z² + 5z + 8 - 4z;

2. Решите уравнение: 4y³ - 2y² + 2y + 8 = 0;

3. Сократите заданную дробь:^2xy2⁄_xyz;

4. Решите уравнение: 5a² - 2a = 0;

5. Докажите заданное тождество: (x - y) ² - 2 xy + 2 x² - y² = x (3x-4y);



Вариант III 

1. Разложите следующие выражения на множители:

а) 3z³ - 6z²;

б) 4c² - 8;

б) 3b² + 6b - 9 +3b;

2. Решите уравнение: 2z³ - 4z² + 3z - 6 = 0;

3. Сократите заданную дробь:^3cd2⁄_cde;

4. Решите уравнение:6b² - 2b = 0;

5. Докажите заданное тождество: 2xy - (x - y) ² - 2 x² = (x - y)(x +y);

Контрольная работа №8 (4 четверть). "Функция y = x² и её график". "Графическое решение уравнений"

Вариант I 

1. Задано значение аргумента. Найдите значение функции y = x².
а) x=-5;

б) х= - ³⁄₄;

2. Постройте график функции:

2.1. y = x² на промежутке [-4;0]

2.2. Постройте график функций y=x², если -1 "

2.3. Постройте график функции y=2+2x, если 1 "

3. Задано уравнение x² = 4x; Решите данное уравнение графическим методом.

4. Задана функция у=f(x), где f(x) = 2x - 6, Найдите f(-2x+3);



Вариант II 

1. Задано значение аргумента. Найдите значение функции y = x².
а) x= 4;

б) х= - ¹⁄₅;

2. Постройте график функции:

2. 1. y = x² на промежутке [-2;3]

2.2. y=x², если - 3 "

2.3. y=4+3x, если 0 "

3. Задано уравнение x² = 5x; Решите данное уравнение графическим методом.

4. Задана функция у=f(x), где f(x) = 3x - 2, Найдите f(- x+1);



Вариант III 

1. Задано значение аргумента. Найдите значение функции y = x².
а) x=-3;

б) х= - ¹⁄₃;

2. Постройте график функции: 

2. 1. y = x² на промежутке [- 3; 1]

2. 2. y=x², если -0 "

2. 3. y = 1+3x, если 3 "

3. Задано уравнение x² = 3x; Решите данное уравнение графическим методом.

4. Задана функция у=f(x), где f(x) = x - 3, Найдите f(-x+3);

Контрольная работа №1. "Основные понятия и свойство алгебраической дроби", "Сложение и вычитание алгебраических дробей с одинаковыми и разными знаменателями"

Вариант I 

1. Найдите значение перемененной х, при котором алгебраическая дробь y + 5 y (y - 5) не имеет смысла?


2. Найдите значение данного выражения: 6 - 3z 36 - z² + 5z 36 - z² при z=-2. 

3. Выполните сложение и вычитание алгебраических дробей:



4. Решите задачу:
Спортсмен проплыл по течению реки 1 км 800 метров за столько же время, сколько 1500 метров по озеру. Какая скорость у спортсмена, если скорость реки 2 км/час. 

5. Задано выражение: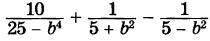
Докажите, что значение данного выражения положительно при всех допустимых значениях переменной. 


Вариант II 

1. Найдите значение перемененной х, при котором алгебраическая дробь y - 7 y (y + 7) не имеет смысла?


2. Найдите значение данного выражения: 6 - 7y² 3-y + 6y² 3 - y при z=-3. 

3. Выполните сложение и вычитание алгебраических дробей:



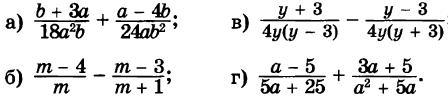
4. Катамаран по течению реки проплывает 24 км за такое же время, что и 20 км против течения. Какова скорость реки, если скорость катамарана 22 км/ч.

5. Задано выражение:

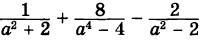
Докажите, что значение данного выражения положительно при всех допустимых значениях переменной. 

Контрольная работа №2. "Умножение и деление алгебраических дробей и возведение их в степень", "Преобразование рациональных выражений", "Степень с отрицательным показателем"

Вариант I 

1. Выполните умножение и деление дробей: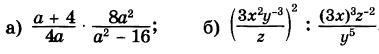

2. Вычислите дробь: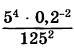

3. Решите уравнение: у + 9y^-1 = 18 

4. Упростите выражение: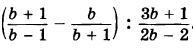

5. Решите задачу:
Из города в село вышел пеший турист. Через 1 час 30 минут вслед за ним вышел велосипедист, скорость которого в 3 раза больше чем у пешехода. Рассчитайте скорость туриста, если в село он пришел в одно время с велосипедистом. Расстояние между городом и селом равно 9 км. 


Вариант II 

1. Выполните умножение и деление дробей: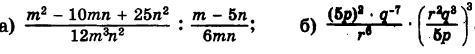

2. Вычислите дробь: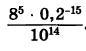

3. Решите уравнение: 36х - х^-1 = 0 

4. Упростите выражение: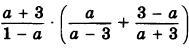
5. Решите задачу.
Из деревни A в деревню B, расстояние между которыми 100 км, выехал грузовик. Через 40 минут вслед за ним мотоцикл. Скорость мотоцикла в 1,5 раза больше чем скорость грузовика. Какая скорость у грузовика, если в деревню В и грузовик и мотоциклист приехали одновременно? 

Контрольная работа №3. "Рациональные и иррациональные числа", "Понятие квадратного корня", "Функция + √х, её свойства и график", "Свойства квадратных корней"

Вариант I 

1. Вычислите:   а) 3,4 √64 - 12;   б) √28 - √63 + √112; 

2. Решите заданное уравнение:   6х² - 7 = 18 - х² 

3. Постройте график функции y = 3 + 2 √x
- Найдите точку пересечения с прямой x - 2y = 0;
- Найдите наименьшее и наибольшее значение функции на отрезке [2; 9].

4. Вычислите:    ( 7 - 4 3 - 2)² 

5. Сократите дробь:   x - 4x + 4 4 - x 

Вариант II 

1. Вычислите:   а) 2,5 √81 + 3;   б) √24 - 4√6 + √54; 

2. Решите заданное уравнение:   2х² + 4 = -14 - х². 

3. Постройте график функции y = -2 √x
- Найдите точку пересечения с прямой 3x - y = 0;
- Найдите наименьшее и наибольшее значение функции на отрезке [1; 7].

4. Вычислите:    ( 14 - 6 5 - 3)² 

5. Сократите дробь:   2b - 2b + 1 b - b 

Контрольная работа №4. "Модуль", "Функция y = kx²", "Функция y = k/x"

Вариант I 

1. Задана функция у = 1,5 х².
a) Постройте график функции;
б) Найдите значение функции, если аргумент равен -3; -1; 4;
в) Найдите значение аргумента, при котором функция будет равна 3;
г) Найдите значение аргумента, при котором функция будет
д) Найдите наибольшее и наименьшее значение функции на отрезке [-4; 0].

2. Решите уравнение графически: 1,5х² = х - 5;

3. Заданы функции: у = f(x) и у = g(x), где f(х) = 4x²; g(x) = x². Найдите значения аргумента, при котором f(x - 3) = g(x +6).

4. Вычислите значение P, при котором уравнение не имеет корней: x² + 1 = p - 3 6 


Вариант II 

1. Задана функция у = 3,5 х².
a) Постройте график функции;
б) Найдите значение функции, если аргумент равен -2; 1; 3;
в) Найдите значение аргумента, при котором функция будет равна 7;
г) Найдите значение аргумента, при котором функция будет
д) Найдите наибольшее и наименьшее значение функции на отрезке [-2; 2].

2. Решите уравнение графически: -1,5х² = х - 3;

3. Заданы функции: у = f(x) и у = g(x), где f(х) = 4/х; g(x) = 1/₂. Найдите значения аргумента, при котором f(x + 1) = g(x² - 1).

4. Вычислите значение P, при котором уравнение не имеет корней: x² + 3 = 3p + 2 4 

Контрольная работа №5. "График функции f(x + l)", "График функции f(x) + m", "График функции f(x + l) + m", "Функция y = ax² + bx + c", "Графическое решение квадратных уравнений"

Вариант I 

1. Задана функция y = √x - 4. Постройте его график и укажите множество значений функции.
2. Задана функция y = x² + 4x + 3. Постройте его график и с помощью графика найдите:
а) промежутки, в которых график возрастает;
б) промежутки в которых график убывает;
в) наибольшее значение функции;
г) при каких значениях x y
3. Решите графически заданное уравнение y = x² - 2x - 8.
4. Задана прямая х=-1. Известно, что она является осью симметрии для параболы y=px² - (p + 12)x - 15.
5. Решите графически систему уравнений: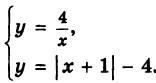


Вариант II 

1. Задана функция y = √x + 5. Постройте его график и укажите множество значений функции.
2. Задана функция y = -x² + 2x + 3. Постройте его график и с помощью графика найдите:
а) промежутки, в которых график возрастает;
б) промежутки в которых график убывает;
в) наибольшее значение функции;
г) при каких значениях x y
3. Решите графически заданное уравнение y = -x² - 3x + 4 =0.
4. Задана прямая х=-1. Известно, что она является осью симметрии для параболы y=px² - (p + 12)x - 15.
5. Решите графически систему уравнений: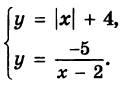

Контрольная работа №6. "Формулы корней квадратных уравнений", "Рациональные уравнения"

Вариант I 

1. Определите количество корней у заданных уравнений:
а)2x² + х + 5 = 0;      б)x² -11x - 42 = 0.

2. Решите заданные уравнения:
а)x² + 7х - 60 = 0;      б)-x² -3x - 6 = 0.
3. Решите уравнение: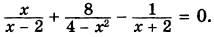
4. Катет прямоугольного треугольника на 6 см меньше другого каткта. Чему равны катеты треугольника, если площадь треугольника равна 56 см².
5. Вычислите значение p уравнения, если уравнение x² p x + 2 = 0 имеет только один корень?


Вариант II 

1. Определите количество корней у заданных уравнений:
а)-x² + 3х - 7 = 0;      б)0,5x² -x - 8 = 0.

2. Решите заданные уравнения:
а)-2x² -5х - 2 = 0;      б)-3x² - 10x - 3 = 0.

3. Решите уравнение: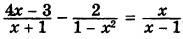
4. У прямоугольника одна сторона меньше другой на 4 см. Найдите стороны прямоугольника, если его диагональ равна 18 см.
5. Вычислите значение p уравнения, если уравнение (p + 2)x² (p + 2)x + 2 = 0 имеет только один корень?

Контрольная работа №7. "Рациональные уравнения как математическая модель", "Частные случаи корней квадратного уравнения","Теорема Виета"

Вариант I 

1. Решите уравнения:
а)2x² + х + 5 = 0;      б)x² - 11x - 42 = 0.

2. Сократите дробь: x 2 - 64 x 2 - 11 x + 24 

3. Отношение у корней данного квадратного уравнения x² + 2x + m равно 6. Найдите корни уравнения и значение m. 

4. Решите задачу:
Автобус проехал 60 км по асфальтированной дороге и 32 км по грунтовой дороге. На всю дорогу он затратил 60 минут. Найдите скорость автобуса на каждом участке, если на шоссе он двигался ан 20 км/ч быстрее. 

5. Упростите выражение: ( x x + 2 + 4 x 2 - 3х - 2 x - 5 ) : x - 7 x 2 + 2x 

Вариант II 

1. Решите уравнения:
а)7x² + 4х + 5 = 0;      б)x² - 106x + 693 = 0.

2. Сократите дробь: 3x 2 - 25x - 18 x 2 - 5 x - 36 

3. Вычислите значение параметра q, при котором один из корней уравнения x² + qx + 48 = 0 в 3 раза больше другого . 

4. Решите задачу:
Расстояние между двумя городами А и Б равно 240 км. Навстречу друг другу одновременно выехали 2 автомашины "Газ" и "Урал". Скорость автомобиля "Газ"больше скорости автомобиля "Урал" на 20 км/час. Поэтому "Газ" проехал свой путь от А до Б на 1 час быстрее, чем "Урал" от пункта Б до А. Найдите скорости автомобилей. 

5. Упростите выражение: x 2 - 9 10 + 3x * ( 2 x - 4 - 4х x 2 - x - 12 - 1 x + 3 ) 

Контрольная работа №8. "Свойства числовых неравенств", "Монотонность функций", "Линейные и квадратные неравенства"

Вариант I 

1. Решите неравенства:
а)x² + 7х - 8 0;      б)3x² - 4x - 1

2. Решите уравнения: а) 5х - 18 2,5 √х - 8 =0; б) √33 - 8 х = х; 

3. При каких значениях параметра m уравнение x²- 2 (m + 3)x + 16 имеет хотя бы один корень? 

4. Найдите область определения для выражения √2 - 5х 

Вариант II 

1. Решите неравенства:
а)12x + 8 ² - 11x - 24

2. Решите уравнения: а) 3x - 2√х - 8 =0; б) √2х + 15 = х; 

3. При каких значениях параметра m уравнение mx²- 2mx + 9 имеет два корня? 

4. Найдите область определения для выражения 1 / _{√4x +3}