Просмотр содержимого документа
«Текст математической олимпиады техникума среди обучающихся 1 курса 2013-2014 учебный год»
Текст математической олимпиады техникума
среди обучающихся 1 курса
2013-2014 учебный год
Задача 1.
(3 балла)
Найдите значение выражения
 при
при  .
.
Решение.
Применяя формулу ( х – у )( х + у ) = х² – у² последовательно для последних двух множителей, в результате получим:
(1- )(1+
)(1+ ) = 1 - a.
) = 1 - a.
При а = 2003 получим 1– а = 1 – 2003 = – 2002.
Ответ: – 2002.
Задача 2.
(3 балла)
Сколько цифр содержит число 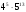 ?
?
Решение.
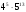 =(
=( )
) =
= =1 250 000 000 000.
=1 250 000 000 000.
Задача 3.
(4 балла)
Маша, Люда, Женя и Катя умеют играть на различных инструментах (виолончели, рояле, гитаре и скрипке), но только на одном. Они же владеют различными иностранными языками ( английским, французским, немецким и испанским ), но каждая только одним. Известно, что девушка, которая играет на гитаре, говорит по-испански; Люда не играет ни на скрипке, ни на виолончели и не знает английского языка; Маша не играет ни на скрипке, ни на виолончели и не знает английского языка; Женя знает французский язык, но не играет на скрипке. Кто на каком инструменте играет и какой иностранный язык знает?
Решение.
Задача имеет 2 варианта решения :
1) Люда играет на гитаре и знает испанский язык;
Маша играет на рояле и знает немецкий язык;
Женя играет на виолончели и знает французский язык;
Катя играет на скрипке и знает английский язык.
2) Маша играет на гитаре и знает испанский язык;
Люда играет на рояле и знает немецкий язык;
Женя играет на виолончели и знает французский язык;
Катя играет на скрипке и знает английский язык.
Задача 4.
(4 балла)
Решите уравнение 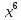 -14
-14 +56
+56 -64=0
-64=0
Решение : 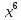 -14
-14 +56
+56 -64 = 0.
-64 = 0.
Пусть  = t, t≥0. Тогда уравнение примет вид :
= t, t≥0. Тогда уравнение примет вид :
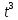 - 14
- 14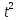 + 56 t- 64 = 0,
+ 56 t- 64 = 0,
(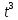 - 64)+( - 14
- 64)+( - 14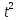 + 56 t) = 0,
+ 56 t) = 0,
(t-4)( 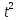 +4 t+16) - 14t (t-4) = 0,
+4 t+16) - 14t (t-4) = 0,
(t-4)(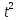 +4 t+16- 14t) = 0,
+4 t+16- 14t) = 0,
(t-4)( t+16) = 0,
t+16) = 0,
t = 4 или  t+16 = 0,
t+16 = 0,
t = 8 или t = 2.
Итак, х = 2, х = -2, х = 2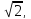 х = - 2
х = - 2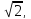 х =
х = 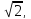 х = -
х = -  .
.
Ответ : - 2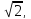 -2, -
-2, - 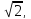
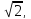 2, 2
2, 2
Задача 5.
(6 баллов)
Доказать, что квадрат высоты равнобедренной трапеции, в которую можно вписать окружность, равен произведению ее оснований.
Решение.
Так как в четырехугольнике, описанном около окружности, суммы длин противоположных сторон равны, то








 при
при  .
. )(1+
)(1+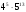 ?
? )
) =
= =1 250 000 000 000.
=1 250 000 000 000.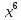 -14
-14 +56
+56 -64=0
-64=0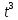 - 14
- 14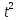 + 56 t- 64 = 0,
+ 56 t- 64 = 0, t+16) = 0,
t+16) = 0,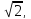 х = - 2
х = - 2









