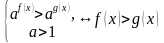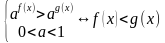Показательные уравнения.
Решение показательных уравнений.
Решение систем показательных уравнений
-
Уравнение - это равенство, содержащее неизвестную величину, значение которой нужно найти.
-
Корень уравнения – это значение неизвестной величины, при котором равенство не теряет смысла.
-
Решить уравнение – значит найти все его корни или доказать, что корней нет.
-
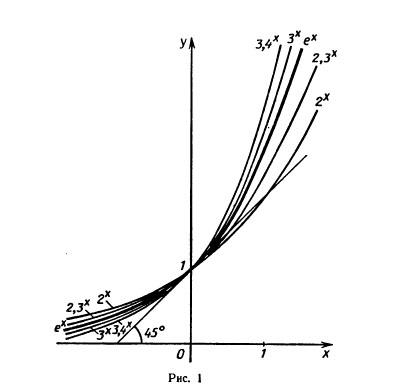
Функция, заданная формулой у = ах (где а 0, а≠ 1), называется показательной функцией с основанием а.
D (y) = R (область определения – множество всех действительных чисел).
E (y) = R+ (область значений – все положительные числа).
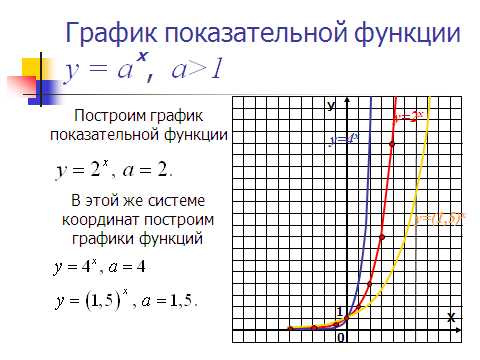
При а 1, функция возрастает. При 0
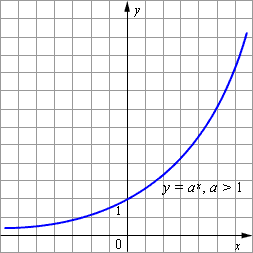
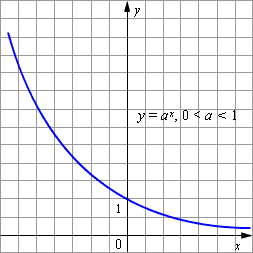
Показательные уравнения
Показательными уравнениями называются уравнения, содержащие переменную в показателе степени.
Самое простое показательное уравнение имеет вид 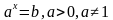
При решении показательных уравнений полезно будет следствие из теоремы о свойствах показательной функции:
Пусть 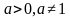 . Если степени с основанием
. Если степени с основанием 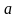 равны, то их показатели равны, т.е. если
равны, то их показатели равны, т.е. если 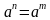 , то
, то  .
.
Примеры показательных уравнений:
5х+2 = 125
3х·2х = 8х+3
32х+4·3х-5 = 0
Обратите внимание! В основаниях степеней (внизу) - только числа. В показателях степеней (вверху) - самые разнообразные выражения с иксом. Если, вдруг, в уравнении вылезет икс где-нибудь, кроме показателя, например: 2х = 3+х - это будет уже уравнение смешанного типа. Такие уравнения не имеют чётких правил решения. Мы их пока рассматривать не будем. Здесь мы будем разбираться с решением показательных уравнений в чистом виде.
Вообще-то, даже чистые показательные уравнения чётко решаются далеко не всегда. Но существуют определённые типы показательных уравнений, которые решать можно и нужно. Вот эти типы мы и рассмотрим.
Решение простейших показательных уравнений
Основными методами решения показательных уравнений являются:
Для начала решим что-нибудь совсем элементарное. Например:
3х = 32
Даже безо всяких теорий, по простому подбору ясно, что х=2. Больше-то никак, верно!? Никакое другое значение икса не катит. А теперь глянем на запись решения этого хитрого показательного уравнения:
3х = 32
х = 2
Что мы сделали? Мы, фактически, просто выкинули одинаковые основания (тройки). Совсем выкинули. И, что радует, попали в точку!
Действительно, если в показательном уравнении слева и справа стоят одинаковые числа в каких угодно степенях, эти числа можно убрать и приравнять показатели степеней. Математика позволяет. Остаётся дорешать куда более простое уравнение.
Однако, запомним железно: убирать основания можно только тогда, когда слева и справа числа-основания находятся в гордом одиночестве! Безо всяких соседей и коэффициентов.
Скажем, в уравнениях: 2х+2х+1 = 23, или 2·2х = 24 двойки убирать нельзя!
Ну вот, самое главное мы и освоили. Как переходить от показательных выражений к более простым уравнениям.
Теперь вы знаете, куда надо стремиться при решении замороченных примеров. Надо приводить его к виду, когда слева - справа стоит одно и то же число-основание. Дальше всё будет легче. Собственно, это и есть классика математики. Берём исходный пример и преобразовываем его к нужному нам виду. По правилам математики, разумеется.
Рассмотрим примеры, которые требуют некоторых дополнительных усилий для приведения их к простейшим. Назовём их простыми показательными уравнениями.
Решение простых показательных уравнений. Примеры
При решении показательных уравнений, главные правила - действия со степенями. Без знаний этих действий ничего не получится.
К действиям со степенями надо добавить личную наблюдательность и смекалку. Нам требуются одинаковые числа-основания? Вот и ищем их в примере в явном или зашифрованном виде.
Посмотрим, как это делается на практике?
Пусть нам дан пример:
22х - 8х+1 = 0
Первый взгляд - на основания. Они разные! Два и восемь. Но впадать в уныние - рано. Самое время вспомнить, что
8 = 23
Вполне можно записать 8х+1 = (23)х+1
Если вспомнить формулу из действий со степенями: (аn)m = anm, то вообще отлично получается:
8х+1 = (23)х+1 = 23(х+1)
Исходный пример стал выглядеть вот так 22х - 23(х+1) = 0
Переносим 23(х+1) вправо (элементарных действий математики никто не отменял!), получаем:
22х = 23(х+1)
Вот, практически, и всё. Убираем основания:
2х = 3(х+1)
Решаем этого монстра и получаем
х = -3
Это правильный ответ.
В этом примере нас выручило знание степеней двойки. Мы опознали в восьмёрке зашифрованную двойку. Этот приём (шифровка общих оснований под разными числами) - очень популярный приём в показательных уравнениях! Надо уметь узнавать в числах степени других чисел. Это крайне важно для решения показательных уравнений.
Дело в том, что возвести любое число в любую степень - не проблема. Перемножить, хоть на бумажке, да и всё. Например, возвести 3 в пятую степень сможет каждый. 243 получится, если таблицу умножения знаете.) Но в показательных уравнениях гораздо чаще надо не возводить в степень, а наоборот... Узнавать, какое число в какой степени скрывается за числом 243, или, скажем, 343... Здесь вам никакой калькулятор не поможет.
Степени некоторых чисел надо знать в лицо, да... Потренируемся?
Определить, какими степенями и каких чисел являются числа:
2; 8; 16; 27; 32; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729, 1024.
Предположим, что вы приняли к сведению информацию о знакомстве с числами. Напомню ещё, что для решения показательных уравнений применим весь запас математических знаний.
Например, при решении показательных уравнений очень часто помогает вынесение общего множителя за скобки. Смотрим пример:
32х+4 -11·9х = 210
И вновь, первый взгляд - на основания! Основания у степеней разные... Тройка и девятка. А нам хочется, чтобы были - одинаковые. Что ж, в этом случае желание вполне исполнимое! Потому, что:
9х = (32)х = 32х
По тем же правилам действий со степенями:
32х+4 = 32х·34
Вот и отлично, можно записать:
32х·34 - 11·32х = 210
Мы привели пример к одинаковым основаниям. И что дальше!? Тройки-то нельзя выкидывать... Тупик?
Вовсе нет. Запоминаем самое универсальное и мощное правило решения всех математических заданий:
Не знаешь, что нужно - делай, что можно!
Что в этом показательном уравнении можно сделать? Да в левой части прямо просится вынесение за скобки! Общий множитель 32х явно намекает на это. Попробуем, а дальше видно будет:
32х(34 - 11) = 210
Что ещё можно сделать? Посчитать выражение в скобках:
34 - 11 = 81 - 11 = 70
Пример становится всё лучше и лучше!
70·32х = 210
Вспоминаем, что для ликвидации оснований нам необходима чистая степень, безо всяких коэффициентов. Нам число 70 мешает. Вот и делим обе части уравнения на 70, получаем:
32х = 3
32х = 31
2х = 1
х = 0,5
Это окончательный ответ.
Случается, однако, что выруливание на одинаковые основания получается, а вот их ликвидация - никак. Такое бывает в показательных уравнениях другого типа. Освоим этот тип.
Замена переменной в решении показательных уравнений.
Пример. Решим уравнение:
4х - 3·2х +2 = 0
Сначала - как обычно. Переходим к одному основанию. К двойке.
4х = (22)х = 22х
Получаем уравнение:
22х - 3·2х +2 = 0
А вот тут и зависнем. Предыдущие приёмы не сработают, как ни крутись. Придётся доставать из арсенала ещё один могучий и универсальный способ. Называется он замена переменной.
Суть способа проста до удивления. Вместо одного сложного значка (в нашем случае - 2х) пишем другой, попроще (например - t). Такая, казалось бы, бессмысленная замена приводит к потрясным результатам!) Просто всё становится ясным и понятным!
Итак, пусть
2х = t
Тогда 22х = 2х2 = (2х)2 = t2
Заменяем в нашем уравнении все степени с иксами на t:
t2 - 3t+2 = 0
Решаем через дискриминант, получаем:
t1 = 2
t2 = 1
Тут, главное, не останавливаться, как бывает... Это ещё не ответ, нам икс нужен, а не t. Возвращаемся к иксам, т.е. делаем обратную замену. Сначала для t1:
t1 = 2 = 2х
Стало быть,
2х = 2
х1 = 1
Один корень нашли. Ищем второй, из t2:
t2 = 1 = 2х
2х = 1
Слева 2х, справа 1. Достаточно вспомнить (из действий со степенями, да...), что единица - это любое число в нулевой степени. Любое. Какое надо, такое и поставим. Нам нужна двойка. Значит:
1 = 20
2х = 20
х2 = 0
Вот теперь всё. Получили 2 корня:
х1 = 1
х2 = 0
Это ответ.
При решении показательных уравнений в конце иногда получается какое-то неудобное выражение. Типа:
2х = 7
Из семёрки двойка через простую степень не получается. Не родственники они... Как тут быть? Для этого введено понятие логарифма и
x = log27
Практические советы
1. Первым делом смотрим на основания степеней. Смотрим, нельзя ли их сделать одинаковыми. Пробуем это сделать, активно используя действия со степенями. Не забываем, что числа без иксов тоже можно превращать в степени!
2. Пробуем привести показательное уравнение к виду, когда слева и справа стоят одинаковые числа в каких угодно степенях. Используем действия со степенями и разложение на множители. То что можно посчитать в числах - считаем.
3. Если второй совет не сработал, пробуем применить замену переменной. В итоге может получиться уравнение, которое легко решается. Чаще всего - квадратное. Или дробное, которое тоже сводится к квадратному.
4. Для успешного решения показательных уравнений надо степени некоторых чисел знать "в лицо".
Решение систем показательных уравнений
Решить системы уравнений:
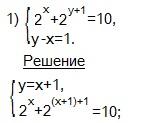
Выразим у через х из (2) -го уравнения системы и подставим это значение в (1) -ое уравнение системы.
Решаем (2) -ое уравнение полученной системы:
2х+2x+2=10, применяем формулу: ax+y=ax∙ay.
2x+2x∙22=10, вынесем общий множитель 2х за скобки:
2х(1+22)=10 или 2х∙5=10, отсюда 2х=2.
2х=21, отсюда х=1. Возвращаемся к системе уравнений.
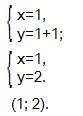
Ответ: (1; 2).
Индивидуальная работа № 1
| Вариант 1 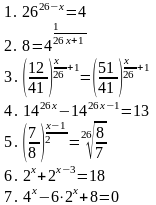
| Вариант 2 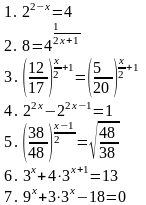
| Вариант 3 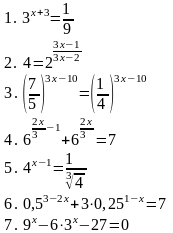
| Вариант 4 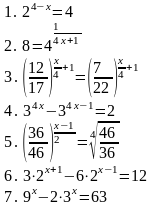
|
| Вариант 5 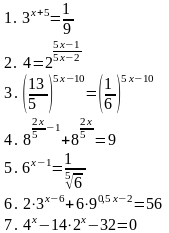
| Вариант 6 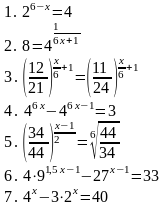
| Вариант 7 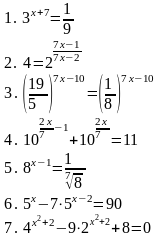
| Вариант 8 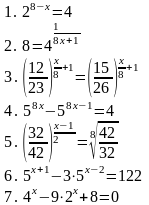
|







 , где m - целое число, а n - натуральное число, называют рациональным числом.
, где m - целое число, а n - натуральное число, называют рациональным числом.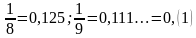
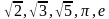
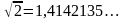
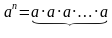 ,
, 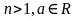
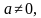 то
то 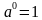
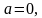 то
то  – не определяется.
– не определяется.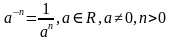
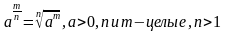
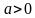 . Степенью числа а с иррациональным показателем
. Степенью числа а с иррациональным показателем 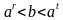 при любых рациональных значениях
при любых рациональных значениях 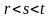 . Это число
. Это число 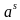 .
.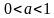 . Степенью числа а с иррациональным показателем
. Степенью числа а с иррациональным показателем 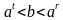 при любых рациональных значениях
при любых рациональных значениях 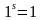 .
.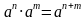
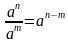
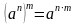
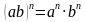
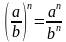
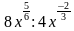 ;
; 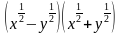
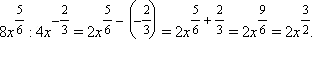
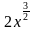 ; 2) x – y.
; 2) x – y.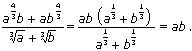
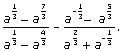
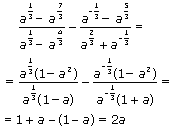
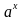 , где а – постоянная,
, где а – постоянная, 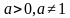 , а
, а 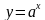 , где а – постоянная,
, где а – постоянная, 
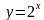 .
. 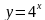 и
и 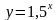
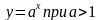 имеет вид
имеет вид
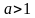
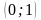 и не пересекается с осью абсцисс.
и не пересекается с осью абсцисс.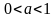
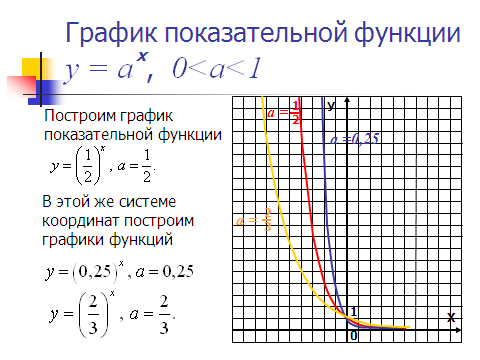
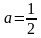 , т.е.
, т.е. 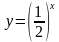 .
.  и
и 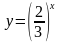
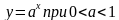 имеет вид
имеет вид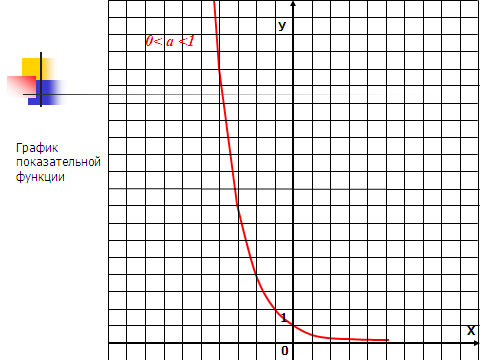
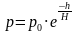 , где
, где 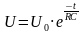 , где
, где 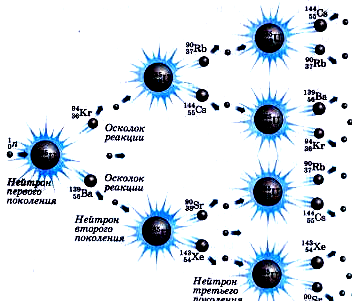 апример, за время равное
апример, за время равное 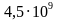 лет при распаде урана -238 распадается половина от начального числа атомов, т.е. при увеличении времени на 4,5 миллиарда лет число атомов уменьшается в 2 раза.
лет при распаде урана -238 распадается половина от начального числа атомов, т.е. при увеличении времени на 4,5 миллиарда лет число атомов уменьшается в 2 раза. Задание. Сделать аналитическую запись формулы радиоактивного распада, обозначив начальную массу вещества М. Изобразить схематически график функции.
Задание. Сделать аналитическую запись формулы радиоактивного распада, обозначив начальную массу вещества М. Изобразить схематически график функции.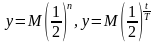

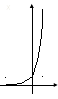
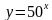
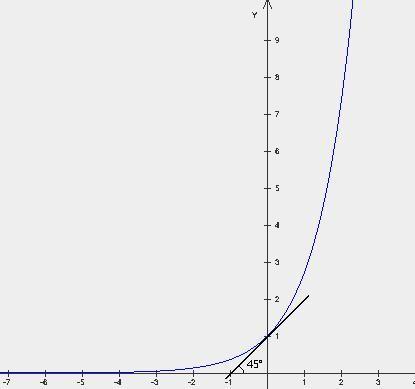 исло
исло 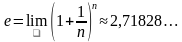 появилось сравнительно недавно.
появилось сравнительно недавно. 

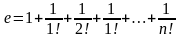

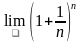 . Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690-1691 годы.
. Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690-1691 годы.
 укву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа "Механика, или Наука о движении, изложенная аналитически" 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.
укву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа "Механика, или Наука о движении, изложенная аналитически" 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.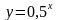 и
и 

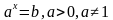
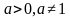 . Если степени с основанием
. Если степени с основанием 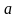 равны, то их показатели равны, т.е. если
равны, то их показатели равны, т.е. если 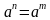 , то
, то  .
.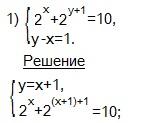
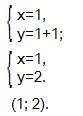
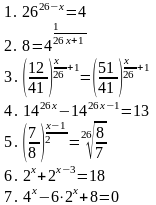
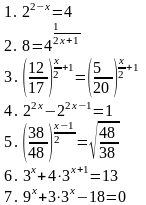
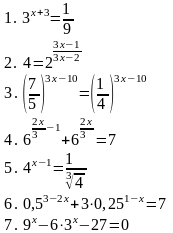
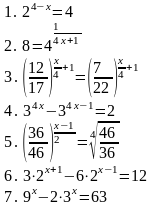
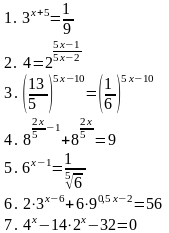
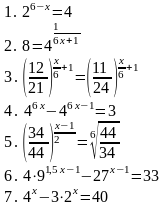
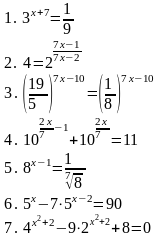
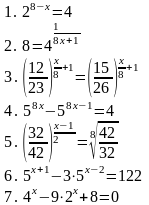
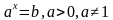
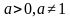 . Если степени с основанием
. Если степени с основанием  равны, то их показатели равны, т.е. если
равны, то их показатели равны, т.е. если 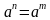 , то
, то 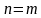 .
.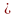 R)
R) 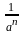 (а
(а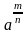 =
= 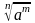 (
(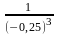
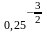 =
= 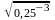 =
= 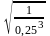 =
=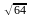 = 8
= 8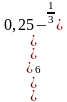 =(0,25)-2 = 42 = 16
=(0,25)-2 = 42 = 16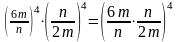 =34=81
=34=81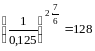 ;
; 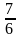 ;
;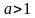 . Если
. Если  , то
, то 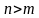 .
.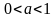 . Если
. Если 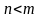 .
.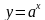 :
: