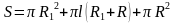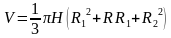Сфера и шар.
Сечение сферы и шара плоскостью.
Касательная плоскость к сфере
Шар или сфера?




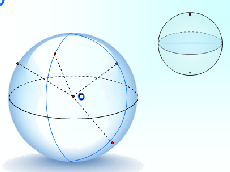
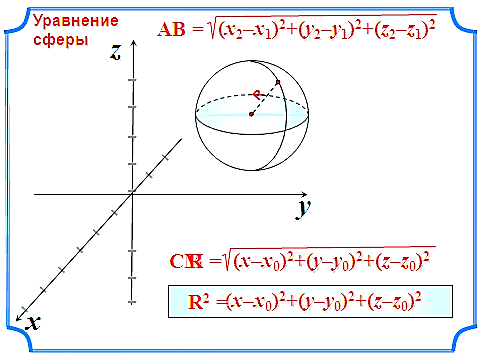
Сфера
Сферой называется геометрическая фигура, состоящая из всех точек пространства, находящихся на заданном расстоянии от данной точки пространства.
Даная точка называется центром сферы.
Радиусом сферы называется отрезок, соединяющий центр сферы с какой-либо точкой сферы.
Хордой сферы называется отрезок, соединяющий две точки сферы.
Диаметром сферы называется хорда, проходящая через ее центр.
Шар
Шаром называется геометрическое тело, состоящее из сферы и части пространства, ограниченного этой сферой.
Радиусом, хордой и диаметром шара называется радиус, хорда и диаметр сферы, которая является границей шара.

Взаимное расположение сферы и плоскости
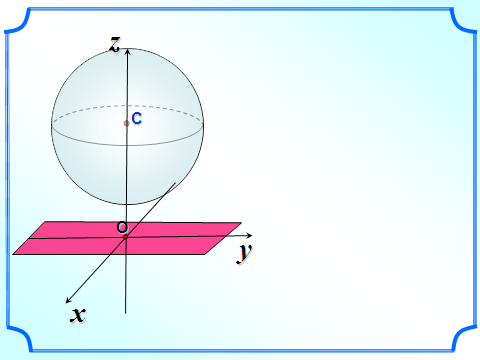
-
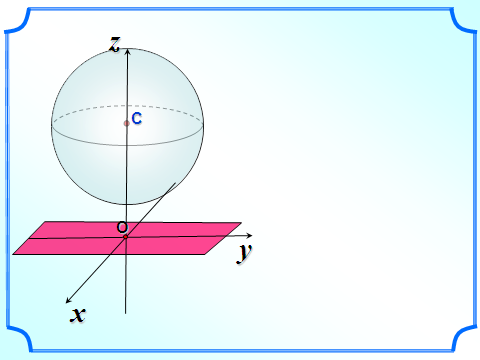
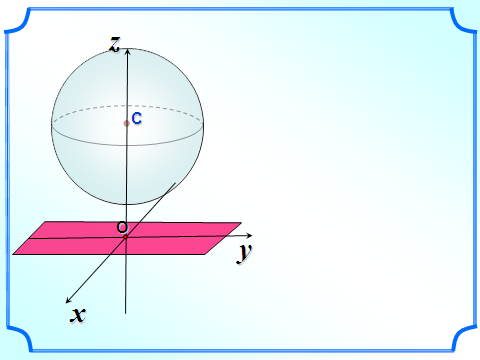
Сфера и плоскость не имеют общих точек
-
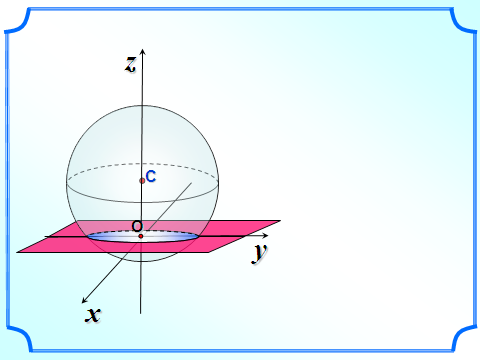
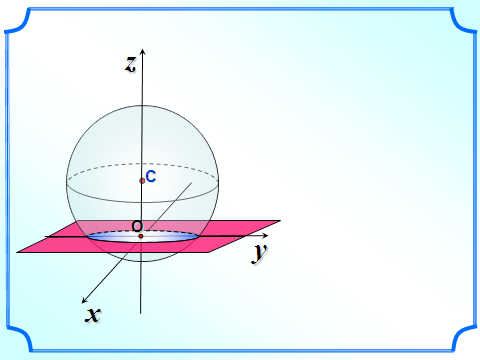
Сфера и плоскость имеют множество общих точек
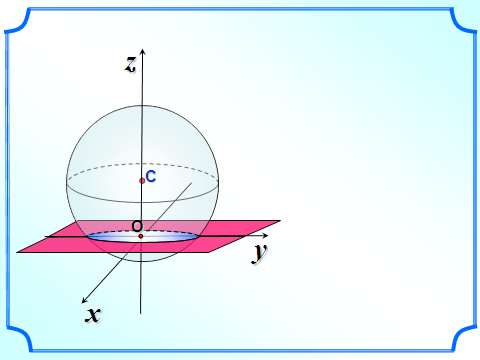
В этом случае плоскость называется секущей плоскостью сферы (шара).
Сечение сферы плоскостью есть окружность.
Сечение шара плоскостью есть круг, а основание перпендикуляра, проведенного из центра шара к плоскости сечения, есть центр круга, полученного в сечении.
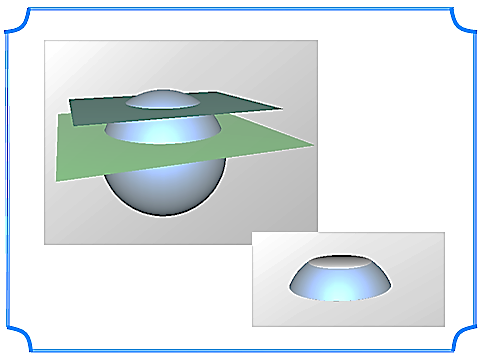
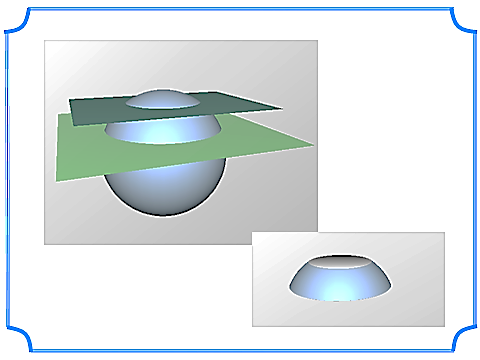
Плоскость, проходящая через центр сферы (шара) называется диаметральной плоскостью.
Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).
Сечения сферы
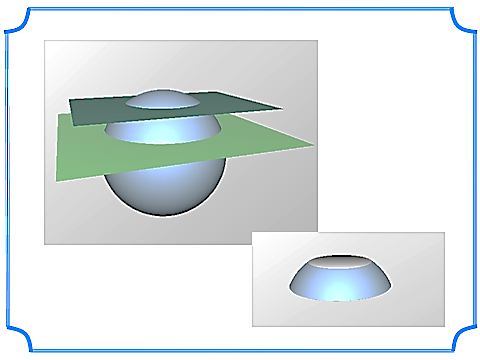
-
С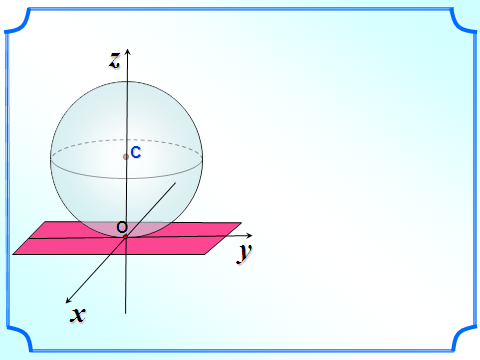 фера и плоскость имеют одну общую точку
фера и плоскость имеют одну общую точку
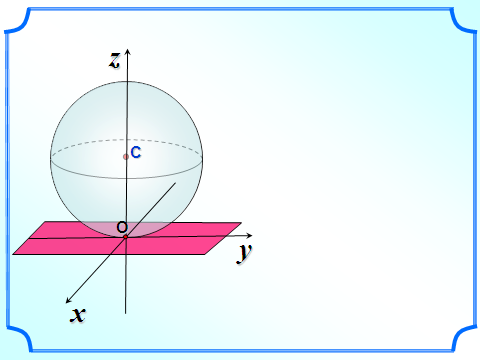
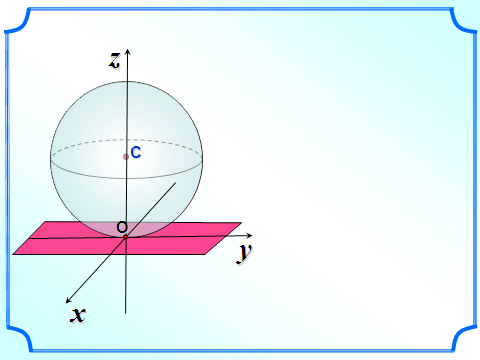
Если плоскость и сфера имеют одну обую точку, то такая плоскость называется касательной плоскостью к сфере (шару).
Касательная плоскость к сфере
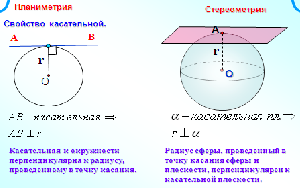
Касательная плоскость к сфере (шару)
Касательной плоскостью к сфере называется плоскость, имеющая со сферой только одну общую точку, а их общая точка называется точкой касания плоскости и сферы.
Касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара.
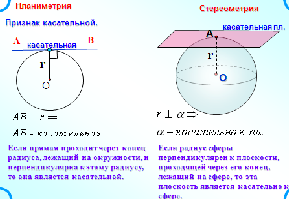
Прямая, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной к сфере (шару).
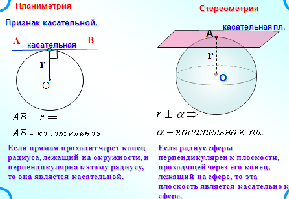
Признак касательной плоскости к сфере
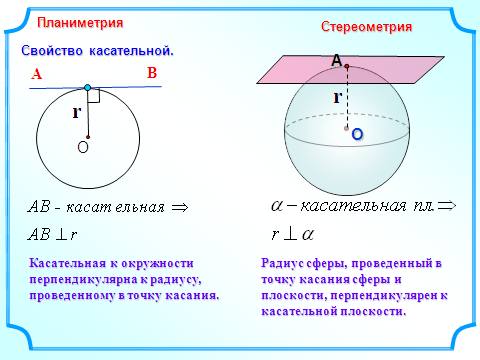
Плоскость, перпендикулярная радиусу сферы и проходящая через его конец, лежащий на сфере, касается сферы.
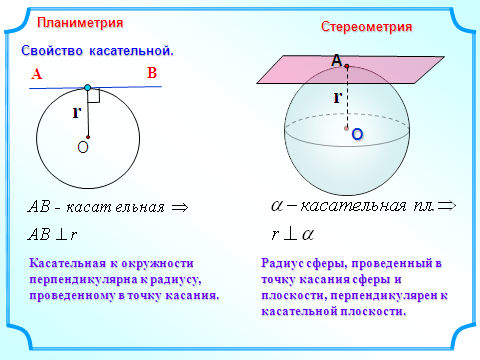
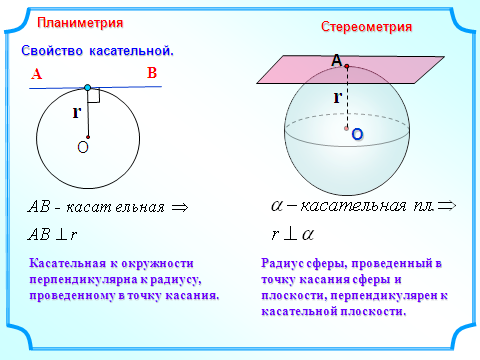
Свойство касательной плоскости к сфере
Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точке касания.
Решение задач
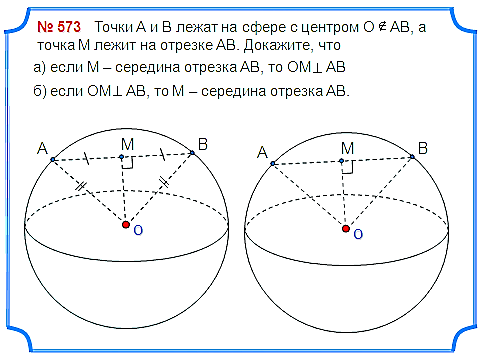
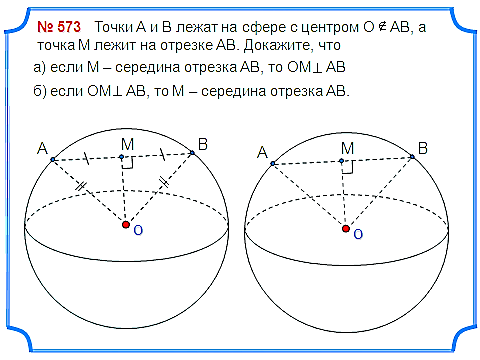
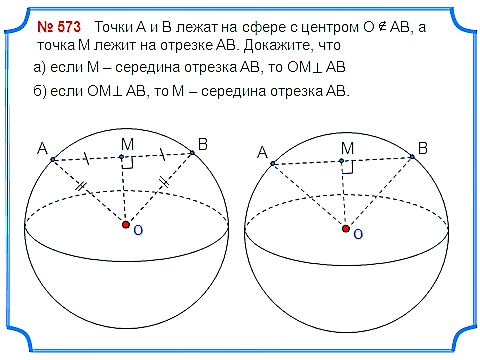
Задача 1. Точки А и В лежат на сфере с центром О АВ, а точка М лежит на отрезке АВ. Докажите, что а) если М – середина отрезка АВ, то OM перпендикулярно AB; б) если OM перпендикулярно AB, то М – середина отрезка АВ.
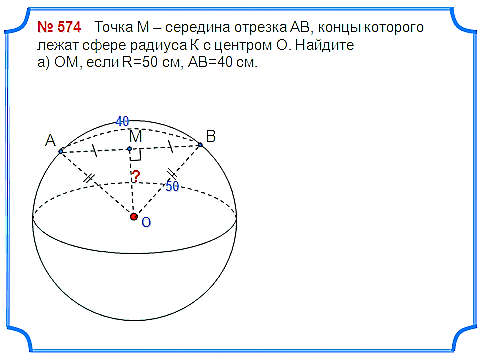
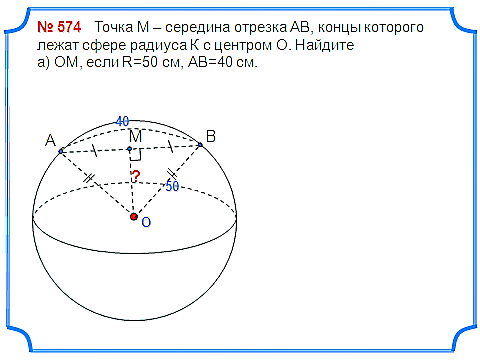
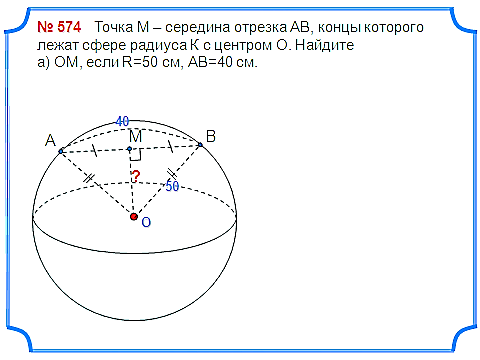
Задача 2. Точка М – середина отрезка АВ, концы которого лежат сфере радиуса К с центром О. Найдите а) ОМ, если R=50 см, АВ=40 см.
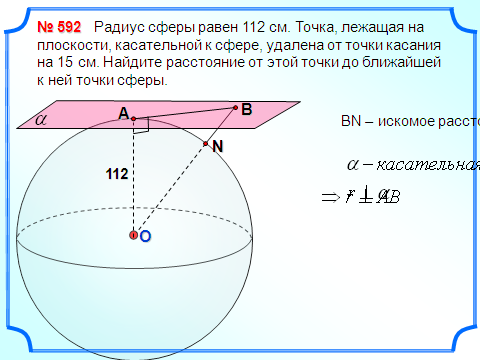
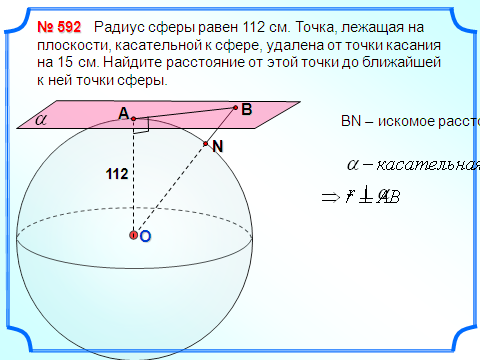
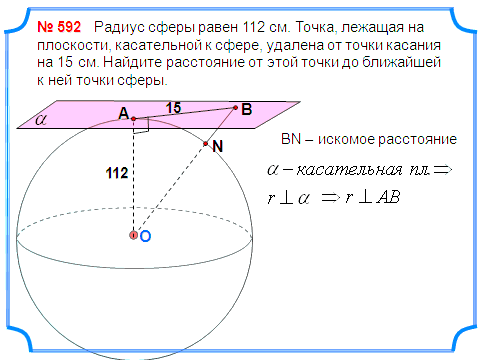
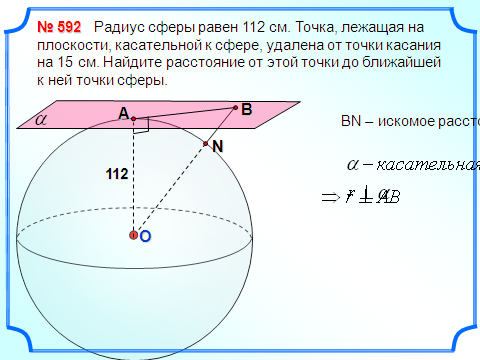
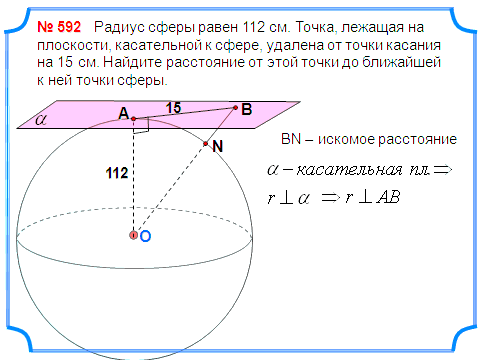
З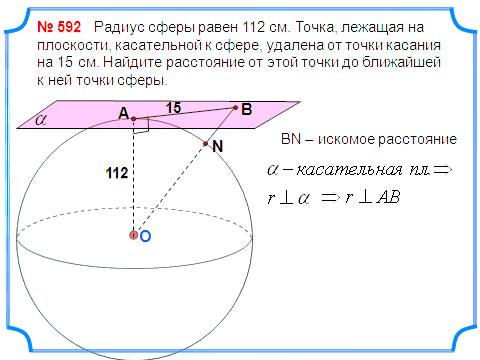 адача 3. Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.
адача 3. Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.
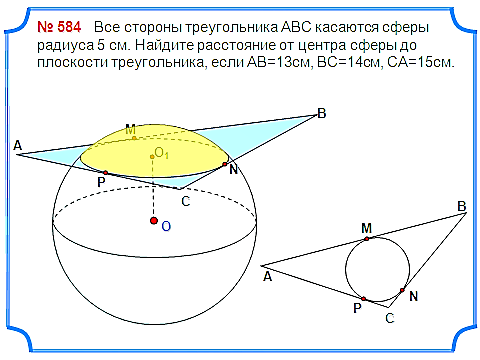
Задача 4. Все стороны треугольника АВС касаются сферы радиуса 5 см. Найдите расстояние от центра сферы до плоскости треугольника, если АВ=13см, ВС=14см, СА=15см.
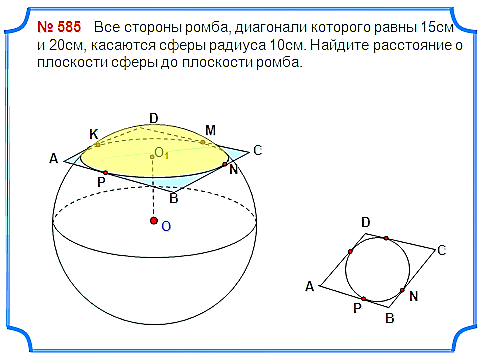
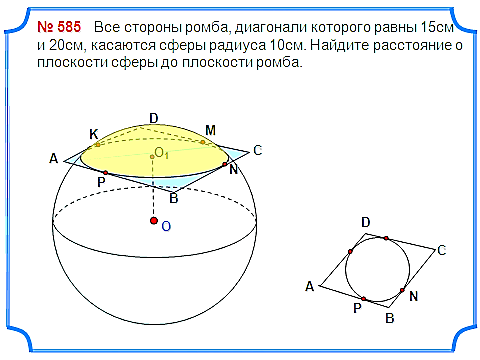
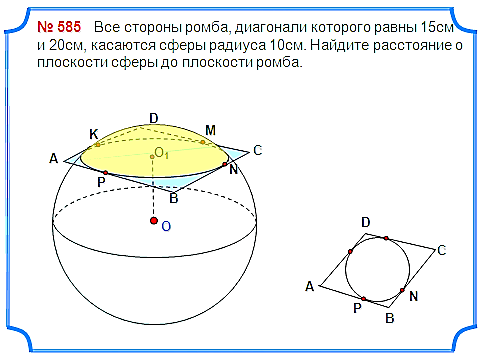
Задача 5. Все стороны ромба, диагонали которого равны 15см и 20см, касаются сферы радиуса 10см. Найдите расстояние о плоскости сферы до плоскости ромба.
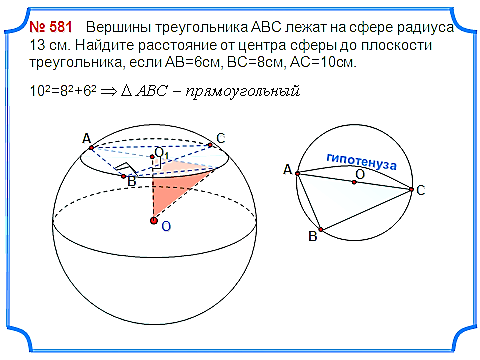
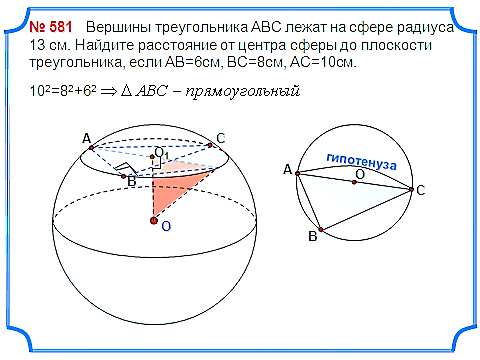
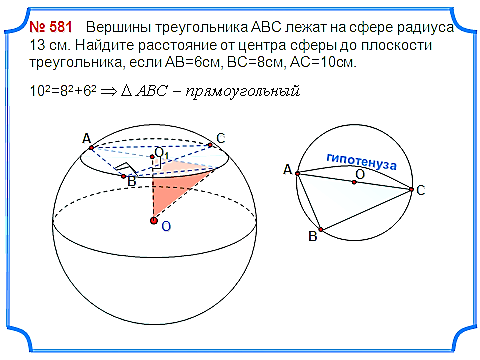
Задача 6. Вершины треугольника АВС лежат на сфере радиуса 13 см. Найдите расстояние от центра сферы до плоскости треугольника, если АВ=6см, ВС=8см, АС=10см.
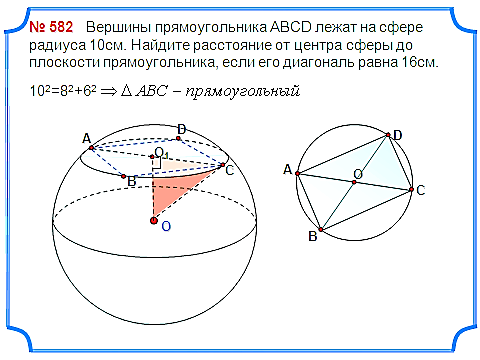
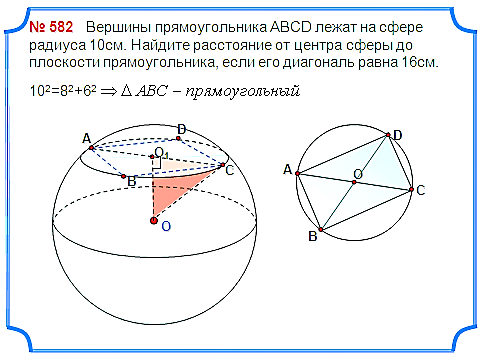
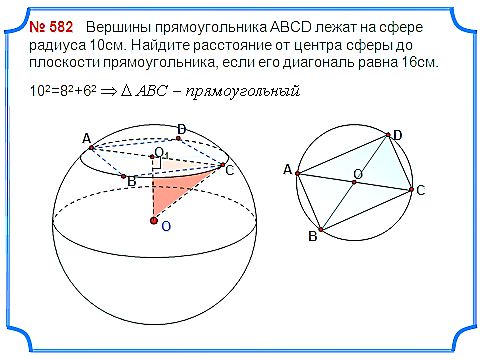
Задача 7. Вершины прямоугольника АВСD лежат на сфере радиуса 10см. Найдите расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16см.
















 фера и плоскость имеют одну общую точку
фера и плоскость имеют одну общую точку





 адача 3. Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.
адача 3. Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.







 фера и плоскость имеют одну общую точку
фера и плоскость имеют одну общую точку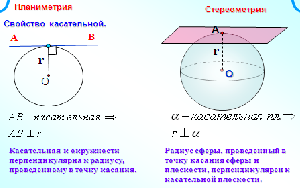

 адача 3. Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.
адача 3. Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.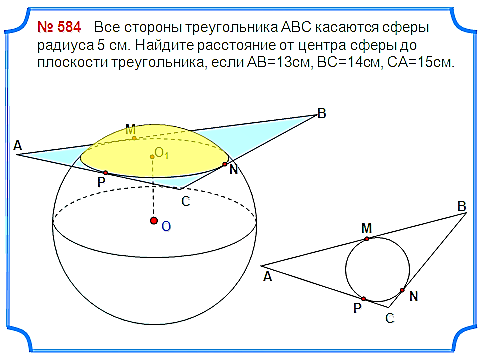




 фера и плоскость имеют одну общую точку
фера и плоскость имеют одну общую точку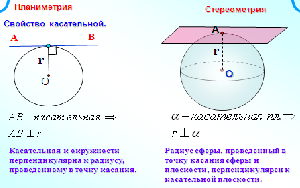
 адача 3. Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.
адача 3. Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.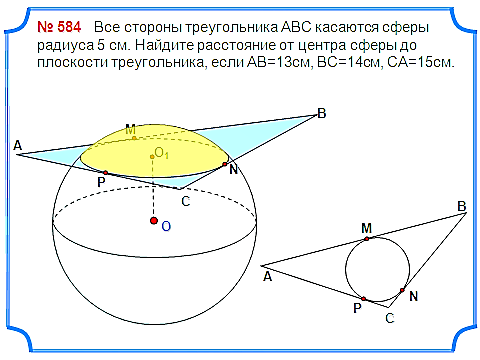
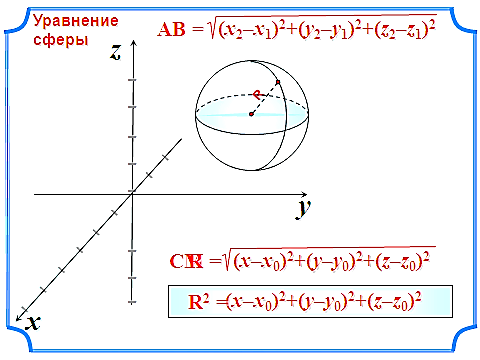
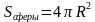 , где
, где 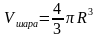 .
.


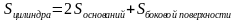
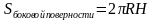
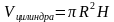
 ешение задач
ешение задач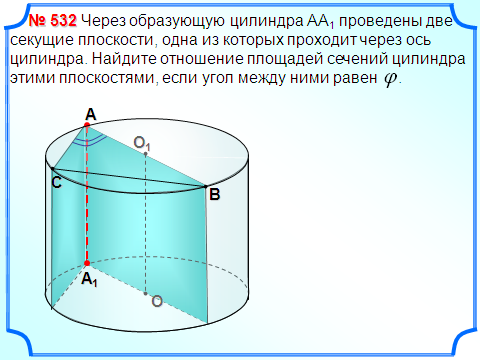 адача 2
адача 2 адача 3.
адача 3.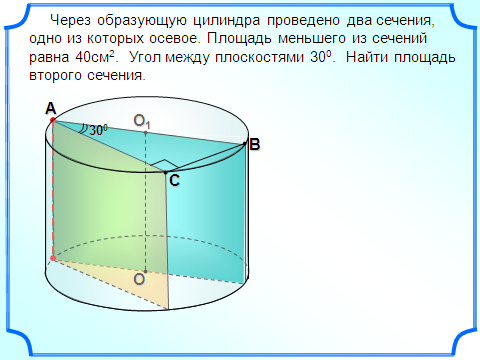 адача 4.
адача 4.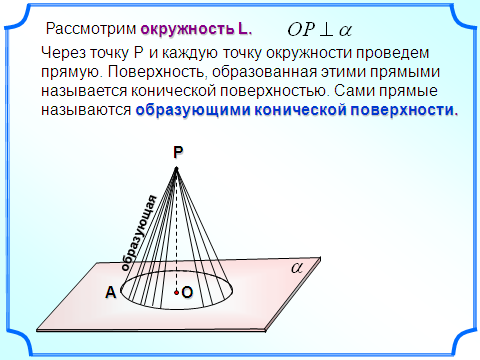
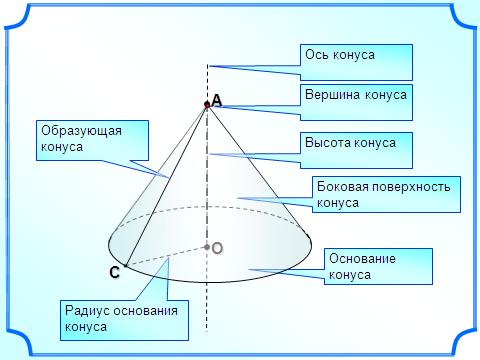
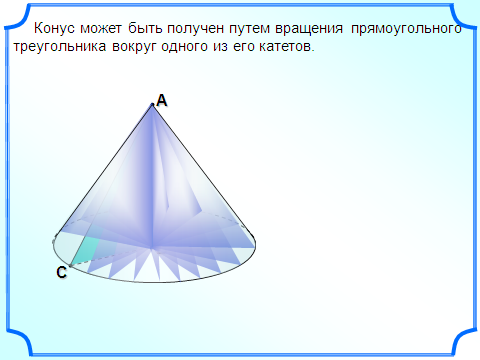
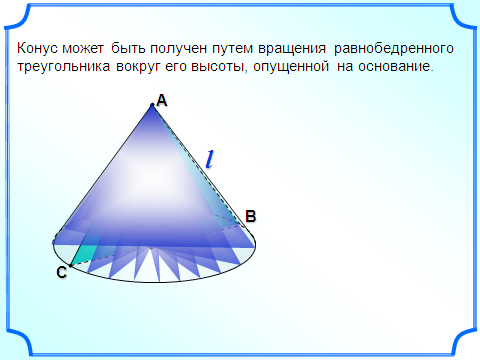 пособ 2.
пособ 2. 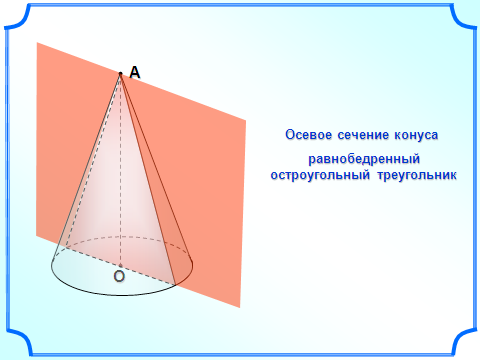
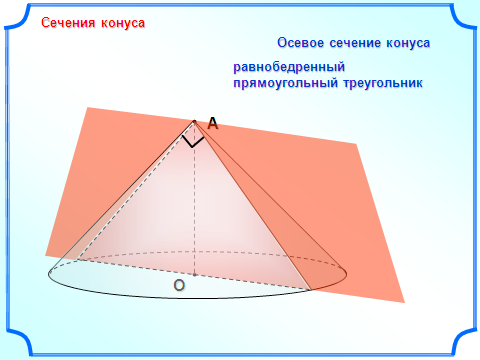
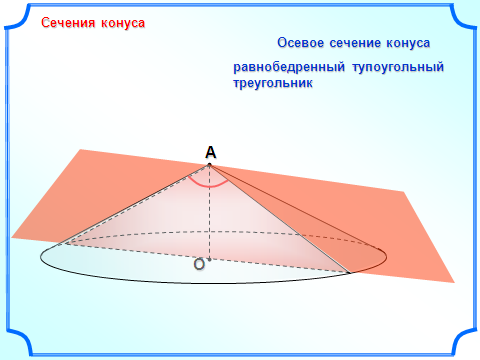
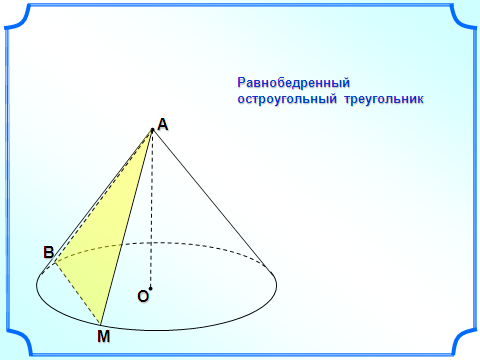
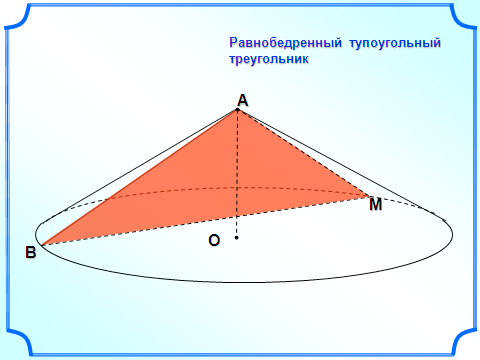
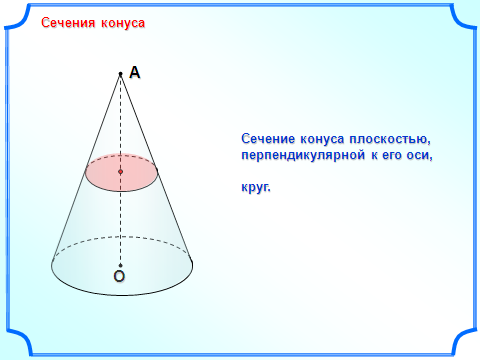
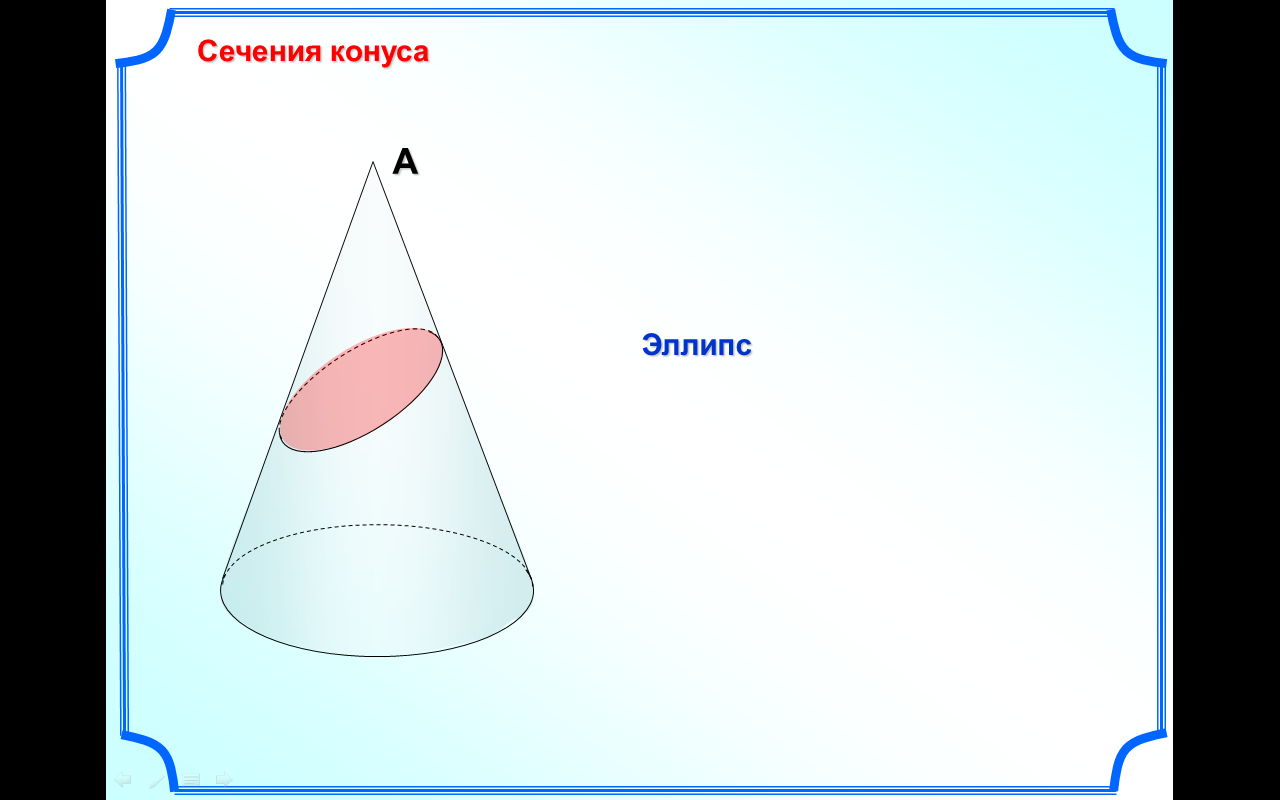
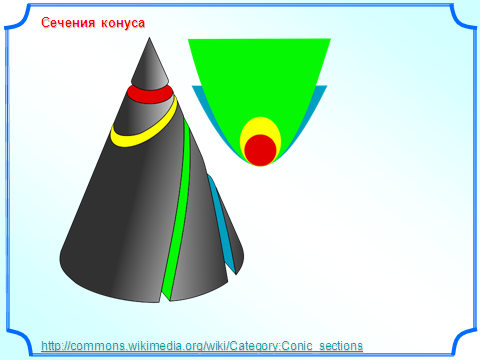
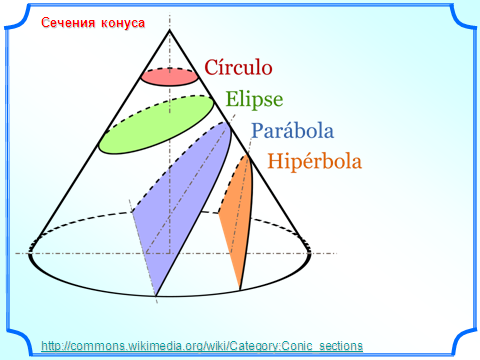
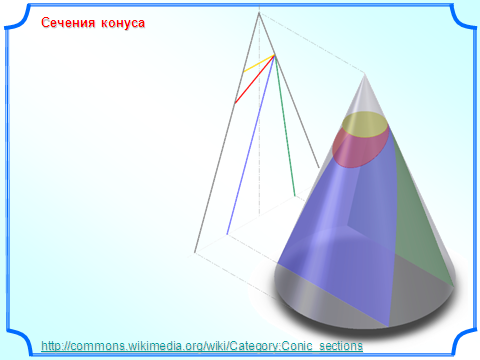
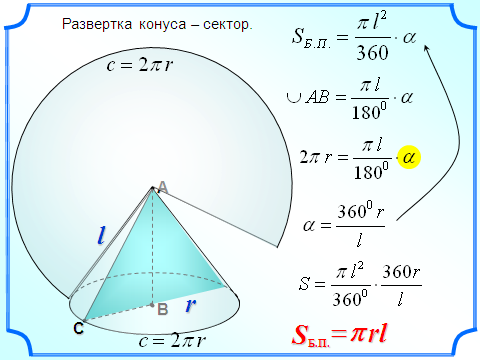
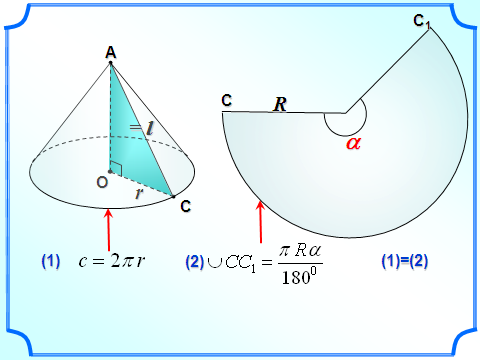
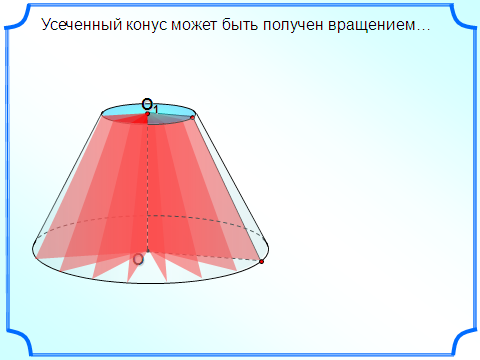
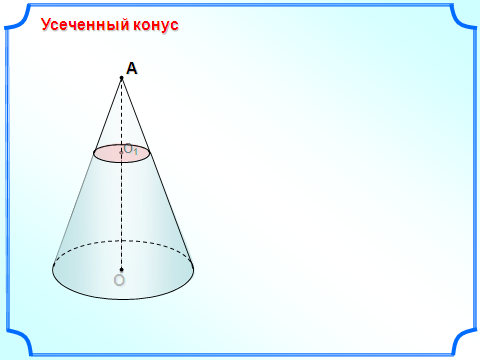 сеченным конусом называется геометрическое тело, ограниченное боковой поверхностью конуса, его основанием и секущей плоскостью α, перпендикулярной оси конуса.
сеченным конусом называется геометрическое тело, ограниченное боковой поверхностью конуса, его основанием и секущей плоскостью α, перпендикулярной оси конуса.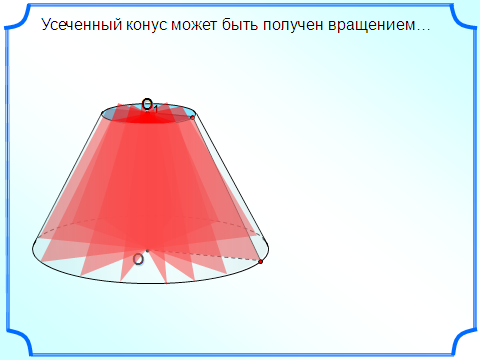
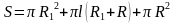
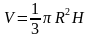

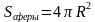 , где
, где 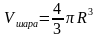 .
.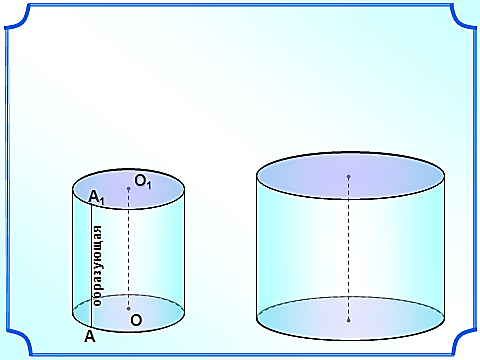
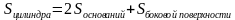
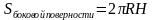
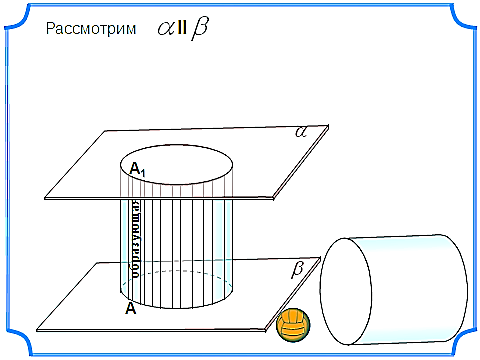
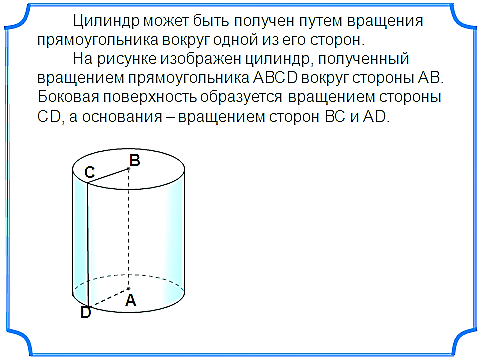
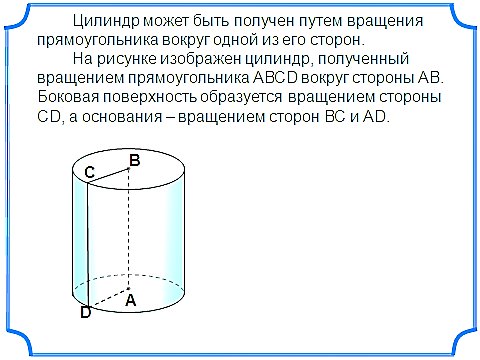 а объем цилиндра, принимается число, к которому стремится объем правильной призмы, вписанной в цилиндр, когда число сторон ее оснований неограниченно возрастает
а объем цилиндра, принимается число, к которому стремится объем правильной призмы, вписанной в цилиндр, когда число сторон ее оснований неограниченно возрастает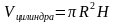
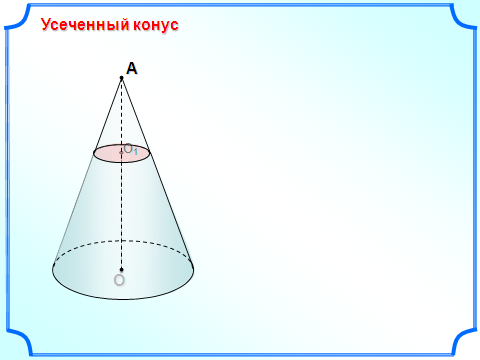 сеченным конусом называется геометрическое тело, ограниченное боковой поверхностью конуса, его основанием и секущей плоскостью α, перпендикулярной оси конуса.
сеченным конусом называется геометрическое тело, ограниченное боковой поверхностью конуса, его основанием и секущей плоскостью α, перпендикулярной оси конуса.