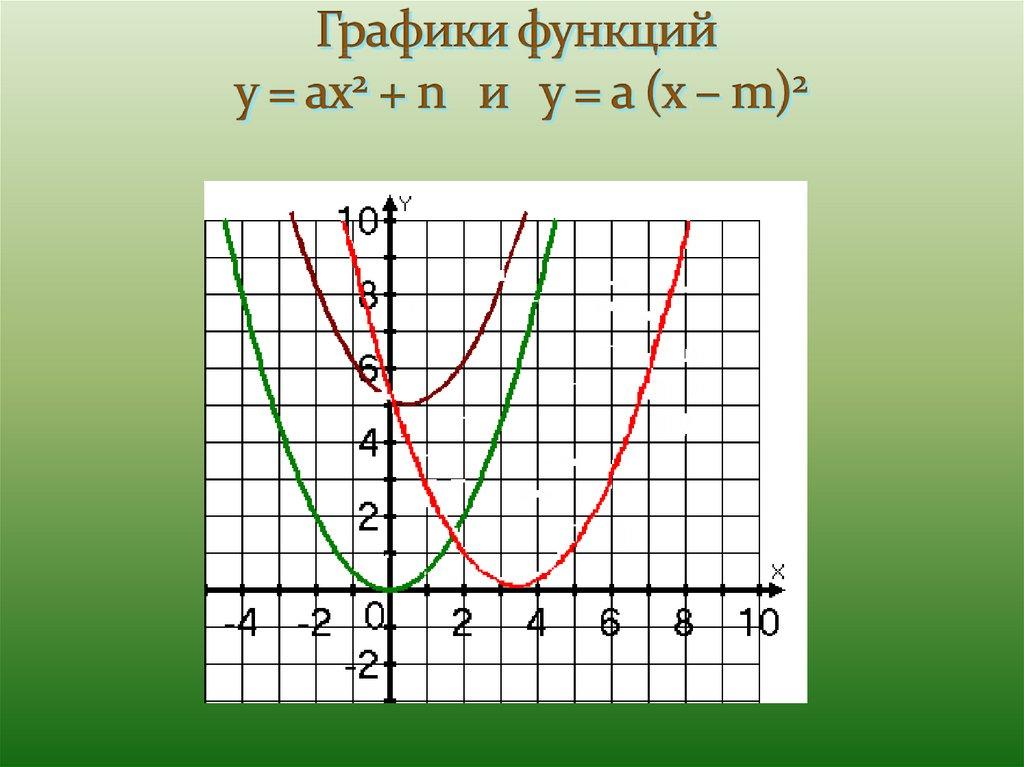
Тема: «Графики функций y = ax2+ n и y = a(x-m)2»
Цели: 1.Научить изображать схематически графики функций y= ах²+n и y=а(х-m)² с помощью параллельного переноса вдоль осей координат.
2.формирование умений строить график квадратичной функции (частные случаи), определять свойства функции по графику, применять шаблоны парабол.
3.Строить с помощью шаблона графики функций.
4.Развивать интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание.
5.Воспитывать волю, внимательность, логическое мышление на всех этапах урока
Оборудование: карточки, шаблоны парабол.
Тип урока: урок объяснения нового материала.
Формы работы: фронтальная, парная, индивидуальная.
Методы: словесные, наглядные; эвристическая беседа; репродуктивный, частично-поисковый.
Планируемые результаты: - развить умения у учащихся
-
систематизировать знания о графиках функций, их свойствах;
-
устанавливать соответствие между графиком и формулой;
-
делать обобщения и выводы.
ПЛАН УРОКА
-
Организационный момент
-
Устная работа (повторение свойств квадратичной функции)
-
Изучение нового материала
-
Закрепление изученного материала
-
Проверка знаний: самостоятельная работа
-
Подведение итогов урока
-
Домашнее задание.
ХОД УРОКА
-
Организационный момент
-Здравствуйте, ребята! Сегодня на уроке мы расширим свои знания о свойствах квадратичной функции, а так же познакомимся с графиками частных видов квадратичной функции: у = ах2, у = ах2 + n, y = a (x – m)2; у=a (x – m)2 +n.
Начать урок мне хотелось бы с китайской пословицы, которая гласит:
«Я слушаю, – я забываю;
Я вижу, – я запоминаю;
Я делаю, – я усваиваю»
-Я желаю вам успешной работы на уроке!
2. Устная работа (слайды)
-
определить коэффициент a по графику функции.
-
назвать нули функции
-
определить y0 и y по графику функции.
-
назвать промежутки возрастания и убывания функции.
-
назвать наибольшее или наименьшее значение функции.
-
посмотреть на график функции у =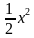 и перечислите его свойства?
и перечислите его свойства?
3. Изучение нового материала:
Рассмотрим частные случаи квадратичной функции вида  и
и 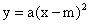 на примере функций
на примере функций
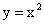
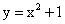

для этого сравним значения этих функций с помощью таблиц значений

Правило: график функции y = ax2+ n является параболой, которую можно получить с помощью параллельного переноса вдоль оси y на n единиц вверх, если n0, или на –n единиц вниз, если n
Теперь рассмотрим функции
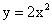


таблицы значений функций
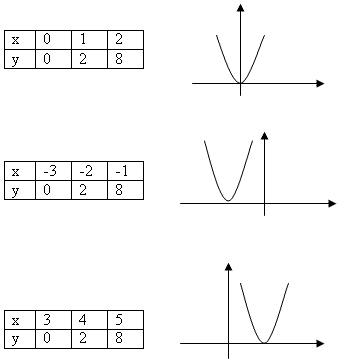
Правило: график функции 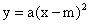 является параболой, которую можно получить с помощью параллельного переноса вдоль оси X на m единиц вправо, если m0, или на – m единиц влево, если m
является параболой, которую можно получить с помощью параллельного переноса вдоль оси X на m единиц вправо, если m0, или на – m единиц влево, если m
4. Закрепление изученного материала
Устно.
Задания на соотнесения.
-
Какому графику соответствует функция, заданная формулой y = x2 – 2?

2. Функция задана формулой. Соотнесите график функции с её формулой заполнив таблицу.
1) у = 2(х + 1)² - 3 2) у = 2(х + 3)² + 1 у = 2(х - 1)² - 3.
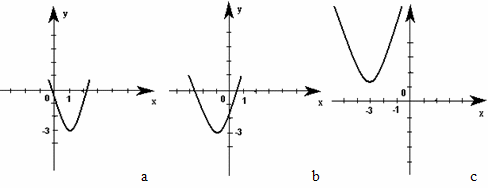
-
Укажите график функции, соотнеся их с формулой, и прочитай полученное слово:
1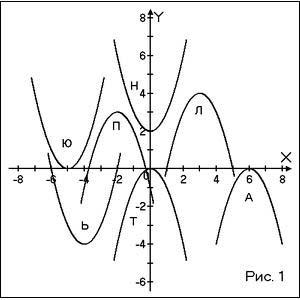 ) y = –x²;
) y = –x²;
2) y = (x+5)²;
3) y = –(x–3)²+4;
4) y = (x+4)²–4;
5) y = –(x+2)²+3;
6) y = –(x–6)²;
7) y = x²+2.
Работа с учебником
-
№ 87(а, г) – дети выполняют у доски и тетрадях
-
№ 88 - использовать шаблон параболы, проверка
5.Проверка знаний: самостоятельная работа
Используя шаблоны парабол y=2x2; y=3x2, постройте графики функций.
I. Вариант II. Вариант
1. y = 2x2 1. y = 3x2
2. y = 2 (x-2)2+1 2. y = 3 (x-2)2+1
3. y = -2 (x-2)2 3. y = 3(x-3)2-3
4. y = 2 (x+4)2 -2 4. y = -3(x-4)2+2
5. y = -2 (x-5)2+3 5. y = -3(x-5)2-1
6. Подведение итога урока
- С какими частными случаями квадратичной функции мы познакомились сегодня на уроке?
7.Домашнее задание:
№ 89, № 87(б,в)
М КОУ «Гимназия им. М.Горького»
КОУ «Гимназия им. М.Горького»
Урок по алгебре на тему:
«Графики функций y = ax2+ n и y = a(x-m)2»

Подготовила и провела: учитель математики
Арсланалиева Гёзель Акавовна, 9 «а» класс
2019 год






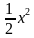 и перечислите его свойства?
и перечислите его свойства? 
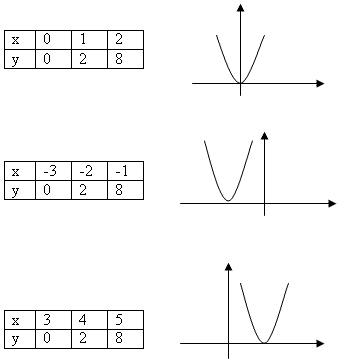


 ) y = –x²;
) y = –x²; КОУ «Гимназия им. М.Горького»
КОУ «Гимназия им. М.Горького»




















