Тема. Понятие множества. Мощность множества. Операции над множествами.
Теория множеств — основа многих разделов математики
Не новость, что информатика неразрывно связана с математикой, одним из фундаментальных понятий которой является понятие множества. Теория множеств стала основой многих разделов математики — общей топологии, общей алгебры, функционального анализа и оказала существенное влияние на современное понимание предмета математики. Так же теория множеств помогает в понимании логических основ информатики.
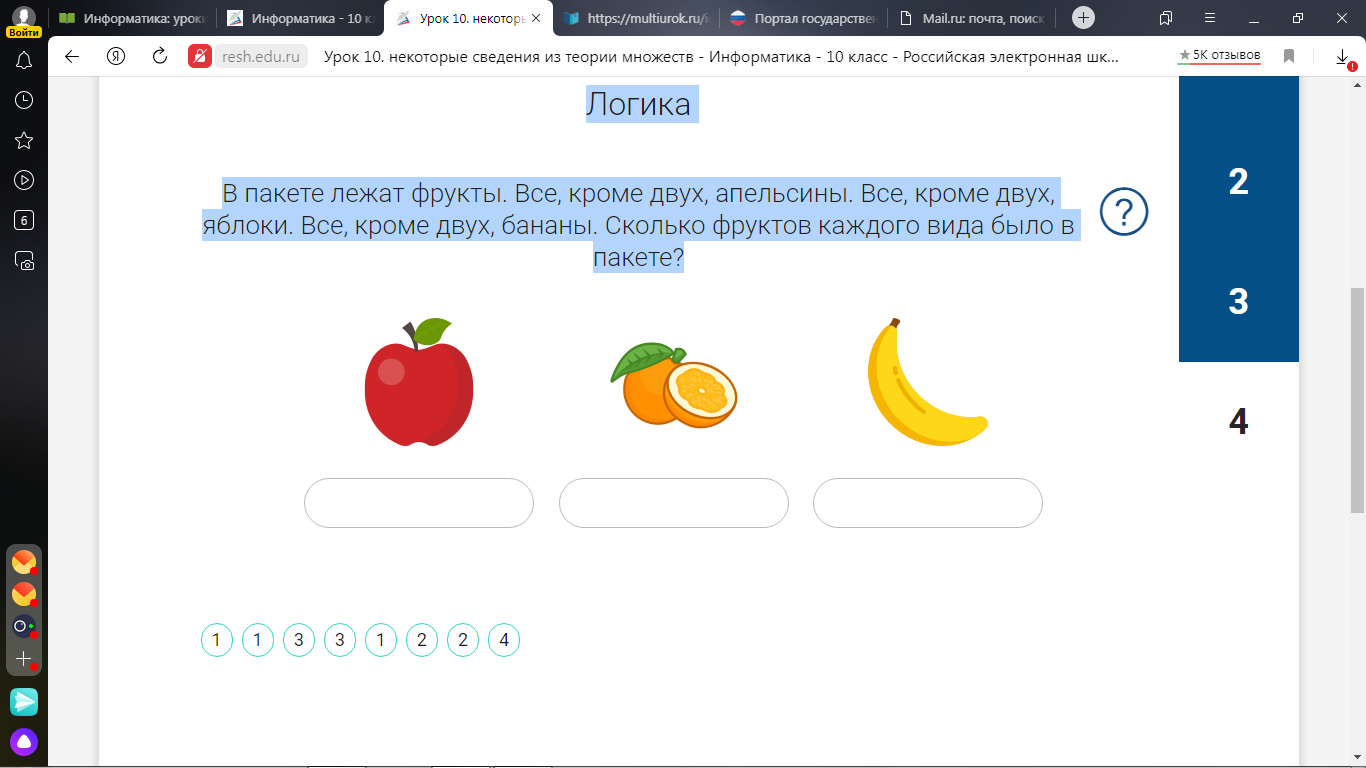
Логика
В пакете лежат фрукты. Все, кроме двух, апельсины. Все, кроме двух, яблоки. Все, кроме двух, бананы. Сколько фруктов каждого вида было в пакете?
1. ПОНЯТИЕ МНОЖЕСТВА
Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором, создателем теории множеств.
 Георг Кантор (1845—1918)
Георг Кантор (1845—1918)
Множеством называется совокупность определенных вполне различаемых объектов, рассматриваемых как единое целое. Создатель теории множеств Георг Кантор давал следующее определение множества — «множество есть многое, мыслимое нами как целое». Отдельные объекты, из которых состоит множество, называются элементами множества.
Комбинаторика. - это раздел математики, посвященный решению задач выбора и расположения элементов некоторого, как правило, конечного множества в соответствии с заданными правилами.
Элементы комбинаторики: размещение, сочетание, перестановки и комбинации с повторением. Элементы комбинаторики – это разные подмножества, которые образованы из каких-нибудь элементов и отличаются друг от друга, либо самими элементами, либо порядком их расположения, называются соединениями. Элементы, из которых образовываются соединения и обозначаются буквами a, b, c, ….
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое. Под множеством мы можем понимать: учеников класса, фрукты, деревянные предметы, числа и т. д.
Например:
| Маша, Петя, Валя, Коля … | Множество учеников класса |
| Стол, стул, карандаш, доска … | Множество деревянных предметов |
| 1, 2, 5, 7, 9 … | Множество чисел |
| Яблоко, банан, арбуз … | Множество фруктов |
Множества принято обозначать прописными буквами латинского алфавита (A,B,C,D и т. д.).
| Множество учеников класса | A |
| Множество деревянных предметов | B |
| Множество чисел | C |
| Множество фруктов | D |
Множество можно задать перечислением всех его элементов, заключенных в фигурные скобки:
| Множество учеников класса | Множество фруктов |
| A={Маша, Ваня, Петя….} | D ={Банан, яблоко, виноград….} |
| Множество деревянных предметов | Множество чисел |
| B ={миска, подставка под карандаши, разделочная доска….} | C ={1,2,3,4,5….} |
Из некоторых элементов одного множества можно составить новое. Тогда такое множество Е принято называть подмножеством D:
D={1,2,3,4,5,6,7,8…}
E={2,4,6,8…}
Для наглядности множества можно изображать в виде окружности, так называемых кругов Эйлера, где элементы, входящие в множество, изображают внутри круга, а остальные вне.
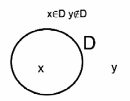
1)Пересечением множеств называется множество их общих элементов.
Например:
Пусть множество A будет состоять из элементов 1,3,6,9,12,15, а множество B из элементов 2,4,6,8,10,12. Тогда в пересечение этих множеств будет входить 2,6,12:
| 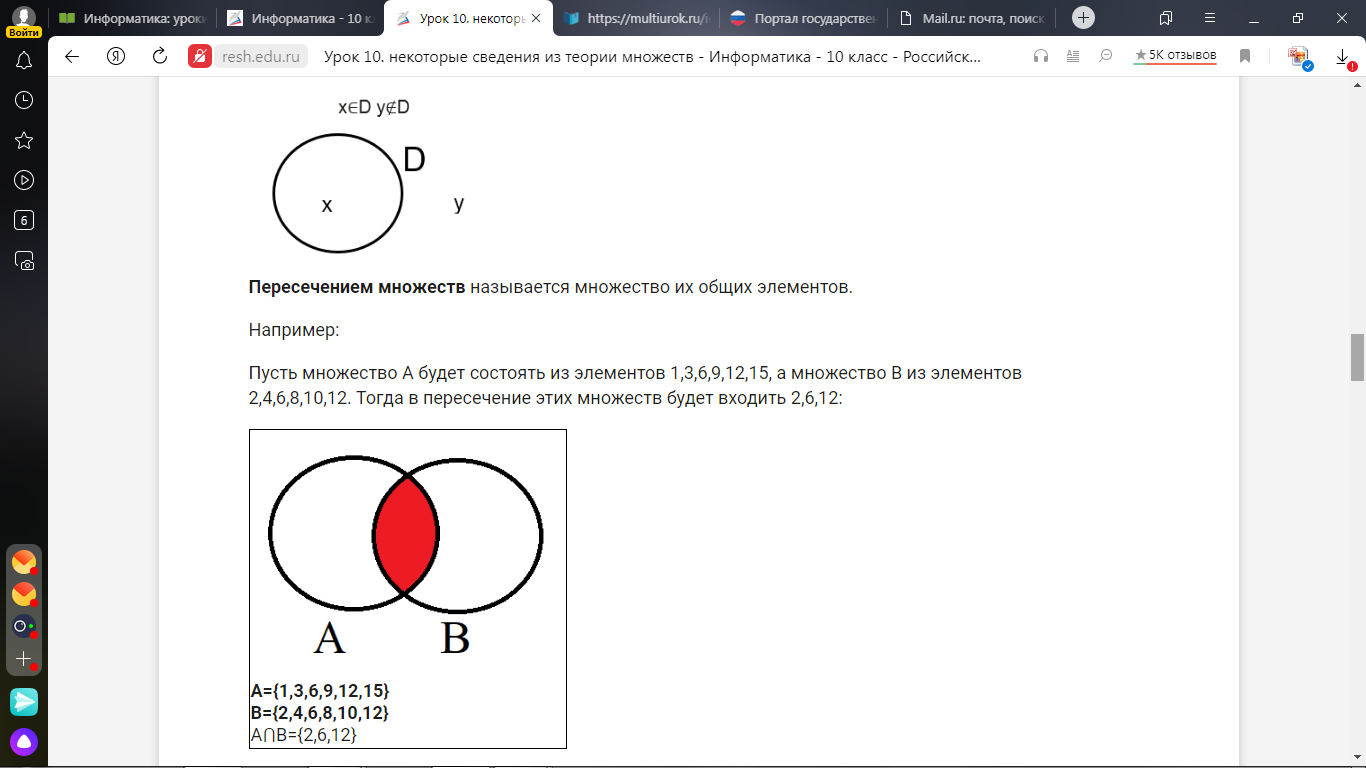
| A={1,3,6,9,12,15} B={2,4,6,8,10,12} A⋂B={2,6,12} |
2)Множество может не содержать элементы, тогда оно будет называться пустым.
Если множества не имеют общих элементов, то их пересечение — пустое множество:
| 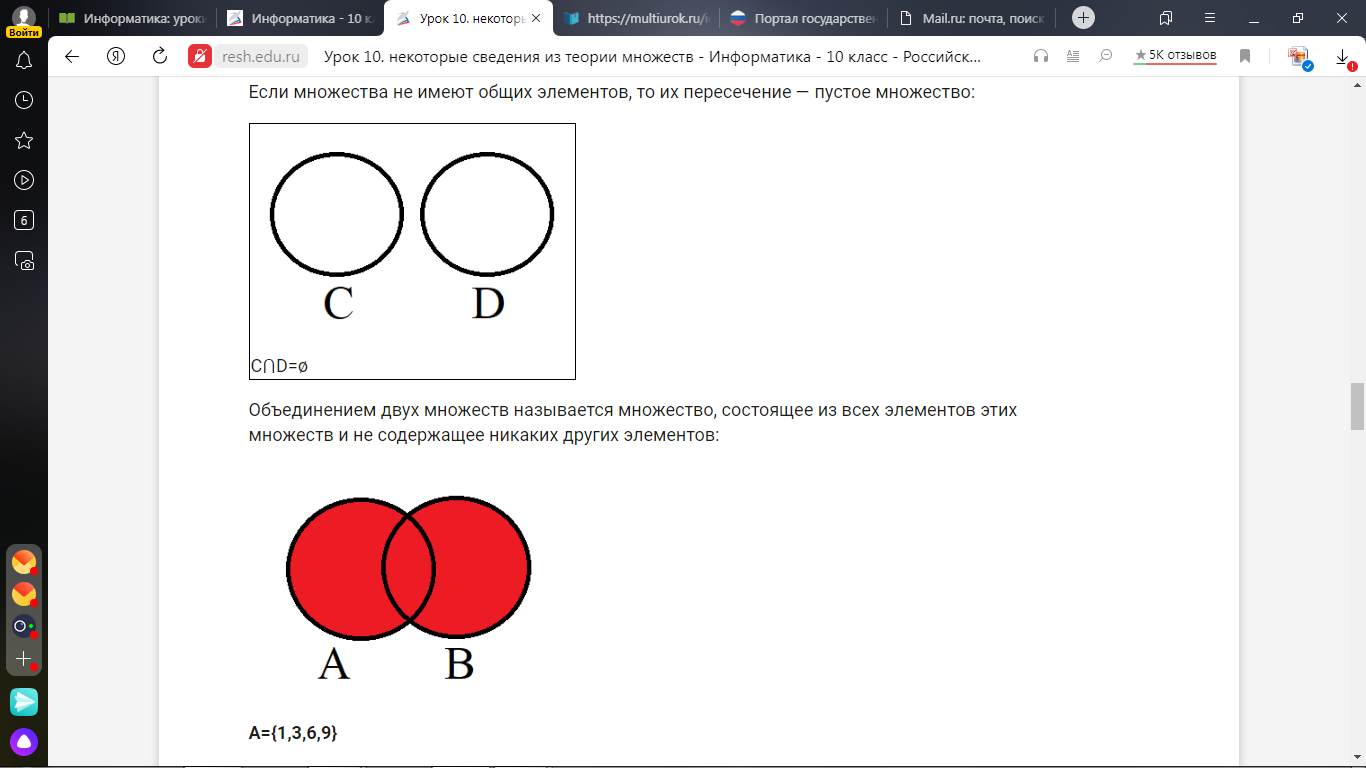
| С⋂D=ø |
3) Объединением двух множеств называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов:
| 
| A={1,3,6,9} B={2,4,6,8} A⋃B={1,2,3,4,6,8,9} |
4) Разностью множеств А и В называется множество элементов, принадлежащих множеству А, которые не принадлежат множеству В:
| 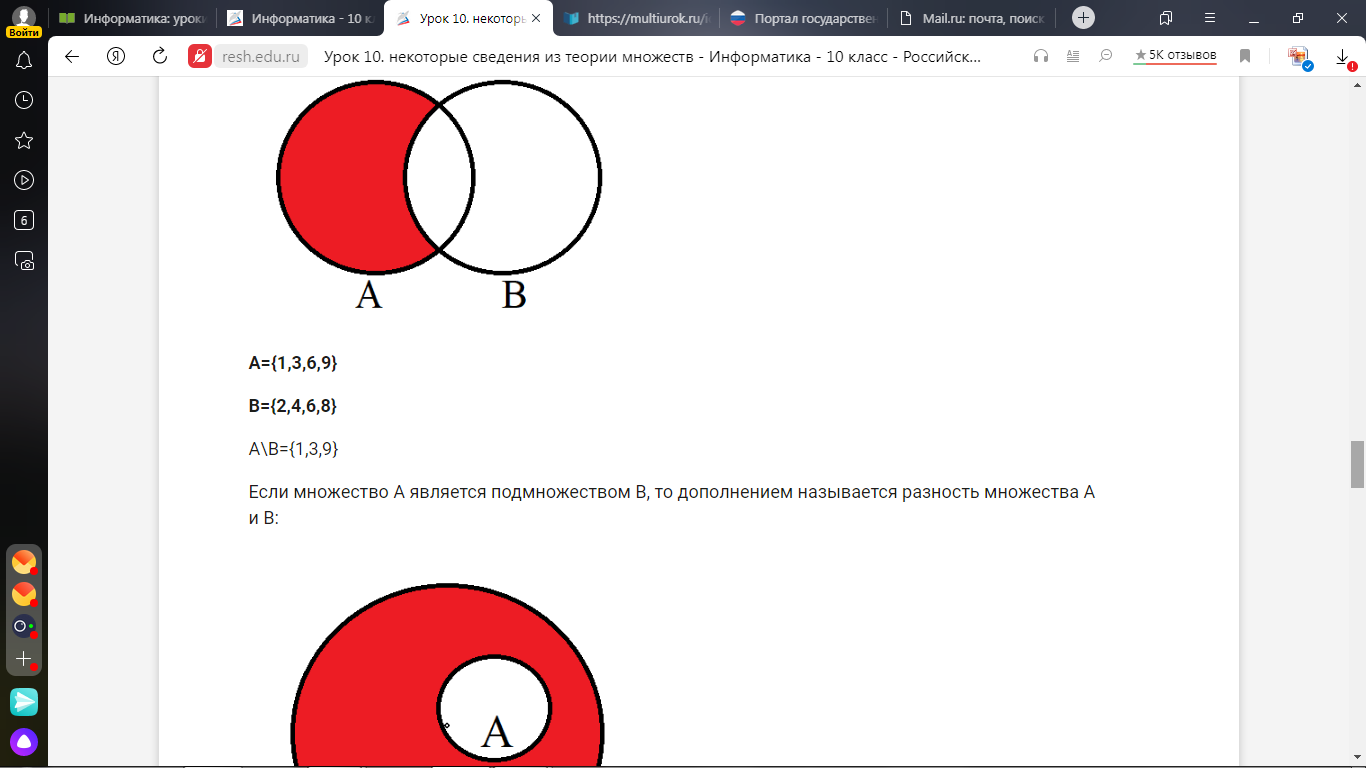
| A={1,3,6,9} B={2,4,6,8} A\B={1,3,9} |
5) Если множество А является подмножеством B, то дополнением называется разность множества А и В:
| 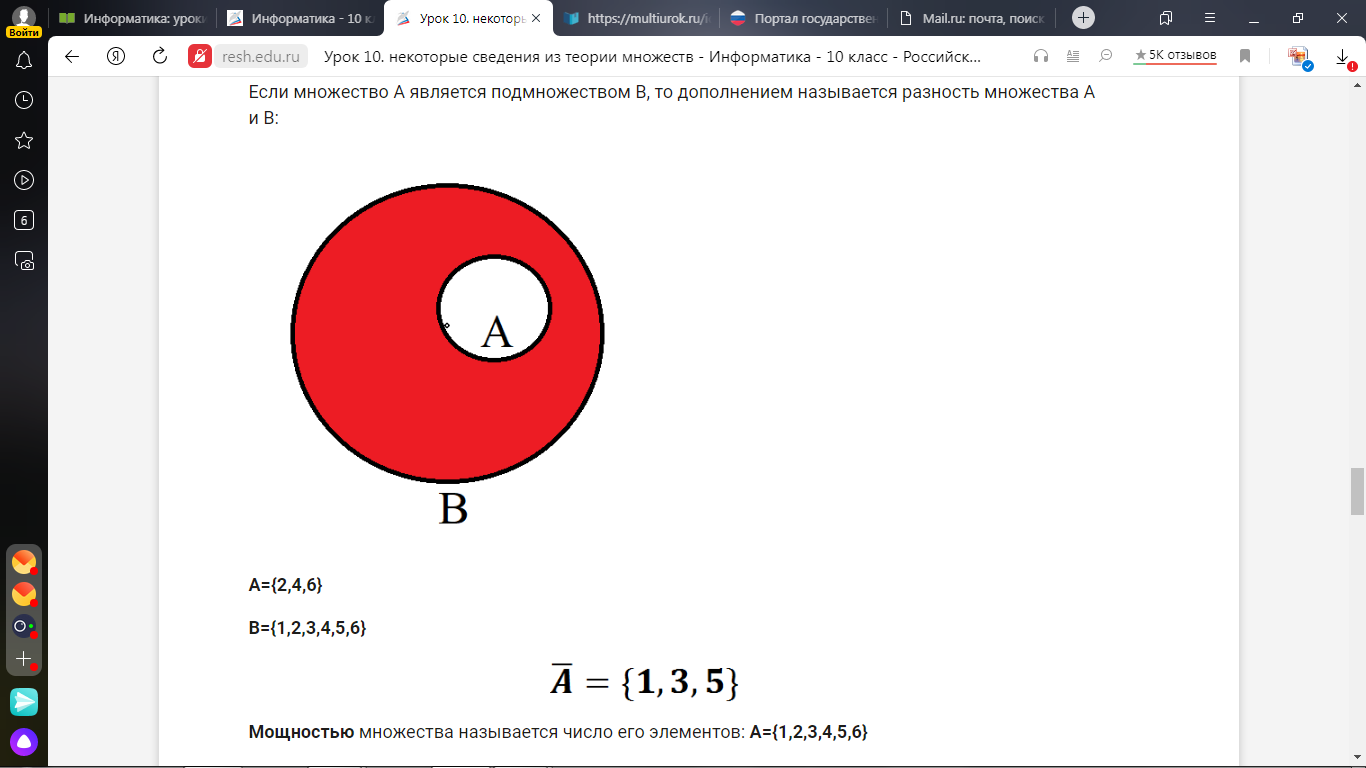
| A={2,4,6} B={1,2,3,4,5,6} Ā={1,3,5} |
Работа студентов у доски под руководством преподавателя
Задание №1
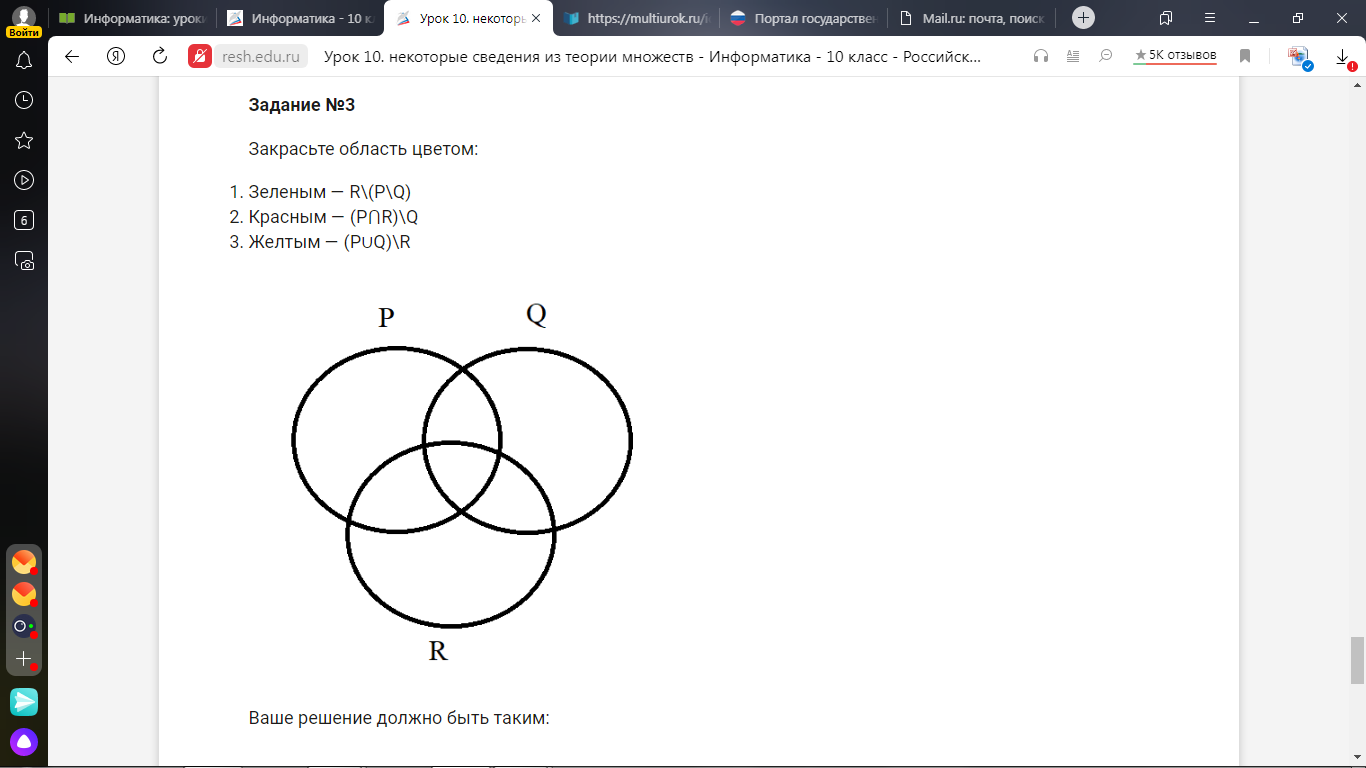
| Закрасьте следующие области цветом: Зеленым — R\(P\Q) Красным — (P⋂R)\Q Желтым — (P∪Q)\R
| 
|
Задание №2
Элементы множества и диаграммы
Установите соответствие между множеством и закрашенной областью на диаграмме.
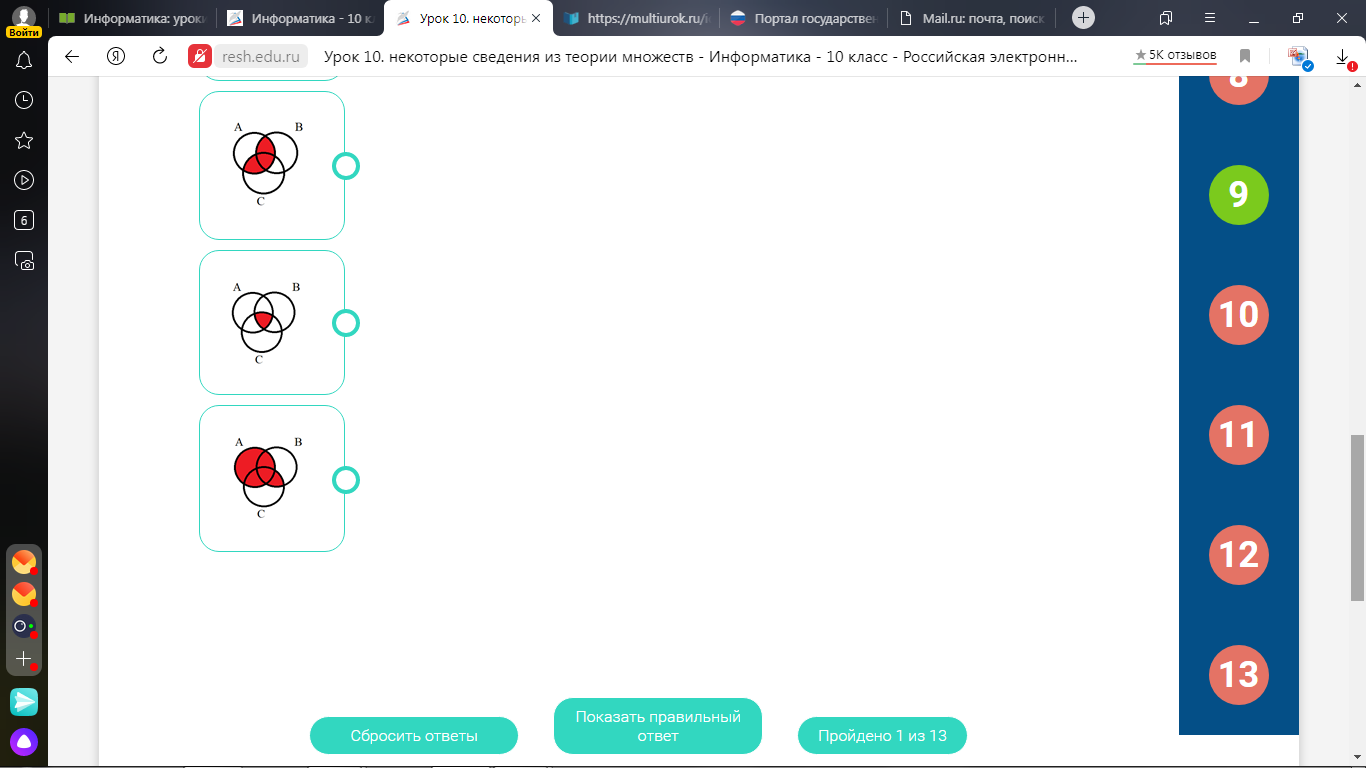
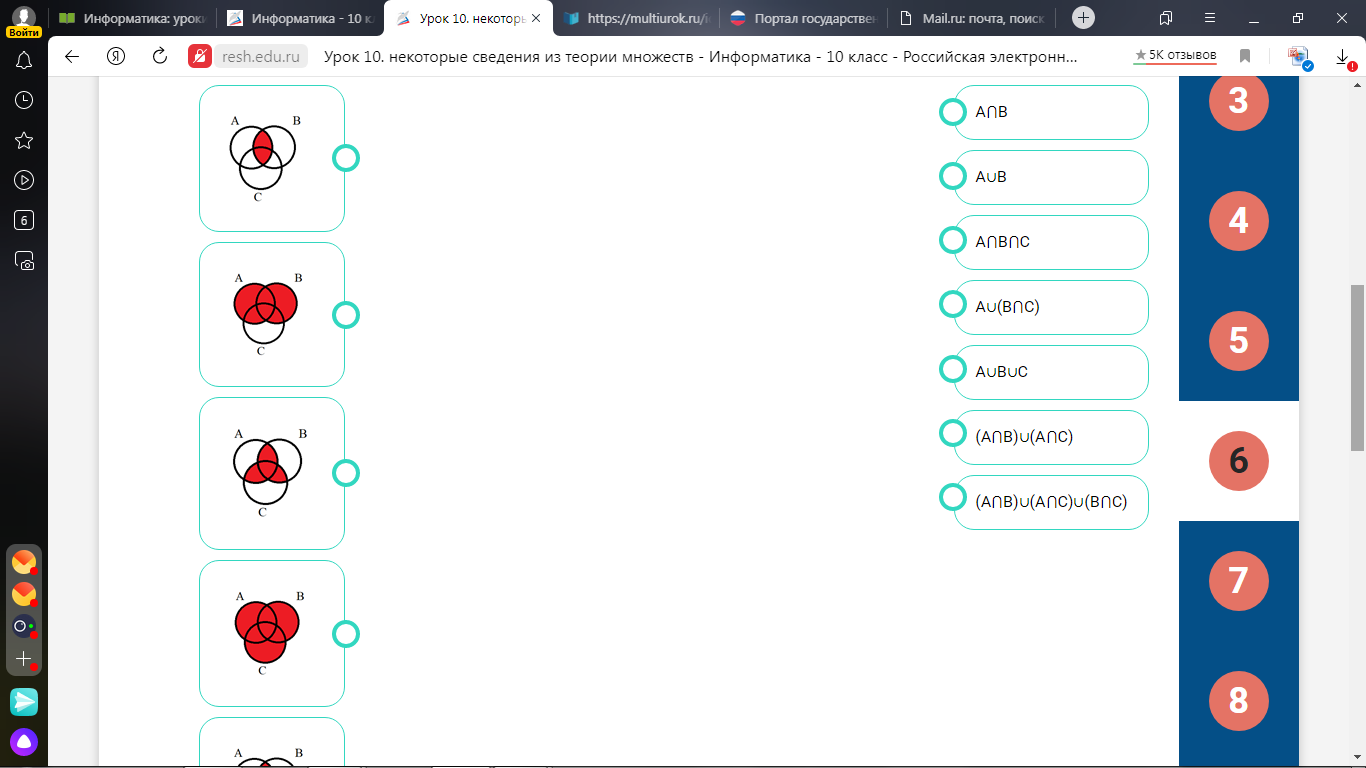
2. МОЩНОСТЬ МНОЖЕСТВА
Мощностью множества называется число его элементов:
A={1,2,3,4,5,6}
|A|=5
Таким образом, мощность непересекающихся множеств будет являться суммой мощностей каждого множества:
A={1,3,5,7}
B={2,4,6,8}
|A⋃B|=8
Для вычисления мощности пересекающихся множеств можно использовать принцип включений и исключений:
|A⋃B|= |A|+|B|–| A⋂B|
A={1,2,3,4,5,6}
B={2,4,6,8}
|A⋃B|=6+4–3=7
Для вычисления мощности пересечения трех множеств принцип включений и исключений выглядит так:
|A⋃B⋃С|= |A|+|B|+|C|–|A⋂B|–|A⋂C|-|B⋂C|+|A⋂B⋂C|
Пример преподавателя на маркерной доске
Задача.
В классе 17 пловцов, 8 борцов и 13 футболистов. Известно, что в классе 25 детей, а ребят занимающихся футболом и плаваньем — 10, борьбой и плаваньем — 3, борьбой и футболом — 2 и только один ребенок занимается всеми тремя видами спорта. Сколько детей в классе не занимаются спортом?
Дано:
|A|=17, |B|=8, |C|=13
|A⋂B|=3, |A⋂C|=10, |B⋂C|=2
|A⋂B⋂C|=1
по формуле включения:
|A⋃B⋃С|= |A|+|B|+|C|–|A⋂B|–|A⋂C|–|B⋂C|+|A⋂B⋂C|=17+8+13–3–10–2+1=24
Таким образом, в классе 24 ребенка занимаются хотя бы одним видом спорта, следовательно: 25 – 24 = 1
ответ 1
Работа студентов у доски под руководством преподавателя
Задание №3
Мощность множества
Используя данные из таблицы, найдите мощность множества L⋂K.

 L⋂K = …
L⋂K = …
ВАЖНО! Подведем итоги
Понятие множества является одним из наиболее общих и наиболее важных математических понятий.
Множество – это совокупность объектов произвольной природы, которая рассматривается как единое целое.
Под множеством мы можем понимать: учеников класса, фрукты, деревянные предметы, числа и т.д.
Множество можно задать перечислением всех его элементов, заключенных в фигурные скобки.
Из некоторых элементов одного множества можно составить новое.
Тогда такое множество Е принято называть подмножеством D.
Для наглядности множества можно изображать в виде окружности, так называемых кругов Эйлера, где элементы, входящие в множество, изображают внутри круга, а остальные вне.
Пересечением множеств называется множество их общих элементов.
Множество может не содержать элементы, тогда оно будет называться пустым.
Мощностью множества называется число его элементов.
Мощность непересекающихся множеств будет являться суммой мощностей каждого множества.
4








 Георг Кантор (1845—1918)
Георг Кантор (1845—1918) 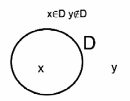








 L⋂K = …
L⋂K = …









