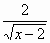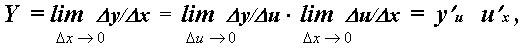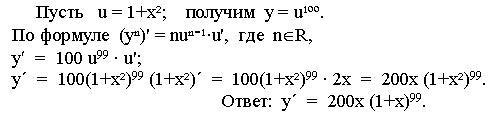Предмет: математика
Преподаватель: Амирханова А.К.
Тема: “Производная сложной функции”.
Тип урока: – урок изучения нового материала.
Форма урока: применение информационных технологий.
Цели:
научить распознавать сложные функции, уметь применять правила вычисления производных; совершенствовать предметные, в том числе вычислительные, умения и навыки; навыки работы с компьютером;
развивать готовность к информационно-учебной деятельности через применение информационных технологий.
воспитывать адаптивность к современным условиям обучения.
Ход урока.
I. Организационный момент (0.5 мин.).
II. Постановка целей. Мотивация учащихся (1 мин.).
Обучающие цели: научиться распознавать сложные функции, знать правила дифференцирования, уметь применять формулу производной сложной функции при решении задач; совершенствовать предметные, в том числе вычислительные, умения и навыки; навыки работы с компьютером.
Развивающие цели: развивать познавательные интересы через применение информационных технологий.
Воспитательные цели: воспитывать адаптивность к современным условиям обучения.
III. Актуализация опорных знаний (5 мин.).
Дать определение производной функции.
Назовите правила вычисления производной.
Устная работа.
Найдите производные функций.
а) y = 2x2 + xі ;
б) f(x) = 3x2 – 7x + 5;
в) f(x) = 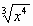 ;
;
г) f(x) = 1/2x2;
д) f(x) = (2x – 5)(x + 3).
4. Правила вычисления производных.
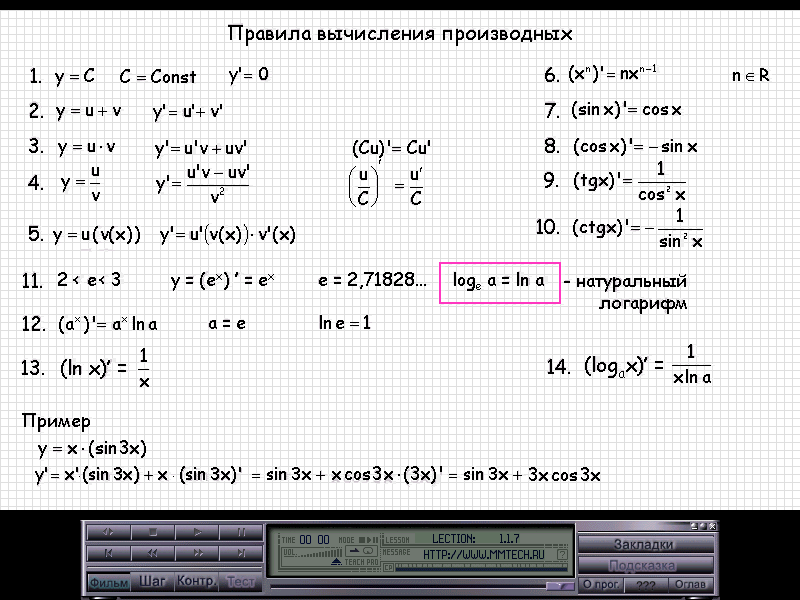
IV. Программированный контроль (5 мин.).
| Найти производную. |
| Вариант 1. | Вариант 2. |
| У = 2х + 5. | У = 2х – 5. |
| У = 4cos x. | у = 3sin x. |
| у = tg x + ctg x. | у = tg x – ctg x. |
| у = 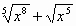 | у = 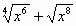 . . |
| У = х2 +7х + 5 | У = 2х2 – 5х + 7 |
| Варианты ответов. |
| 1 | 2 | 3 | 4 |
| 2 | -2 | 5 | -5 |
| 4sin x | -4sin x | 3cos x | -3cos x |
| 1/cos2x + 1/sin2x | 1/cos2x – 1/sin2x | 1/sin2x – 1/cos2x | 1 |
| 1,6х0,6 + 2,5х1,5 | 2,6х0,6 + 1,5х1,5 | 1,5х0,5+ 4х3 | 2,5х0,5+ 4х3 |
| 2х + 7 | 2х +5 | 4х + 5 | 4х – 5 |
Обменяйтесь тетрадями. Отметьте в диагностических картах верно выполненные задания знаком +, а неверно выполненные задания знаком “–”.
V. Новый материал (5 мин.).
Сложная функция.
Рассмотрим функцию, заданную формулой f(x) = 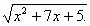
Для того, чтобы найти производную данной функции, надо сначала вычислить производную внутренней функции u = v(x) = xІ + 7x + 5, а затем вычисляют производную функции g(u) = 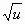 .
.
Говорят, что функция f(x) – есть сложная функция, составленная из функций g и v, и пишут:
f(x) = g(v(x)).
Область определения сложной функции – множество всех тех х из области определения функции v , для которых v(x) входит в область определения функции g.
ТЕОРЕМА.
Пусть сложная функция у = f(x) = g(v(x)) такова, что функция у = v(x) определена на промежутке U , а функция u = v(x) определена на промежутке Х и множество всех её значений входит в промежуток U. Пусть функция u = v(x) имеет производную в каждой точке внутри промежутка Х , а функция y = g(u) имеет производную в каждой точке внутри промежутка U. Тогда функция y = f(x) имеет производную в каждой точке внутри промежутка Х , вычисляемую по формуле
y'x = y'u • u'x.
Формулу читают так: производная y по x равна производной y по u, умноженной на производную u по x.
Формулу записывают ещё так:
f' (x) = g' (u) v' (x).
Доказательство.
В точке х 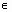 Х зададим приращение аргумента
Х зададим приращение аргумента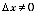 , (х+
, (х+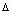 х)
х) 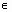 Х. Тогда функция u = v(x) получит приращение
Х. Тогда функция u = v(x) получит приращение 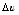 , а функция y = g(u) получит приращение D y. Надо учесть, что, так как функция u=v(x) в точке x имеет производную, то она непрерывна в этой точке и
, а функция y = g(u) получит приращение D y. Надо учесть, что, так как функция u=v(x) в точке x имеет производную, то она непрерывна в этой точке и 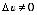 при
при 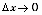 .
.
При условии, что 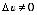 , имеем
, имеем
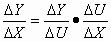 получим
получим
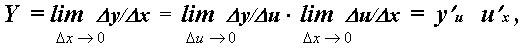
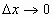
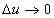
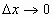
то есть формулу y' x = y' u · u'x .
VI. Закрепление изученного материала (12 мин.).
Применим полученную формулу для решения задач.
Пример 1.
Найти производную функции у = (1+х2)100.
Решение.
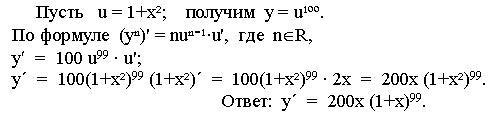
Пример 2 и Пример 3 из учебника (устно разобрать решение).
VII. Примеры для самостоятельного решения (8 мин.).
“Самостоятельная работа”.
у = (х2 – 3х + 1)3 – 1-я группа.
у = (1 + х – 2х2)10 – 1-я группа.
У = (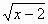 + 2)2 – 2-я группа.
+ 2)2 – 2-я группа.
У = (2 – 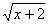 )2 – 2-я группа.
)2 – 2-я группа.
Проверка.
у' = (6х – 9)(х2 – 3х + 1).
у' = (10 – 40х)(1 + х – 2х2).
у' = 1 + 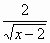
у' = 1 – 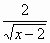
VIII. Индивидуальные задания (7 мин.).
“Индивидуальные задания”.
y = 2x + 3,6 sin5(p - x);
y = sin (2x2 – 3).
y = (1 + sin3x) cos3x;
y = tg x (tg x – 1).
IX. Итог урока (1 мин.).
Дать определение производной функции.
Назовите правила вычисления производных.
Какая функция является сложной?
Какова область определения сложной функции?
Назовите формулу нахождения производной сложной функции.
X. Задание на дом (0.5 мин.).






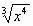 ;
;
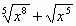
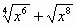 .
.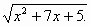
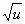 .
.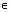 Х зададим приращение аргумента
Х зададим приращение аргумента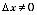 , (х+
, (х+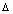 х)
х) 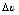 , а функция y = g(u) получит приращение D y. Надо учесть, что, так как функция u=v(x) в точке x имеет производную, то она непрерывна в этой точке и
, а функция y = g(u) получит приращение D y. Надо учесть, что, так как функция u=v(x) в точке x имеет производную, то она непрерывна в этой точке и 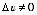 при
при 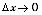 .
.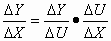 получим
получим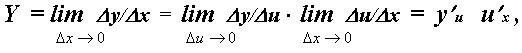
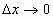
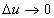
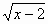 + 2)2 – 2-я группа.
+ 2)2 – 2-я группа.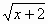 )2 – 2-я группа.
)2 – 2-я группа.