Тема работы: Метод PROMETHEE

Федеральное государственное автономное образовательное учреждение

высшего образования

«БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ»

(НИУ «БелГУ»)

Институт инженерных и цифровых технологий

Кафедра прикладной информатики и информационных технологий

По дисциплине:

Методы и системы поддержки и принятия решений

Тема работы: Метод PROMETHEE

студента очного отделения

4 курса 12001504 группы

Марко С. Тангуила

Проверил:

доц. Путивцева Наталья Павловна 

БЕЛГОРОД, 2019

Цель работы

Приобретение навыков решения задач линейного программирования в табличном редакторе Microsoft Excel.

Результаты выполнения работы

Первая часть лабораторного задания

1. Постановка задачи линейного программирования

Акционерное общество производит и реализует оптовыми партиями соответственно по цене 45 руб. и 30 руб. книги и настольные календари. Постоянные затраты общества (управленческие расходы, содержание офиса и т.п.) составляют 202200 руб. в квартал, переменные затраты (стоимость бумаги, услуги типографии и т.п.) – соответственно 15,75 руб. и 12,3 руб. в расчете на одну книгу и один календарь. Налог на добавленную стоимость составляет 16,67% цены изделия.

Опыт реализации изделий в предыдущие плановые периоды показал, что в течение квартала можно реализовать не более 100000 книг и 40000 календарей.

Требуется на планируемый квартал определить объем производства и реализации изделий (структуру производства и реализации), при котором общество получит максимальную прибыль, а суммарные затраты на производство и реализацию изделий не будут превосходить 2000000 руб.

1. Формирование математической модели

1. Искомые величины.

x₁ и x₂ – объем производства книг и календарей соответственно.

1. Цель решения.

1. Ожидаемая сумма выручки:

1. Затраты на производство:

1. НДС:

1. Прибыль:

1. Ограничения.

1. Суммарные затраты не должны превышать 2000000 руб.

1. В течение квартала можно реализовать не более 100000 книг и 40000 календарей.

1. Объемы производимой продукции должны быть неотрицательными.

1. Объемы производимой продукции должны быть целочисленными.

Таким образом, математическая модель задачи записывается следующим образом:

F=

Упростим:

F=

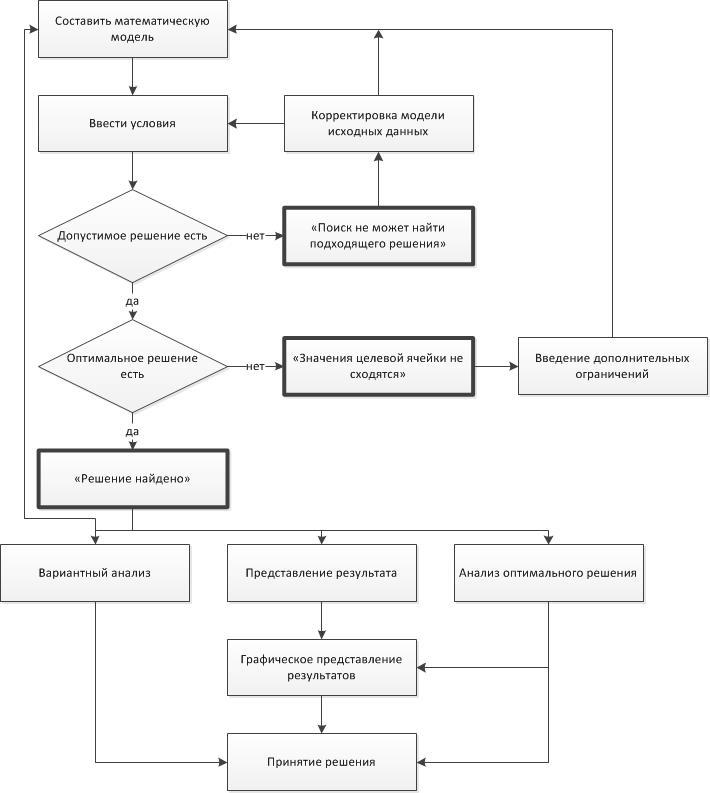
1. Блок-схема задачи

1. Решение задачи в Microsoft Excel

Создала экранную форму для ввода условия задачи, ввела исходные данные, зависимости из математической модели, ограничения и граничные условия (D9=B3*B9+C3*C9, D10=B3, D11=C3) в форму, задала целевую функцию (D6=B6*B3+C6*C3). Установила параметры задачи в окне Поиск решения.

Нашла решение:

1. Решение задачи в Matlab

Основными входными данными linprog являются: С вектор коэффициентов целевой функции f, матрица ограничений-неравенств A, вектор b, ограничивающий план x снизу, вектор ub, ограничивающий план x сверху. На выходе функция linprog даёт оптимальный план x задачи и экстремальное значение целевой функции fval.

Текст программы в Matlab:

function lab1(x)

C= [21.75 12.7];

A = [15.75 12.3];

b = [1797800];

lb = zeros(2,1);

f=C;

ub = [100000 40000];

[x,fval] = linprog(-f,A,b,[],[],lb,ub);

x

fval

Результат решения:

Вторая часть лабораторного задания

Формулировка задачи. Требуется определить, в каком количестве необходимо выпускать продукцию четырех типов П1, П2, П3 и П4, для изготовления которой требуются ресурсы трех видов: трудовые, сырьевые и финансы. Норма расхода, а также прибыль, получаемая от реализации каждого вида продукции, приведены в таблице.

Пусть x₁, x₂, x₃, x₄ – количество каждого из четырех видов продукции; F – целевая функция, которая представляет собой прибыль от реализации произведенной продукции. Математическая модель задачи может быть представлена следующим образом:

В ячейку F6 ввела значение целевой функции =СУММПРОИЗВ(B$3:E$3;B6:E6). Скопировала формулу из ячейки F6 в ячейки F9, F10, F11. Заполнила окно Поиск решения.

Получила решение:

Текст программы в Matlab:

function lab1(x)

C=[60 70 120 130];

A=[1 1 1 1; 6 5 4 3; 4 6 10 13];

b=[16 110 100];

f=C;

lb=zeros(4,1);

[x,fval]=linprog(-f,A,b,[],[],lb);

x

fval

Результат выполнения: