Просмотр содержимого документа
«Тема: Решение геометрическим методом задачи линейного программирования»
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ»
( Н И У « Б е л Г У » )
ИНСТИТУТ ИНЖЕНЕРНЫХ И ЦИФРОВЫХ ТЕХНОЛОГИЙ
КАФЕДРА ПРИКЛАДНОЙ ИНФОРМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Исследование операций и методы оптимизации
Лабораторная работа №3
Тема: Решение геометрическим методом задачи линейного программирования
студентки очного отделения
4 курса, 12001504 группы,
Марко С. Тангуила
Проверил:
Профессор
Черноморец Андрей Алексеевич
Белгород, 2019 год
Цель работы
Получение навыков самостоятельной алгоритмической и программной реализации на компьютерной технике геометрического метода решения задачи линейного программирования в MatLab, научиться строить область допустимых решений задачи линейного программирования, научиться строить линии уровня функции цели, научиться представлять результаты расчетов в виде html-страниц.
Список индивидуальных данных
Решить геометрическим методом задачу линейного программирования, выполнив для этого следующие шаги:
Построить область допустимых решений задачи линейного программирования;
Построить линии уровня функции цели;
Найти точки пересечения линий уровня с границей области допустимых решений;
Создать html-файл «lab4_N.html» с результатами работы, график сохранить в файле с именем «varN», где N – номер варианта;
Подготовить теоретический материал для защиты работы и ответа на контрольные вопросы преподавателя.
Ход Работы
|
| 2x1-5x2 + 10 0, 5x1+8x2 – 40 0, -x1+7x2 + 7 0, x1 0, x2 0, Q = -x1+2x2 min |
Результаты выполнения работы
На первом этапе была построена область допустимых решений – многогранник решений. Для каждого их заданных неравенств на плоскости были построены полуплоскости, то есть множество точек, удовлетворяющих неравенству. Сначала была построена прямая x1=(5x2-10)/2. Эта прямая проходит через точки (0;-5) и (2;0) – точки ее пересечения с осями координат. Затем взяла произвольную точку, не лежащую на этой прямой, например, точку (0;0), и проверила, удовлетворяют ли ее координаты соответствующему неравенству 2x1-5x2 + 10 0. Координаты точки удовлетворяют неравенству, значит вся полуплоскость, в которой находится эта точка, является допустимой (по отношению к этому условию). Таким же образом поступила со всеми неравенствами, заданными в задаче.
В следующей таблице приведены результаты вычисления координат точек, через которые проходят прямые, определяемые неравенствами исходной системы. Получен искомый многогранник решений. На рисунке 1 многогранник решений изображен в виде заштрихованной области.
| Уравнение | X1 | X2 | X1 | X2 | Точка (0;0) |
| 1 | 0 | -5 | 2 | 0 | Удовл. |
| 2 | 0 | 8 | 5 | 0 | Удовл. |
| 3 | 0 | 7 | -1 | 0 | Удовл. |
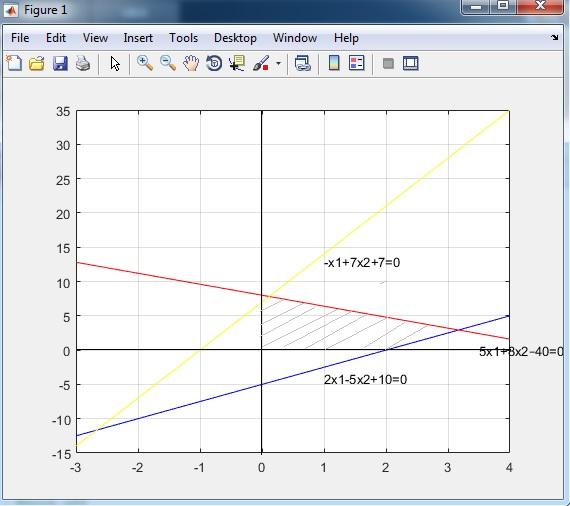
Рисунок 1 – Многогранник решений
На втором этапе были построены прямые – линии уровня целевой функции, то есть линии, во всех точках которых значение целевой функции постоянно. Для этого были выбраны произвольные значения целевой функции, например, Q=-5. Тогда точки, в которых целевая функция принимает значение -5, лежат на прямой – линии уровня Q=-5. (на рисунке эта линия обозначена точками). Все линии уровня, принадлежащие другим значениям, являются прямыми, параллельными прямой Q=-5. Направление, в котором следует параллельно смещать линию уровня, чтобы достичь меньших значений, определим, построив линию уровня Q=0.
В следующей таблице приведены результаты вычисления координат точек, через которые проходят выбранные линии.
| Уравнение | X1 | X2 | X1 | X2 |
| Q=-5 | 0 | 5 | -2.5 | 0 |
| Q=0 | 0 | 0 | 0 | 0 |
Построила линии уровня. Указала с помощью линии со стрелкой, перпендикулярной линии уровня, направление уменьшения значений целевой функции:
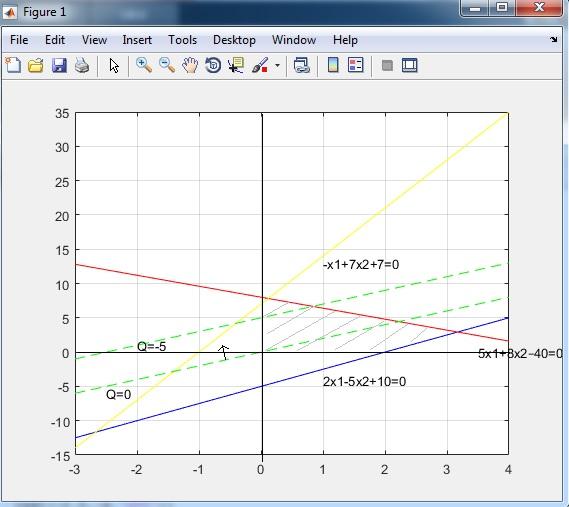
Текст построения графиков в Matlab:
function lab3(x2)
x2=-3:0.5:4;
x1=(5*x2-10)/2;
plot(x2,x1,'b')
text(1,-4,'2x1-5x2+10=0');
hold on
x11=(40-8*x2)/5;
plot(x2,x11,'r')
text(3.5,0,'5x1+8x2–40=0');
hold on
x12=7+7*x2;
plot(x2,x12,'y')
text(1,13,'-x1+7x2+7=0');
hold on
y=2*x2+5;
plot(x2,y,'g--')
text(-2,1,'Q=-5');
hold on
y1=2*x2;
plot(x2,y1,'g--')
text(-2.5,-6,'Q=0');
hold off
grid on;
Путем параллельного переноса линий уровня в направлении меньших значений целевой функции получаем, что множеству P принадлежит одна точка, которая является точкой пересечения прямой, заданной неравенством 3, и неравенством 2.
Для нахождения координат точки P необходимо решить систему уравнений, содержащую уравнения прямых, на пересечении которых лежит точка P.

Решением этой системы является точка х1=0.12, х2=7.8: P = {(0.12;7.8)}.
Текст решения в Matlab:
[x1,x2] = solve('-x1+7*x2+7=0','5*x1+8*x2-40=0')
x1
x2
Решением задачи является точка (0.12;7.8), в которой целевая функция принимает минимальное значение:






















