Тема урока: Математическое моделирование

Тема урока: Математическое моделирование

Тип урока: Изучение нового материала

Задачи урока:

• Ввести понятия «модель задачи», «математическая модель», «вычислительный эксперимент»;

• Рассмотреть этапы решения задач на компьютере;

• Составить алгоритм решения задачи;

• Провести вычислительный эксперимент

Цели урока:

Образовательные:

• Вооружить учащихся знаниями основных понятий по теме;

• Сформировать умение создавать математическую модель;

• Научить проводить вычислительный эксперимент;

• Закрепить навыки решения задач по данной теме

Развивающие:

• Развить у учащихся познавательный интерес, творческие способности, логическое мышление, умения анализировать и делать выводы;

• Расширить мировоззрение и кругозор учащихся

Воспитательные:

• Сформировать у учащихся готовность к информационно – учебной деятельности;

• Воспитать устойчивый интерес к изучению информатики

Средства обучения:

Технические:

• Компьютер с установленной операционной системой Windows

• Мультимедийный проектор

• Экран

Программные:

• Стандартная программа Paint

• Презентация

Раздаточный материал:

• Комплект карточек с задачами

• Комплект карточек с домашним заданием

Мотивация учащихся:

Вспомните себя в детстве. Как вы познавали мир?

С помощью игрушек дети воспринимают окружающий мир. Свою игрушечную машинку ребенок сравнивает с машиной взрослого человека.

Чем является его машинка? (Моделью)

В школе ученики часто используют различные модели на разных уроках. Это скелет человека – на уроке биологии, глобус планеты Земля – на уроке географии и т.д. Оглянитесь вокруг, вспомните, представьте – различные модели, их виды окружают нас повсюду.

Получается, что модели с нами в течение всей нашей жизни.

Сегодня мы познакомимся еще одним видом моделей - математическими моделями.

План урока:

1. Организационный момент

2. Актуализация опорных знаний

3. Объяснение нового материала

4. Закрепление полученных знаний

5. Подведение итогов урока

6. Домашнее задание

Ход урока:

I. Организационный момент

Учитель объявляет тему и цели урока. На экране представлена презентация урока.

II. Актуализация опорных знаний

Тестирование

1. Модель – это …

а) визуальный объект;

б) свойство процесса или явления;

в) упрощенное представление о реальном объекте, процессе или явлении;

г) материальный объект

2. Моделирование, при котором реальному объекту ставится в соответствие его увеличенная или уменьшенная копия, называется …

а) идеальным;

б) формальным;

в) материальным;

г) математическим

3. Моделирование, при котором исследование объекта осуществляется посредством модели, сформированной на языке математики, называется …

а) арифметическим;

б) аналоговым;

в) математическим;

г) знаковым

4. Моделирование, основанное на мысленной аналогии, называется …

а) мысленным;

б) идеальным;

в) знаковым;

г) физическим

5. Какая из моделей не является знаковой?

а) схема;

б) музыкальная тема;

в) график;

г) рисунок

6. Детская игрушка – это …

а) знаковая модель;

б) вербальная модель;

в) материальная модель;

г) компьютерная модель

7. Динамическая модель – это …

а) одномоментный срез объекта;

б) изменение объекта во времени;

в) интегральная схема;

г) детская игрушка

8. Компьютерная модель – это …

а) информационная модель, выраженная специальными знаками;

б) комбинация нулей и единиц;

в) модель, реализованная средствами программной среды;

г) физическая модель

9. Вербальная модель – это …

а) компьютерная модель;

б) информационная модель в мысленной или разговорной форме;

в) информационная модель, выраженная специальными знаками;

г) материальная модель

10. Что является моделью объекта яблоко?

а) муляж;

б) фрукт;

в) варенье;

г) компот

III. Объяснение нового материала

Математическое моделирование

Математическое моделирование – это идеальное научное знаковое формальное моделирование, при котором описание объекта осуществляется на языке математики, а исследование модели проводится с использованием тех или иных математических методов.

Математическое моделирование широко применяется в естественных науках. Например, практически все современные разделы физики (механика, теория тепломассообмена, электротехника и др.) посвящены построению и исследованию математических моделей различных физических объектов и явлений. Математизация конкретных технических дисциплин позволяет:

1) единообразно описывать (формализовать) широкий круг фактов и наблюдений;

2) проводить количественный анализ (исследовать);

3) предсказывать поведение системы в различных условиях (прогнозировать).

В зависимости от целей математического моделирования выделяют дескриптивные, оптимизационные и управленческие модели.

Целью дескриптивных моделей является установление законов изменения параметров модели, например, в виде уравнения.

Оптимизационные модели предназначены для определения оптимальных (наилучших) с точки зрения некоторого критерия (стоимости, надежности, производительности, жесткости и др.) параметров моделируемого объекта или же для поиска оптимального режима управления некоторым процессом.

Управленческие модели применяются для принятия эффективных управленческих решений в различных областях целенаправленной деятельности человека. На практике под принятием решений обычно понимается выбор некоторых альтернатив из заданного их множества, а общий процесс принятия решений представляется как последовательность таких выборов альтернатив.

В современных исследованиях и проектах в области машиностроения математическое моделирование служит для изучения производственных систем (производственных объектов, процессов и явлений), поддержки научных разработок, обеспечения процедур автоматизированного проектирования и т.д.

Следует отметить основные преимущества математического моделирования по сравнению с натурными исследованиями:

- значительно меньшая материало- и энергоемкость (сбережение ресурсов);

- возможность исследования гипотетических (не реализованных в природе) объектов;

- возможность исследования критических режимов функционирования объекта (опасных, трудновоспроизводимых или чреватых разрушением дорогостоящей техники);

- возможность изменения хода (масштаба) времени;

- сокращение сроков на подготовку и анализ данных;

- возможность многоаспектного анализа, изучение объектов в достаточной полноте;

- возможность выявления общих закономерностей и составления прогнозов;

- использование результатов в работе специального технического и программного обеспечения.

«Чистая» и прикладная математика предлагает различные определения математической модели. С точки зрения «чистой» математики математическая модель – это множество абстрактных, символьных математических объектов (таких как числа, переменные, векторы, матрицы, множества, точки, отрезки, прямые и т.д.) и отношений между ними (правил, связывающих два и более символьных объекта).

Для «чистой» математики характерен больший формализм, оперирование абстрактными понятиями, что, с одной стороны, можно считать недостатком, а с другой – положительным качеством, повышающим общность определения модели, делающим ее применимой к объектам различной природы.

Для прикладной математики характерна меньшая оторванность от реальности, поскольку математические соотношения связывают не просто абстрактные математические объекты, а вполне конкретные параметры объектов реальных. С точки зрения прикладной математики математическая модель – это некоторый оператор  , позволяющий по соответствующим значениям входных параметров 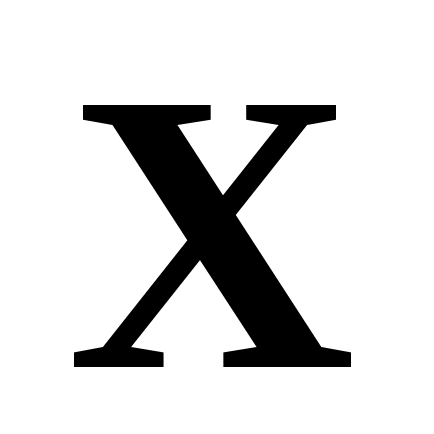  установить значения выходных параметров  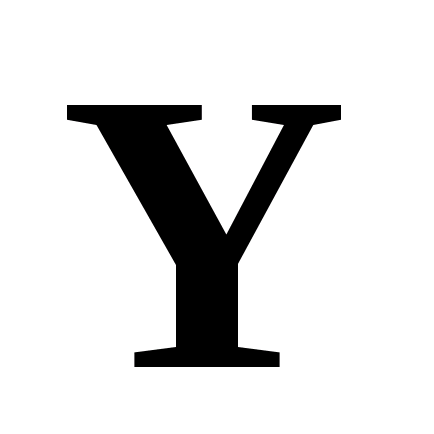 объекта моделирования:

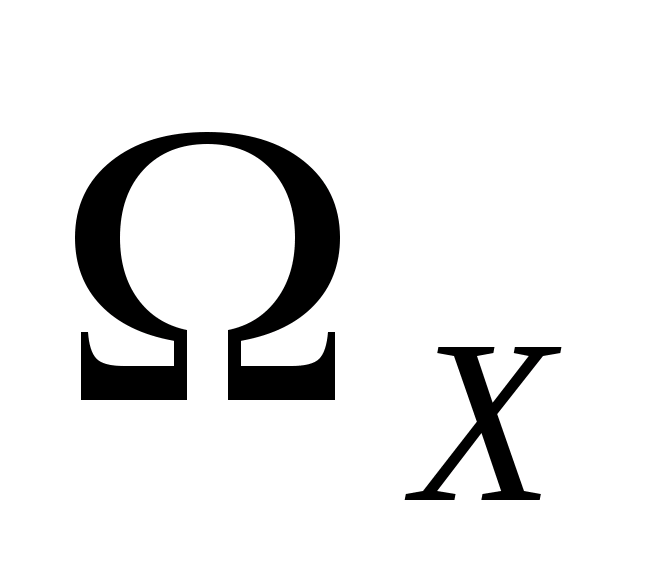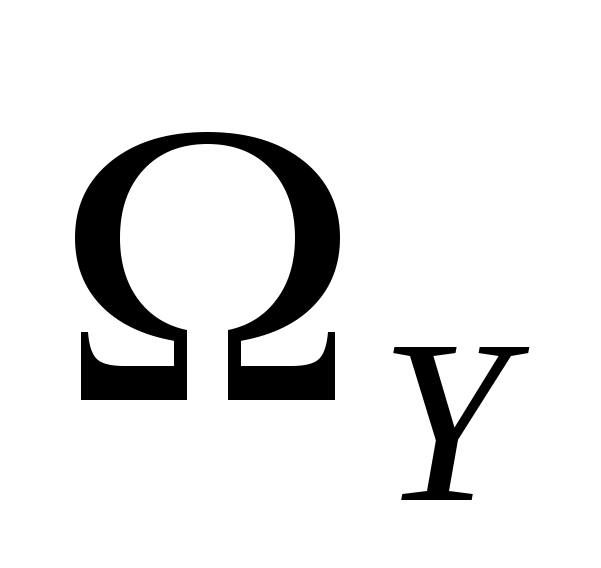где   и   – соответственно множества допустимых значений входных и выходных параметров, элементами которых могут быть любые математические объекты (числа, матрицы, функции, множества и т.д.), в зависимости от природы исследуемого объекта.

Понятие оператора также может трактоваться достаточно широко. Это может быть некоторая функция, схема, алгоритм, система уравнений, совокупность правил и другое, т.е. то, что обеспечивает нахождение выходных параметров по заданным исходным значениям входных параметров.

Вид, состав и сложность конкретной математической модели зависит от того, какой объект она описывает и для каких целей разработана. Однако построение математических моделей многих элементов технических систем упрощается благодаря использованию типовых моделей [3-5]. Например, при описании геометрии объекта можно воспользоваться уравнениями линий и поверхностей. В то же время существуют задачи, требующие изучения закономерностей процессов и явлений, связанных с моделируемым объектом, выделения существенных факторов, принятия различного рода допущений и их обоснования, математической интерпретации имеющихся сведений и т.п. Построение математической модели в этом случае является творческим процессом и требует специальной подготовки как в соответствующих предметных областях, так и в вопросах математики.

Существует большое число классификаций математических моделей, однако, учитывая большое число возможных классификационных признаков и субъективность их выбора, каждую из них следует считать условной.