СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока


Тема урока: Повторение материала по темам. «Обыкновенные дроби» и «Смешанные дроби»
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: 01.49.1.Пчеловод
Преподаватель:
Тема урока: Повторение материала по темам. «Обыкновенные дроби» и «Смешанные дроби»
Перечень рассматриваемых вопросов:
- Повторение понятий обыкновенных и смешанных дробей.
- Перевод из неправильной дроби в смешанную и обратно.
- Действия с дробями.
- Практическое применение дробей.

Сумма (разность) дробей с общим знаменателем есть дробь, числитель которой равен сумме (разности) числителей, а знаменатель равен знаменателю данных дробей.
Если числитель и знаменатель дроби умножить (разделить) на одно и то же натуральное число, то получится равная ей дробь.
Дробь называется правильной, если её числитель меньше знаменателя.
Дробь называется неправильной, если её числитель больше знаменателя или равен ему.
Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Чтобы умножить натуральное число на дробь, можно числитель дроби умножить на это число, а знаменатель оставить тот же.
Чтобы разделить дробь на дробь, можно делимое умножить на дробь, обратную делителю.
Чтобы разделить дробь на натуральное число, можно её знаменатель умножить на это число.
Теоретический материал для самостоятельного изучения
Дробь.



Любое натуральное число можно представить в виде дроби:

Сложение и вычитание дробей с одинаковыми знаменателями.
Сумма (разность) дробей с общим знаменателем есть дробь, числитель которой равен сумме (разности) числителей, а знаменатель равен знаменателю данных дробей.

Основное свойство дроби.
Если числитель и знаменатель дроби умножить (разделить) на одно и то же натуральное число, то получится равная ей дробь.


Правильные и неправильные дроби.
Дробь называется правильной, если её числитель меньше знаменателя.

- Найдем наименьший общий знаменатель, то есть найдём НОК (5,7) = 35
- Разделим наименьший общий знаменатель на знаменатель каждой дроби, то есть найдём дополнительный множитель

Умножим числитель и знаменатель каждой дроби на дополнительный множитель:

Сложение и вычитание дробей с разными знаменателями.
Чтобы сложить (вычесть) две дроби с разными знаменателями, их надо привести к общему знаменателю, а затем применить правило сложения (вычитания) дробей с общим знаменателем.

Умножение и деление дробей.
Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.

Чтобы умножить натуральное число на дробь, можно числитель дроби умножить на это число, а знаменатель оставить тот же.

Частное любых двух натуральных чисел равно дроби, числитель которой равен делимому, а знаменатель – делителю.

Смешанные дроби.
Неправильную дробь можно представить в виде смешанной дроби.

Действия со смешанными дробями.
Чтобы сложить (вычесть) две смешанные дроби, надо сложить (вычесть) отдельно их целые и их дробные части и полученные результаты сложить.

Чтобы умножить или разделить смешанные дроби, можно записать их в виде неправильных дробей и выполнить действия с обыкновенными дробями.

Задача.
Муж выпьет кадь воды за 5 дней, а с женой выпьет ту же кадь за 4 дня. Спрашивается, за сколько дней жена его отдельно выпьет ту же кадь.
Решение. Примем объём кади за единицу.

Разбор заданий тренировочного модуля
№ 1. Единичный выбор.

№ 2. Выделение цветом.
Просмотр содержимого документа
«Тема урока: Повторение материала по темам. «Обыкновенные дроби» и «Смешанные дроби»»
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: 01.49.1 Пчеловод
Преподаватель:
Тема урока: Множества чисел. Арифметические действия над ними.
Основная теорема арифметики гласит, что любое составное натуральное число однозначно разлагается в произведение простых чисел.
Пример 1: разложить число 18 на простые числа.
Решение: 18 = 2·3·3,
18 – это произведение 2·3·3 = 2·32.
Значит, составное число однозначно разложилось в произведение простых множителей.
Пример 2: разложить число 12 на простые числа.
Решение:12 = 2·2·3.
12 = 22·3.
Наибольший общий делитель
Рассмотрим понятия ![]() и
и ![]() чисел.
чисел.
НОД – наибольший общий делитель двух чисел. НОД двух целых чисел ![]() и
и ![]() , одновременно не равных нулю, называется такое наибольшее целое число
, одновременно не равных нулю, называется такое наибольшее целое число ![]() , на которое
, на которое ![]() и
и ![]() делятся без остатка. Этот факт обозначается так:
делятся без остатка. Этот факт обозначается так:![]() . Если оба числа равны нулю, то положим
. Если оба числа равны нулю, то положим ![]() .
.
Пример 3: Найти ![]()
Решение: Разложим 12 и 18 на простые числа.
![]()
![]()
Необходимо определить общие делители 18 и 12 (из простых чисел), их произведение будет ![]() .
.
![]() .
.
Ответ: 6
Наименьшее общее кратное
НОК – наименьшее общее кратное двух чисел. НОК двух целых чисел ![]() и
и ![]() называется наименьшее положительное целое число, кратное как
называется наименьшее положительное целое число, кратное как ![]() , так и
, так и ![]() .
.
Пример 4: найти ![]() .
.
Решение: Используем основную теорему арифметики для решения данной задачи.
Разложим 20 и 30 на простые множители.
![]()
![]() .
.
Общие делители: 20 и 30: 2 и 5
![]()
Ответ: 60.
Пример использования НОК
Для того, чтобы понять, где применяются НОД и НОК рассмотрим следующий пример.
Пример 5. Найти значение ![]() .
.
Решение: Для того, чтобы привести дробь к общему знаменателю необходимо найти ![]() .
.
![]() .
.
Значит, ![]()
Найдем дополнительные множители.
Дополнительный множитель ![]() = 36 : 12= 3;
= 36 : 12= 3;
Дополнительный множитель ![]() = 36 : 18= 2;
= 36 : 18= 2;
Значит, ![]() .
.
Ответ: ![]() .
.
Пример использования НОД
Пример 6: Найти значений ![]()
Решение: Основное свойство дроби заключается в том, что числитель и знаменатель можно разделить или умножить на одно и то же число. Найдем это число из разложения по основной теореме арифметики.
![]() .
.
Числитель и знаменатель можно сократить на 2 и на 3.
![]() .
.
Ответ: ![]()
Примеры решения задачи 1 на НОК и НОД
Пример 7. Решите задачу.
В классе каждый человек получил по подарку. Подарки состояли из апельсинов и яблок. Для подарков закупили 123 апельсина и 82 яблока. Каждому ученику в классе раздали одинаковый подарок и потратили все апельсины и все яблоки.
Вопрос 1: сколько учеников в классе? Вопрос 2: Сколько в каждом подарке было апельсинов, сколько в каждом подарке было яблок?
Решение.
Разложим 123 на произведение простых множителей.
123 = 3·41.
Точно так же поступим с числом яблок.
82 = 2·41.
Необходимо найти число учеников в классе и из чего состоит каждый подарок.
Найдем ![]() .
.
![]() .
.
Значит, в классе учится 41 ученик.
Найдем, из чего состоял каждый подарок.
Количество апельсинов: ![]()
Количество яблок: ![]()
Ответ: 1. В классе учится 41 ученик. 2. В каждом подарке было 3 апельсина и 2 яблока.
Примеры решения задачи 2 на НОК и НОД
Пример 8. Решите задачу.
Шаг Володи 75 см., а шаг Кати 60 см. Первый шаг они сделали в ногу, а потом у них разное число шагов. На какой расстоянии они сделают следующий шаг в ногу?
На каком наименьшем расстоянии они сделают по целому числу шагов?
Решение: Найдем ![]() .
.
Чтобы найти наименьшее общее кратное двух чисел, мы, согласно основной теореме арифметики, раскладываем эти числа на простые множители.
75 = 3·5·5;
60 = 2·2·3·5;
![]() .
.
Ответ на вопрос: 300 см.
Найдем количество шагов, которое сделает каждый на данном расстоянии.
Володя сделает = ![]() = 4 шага.
= 4 шага.
Катя 300 сделает = ![]() = 5 шагов.
= 5 шагов.
Ответ: Катя и Володя следующий шаг сделают на расстоянии 300 см, для этого Володя сделает 4 шага, а Катя – 5 шагов.
Итак, мы рассмотрели основные числовые множества. Именно из этих множеств буквенные переменные принимают свои числовые значения. Мы вспомнили, что такое натуральные числа, что такое целые числа, что такое дробные числа. Основное внимание мы уделили натуральным числам. В натуральных числах мы вспомнили, что такое простые множители. Это те множители, которые делятся только на себя и на единицу. И вспомнили основную теорему арифметики, согласно которой каждое составное число однозначно раскладывается в произведение простых множителей. Вспомнили важные понятия НОД и НОК и типовые задачи на них.
На следующем уроке мы повторим числовые выражения и действия с дробными числами.
Список рекомендованной литературы
Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
Образовательная компания МастерВУЗ (Источник).
Studlab.com - Студенческая лаборатория (Источник).
Рекомендованное домашнее задание
1. Найдите НОК следующих чисел:
НОК(3,12) = НОК(9;15) =
НОК(4;5;8)= НОК(12;10)=
НОК(8;12)= НОК(9;6) =
НОК(16;12)= НОК(10;20)=
2. Найдите НОД и НОК чисел наиболее удобным способом .
а) 12 и 18; г) 10 и 15;
б) 13 и 39; д) 19 и 57;
в) 11 и 15; е) 7 и 12.
3. Из речного порта одновременно 1 марта 2013 года вышли два теплохода. Продолжительность рейса одного из них – 15 суток, а продолжительность рейса второго – 24 суток. Через сколько дней теплоходы снова одновременно отправятся в рейс? Сколько рейсов за это время сделает первый теплоход ? А сколько второй?
4. Найти числа а и b, если известно, что НОK(a, b) = 105, a·b = 525.
Найти числа а и b, если известно, что НОД(a, b) = 7, a·b = 294.
Найти числа а и b, если известно, что НОД(a, b) = 5, a:b = 13:8.
Найти числа а и b, если известно, что НОK(a, b) = 224, a:b = 7:8.
Найти числа a и b, если известно, что НОД(a, b) = 3, НОK(a; b) = 915.
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: 01.49.1.Пчеловод
Преподаватель:
Тема урока: Повторение материала по темам. «Обыкновенные дроби» и «Смешанные дроби»
Перечень рассматриваемых вопросов:
Повторение понятий обыкновенных и смешанных дробей.
Перевод из неправильной дроби в смешанную и обратно.
Действия с дробями.
Практическое применение дробей.

Сумма (разность) дробей с общим знаменателем есть дробь, числитель которой равен сумме (разности) числителей, а знаменатель равен знаменателю данных дробей.
Если числитель и знаменатель дроби умножить (разделить) на одно и то же натуральное число, то получится равная ей дробь.
Дробь называется правильной, если её числитель меньше знаменателя.
Дробь называется неправильной, если её числитель больше знаменателя или равен ему.
Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Чтобы умножить натуральное число на дробь, можно числитель дроби умножить на это число, а знаменатель оставить тот же.
Чтобы разделить дробь на дробь, можно делимое умножить на дробь, обратную делителю.
Чтобы разделить дробь на натуральное число, можно её знаменатель умножить на это число.
Теоретический материал для самостоятельного изучения
Дробь.


Любое натуральное число можно представить в виде дроби:

Сложение и вычитание дробей с одинаковыми знаменателями.
Сумма (разность) дробей с общим знаменателем есть дробь, числитель которой равен сумме (разности) числителей, а знаменатель равен знаменателю данных дробей.
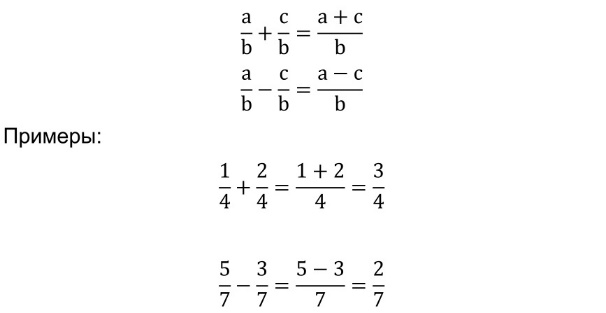
Основное свойство дроби.
Если числитель и знаменатель дроби умножить (разделить) на одно и то же натуральное число, то получится равная ей дробь.
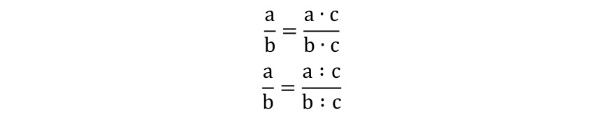

Правильные и неправильные дроби.
Дробь называется правильной, если её числитель меньше знаменателя.

Найдем наименьший общий знаменатель, то есть найдём НОК (5,7) = 35
Разделим наименьший общий знаменатель на знаменатель каждой дроби, то есть найдём дополнительный множитель

Умножим числитель и знаменатель каждой дроби на дополнительный множитель:

Сложение и вычитание дробей с разными знаменателями.
Чтобы сложить (вычесть) две дроби с разными знаменателями, их надо привести к общему знаменателю, а затем применить правило сложения (вычитания) дробей с общим знаменателем.

Умножение и деление дробей.
Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.

Чтобы умножить натуральное число на дробь, можно числитель дроби умножить на это число, а знаменатель оставить тот же.
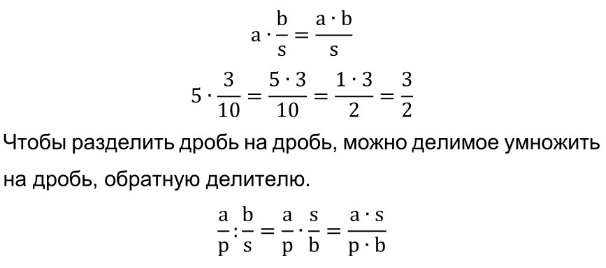
Частное любых двух натуральных чисел равно дроби, числитель которой равен делимому, а знаменатель – делителю.

Смешанные дроби.
Неправильную дробь можно представить в виде смешанной дроби.

Действия со смешанными дробями.
Чтобы сложить (вычесть) две смешанные дроби, надо сложить (вычесть) отдельно их целые и их дробные части и полученные результаты сложить.
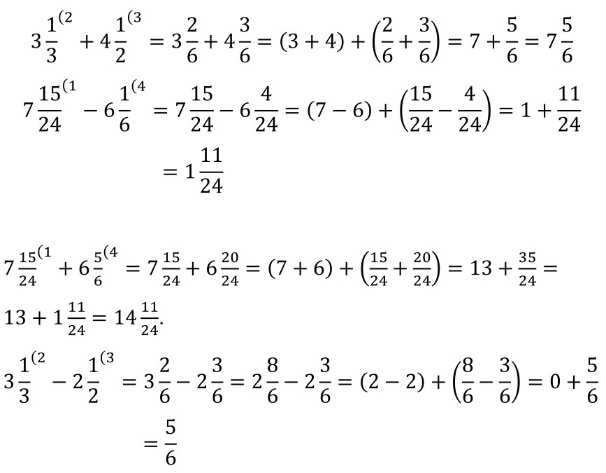
Чтобы умножить или разделить смешанные дроби, можно записать их в виде неправильных дробей и выполнить действия с обыкновенными дробями.

Задача.
Муж выпьет кадь воды за 5 дней, а с женой выпьет ту же кадь за 4 дня. Спрашивается, за сколько дней жена его отдельно выпьет ту же кадь.
Решение. Примем объём кади за единицу.

Разбор заданий тренировочного модуля
№ 1. Единичный выбор.
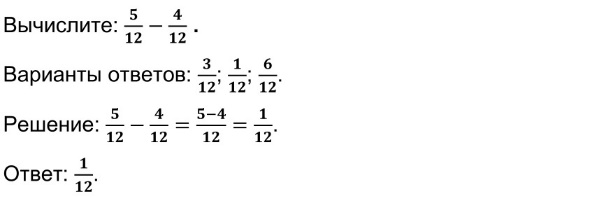
№ 2. Выделение цветом.

План урока
Курс__, гр__
Дисциплина: Математика
Профессия: 01.49.1. Пчеловод
Преподаватель:
Тема урока: Решение линейных уравнений с одним неизвестным
Перечень рассматриваемых вопросов:
• Линейные уравнения.
• Корень уравнения.
• Решение линейных уравнений.
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.
Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.
Свободный член – член уравнения, не содержащий неизвестного.
Решить уравнение – значит найти все его корни или установить, что их нет.
Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.

Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Теоретический материал для самостоятельного изучения.
 Давайте вспомним, что называется корнем уравнения?
Давайте вспомним, что называется корнем уравнения?
Корнем уравнения называют, такое значение переменной, при которой уравнение преобразуется в верное числовое равенство.
А что же означает решить уравнение?
Решить уравнение означает найти все его корни или доказать, что корней нет.
Давайте попробуем сформулировать теперь, как решать линейные уравнения и подумаем, а какие у нас могут быть случаи?
Решение линейного уравнения – это приведение его путем тождественных преобразований к стандартному виду.
Давайте решим уравнение:
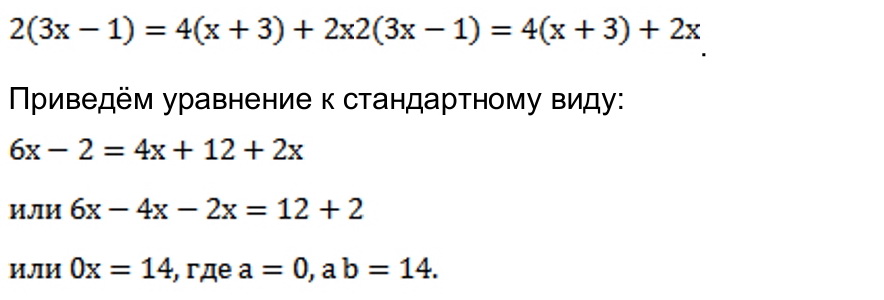
Следовательно, уравнение не имеет корней.
А теперь давайте решим другое уравнение:

Попробуем решить уравнение:
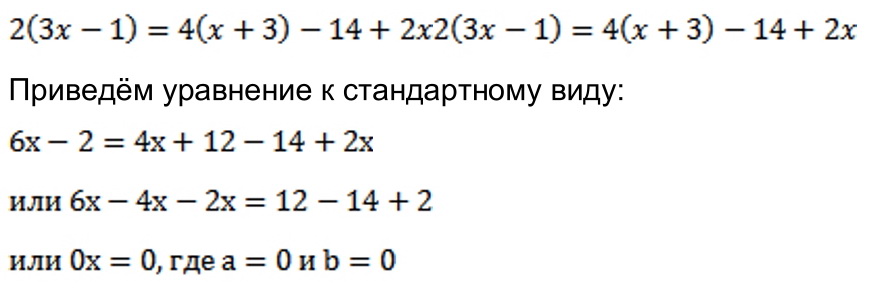
При любом значении переменной, уравнение принимает вид верного равенства:
0 = 0, следовательно, уравнение имеет бесконечное множество корней.
Отсюда можно сделать вывод, что возможные варианты решения уравнения, зависят от того, какие значения принимает свободный член и коэффициент при переменной.
При решении уравнения вида возможны следующие три случая:
 Замечательно, а теперь узнаем, можно ли проверить, является число корнем уравнения не решая его?
Замечательно, а теперь узнаем, можно ли проверить, является число корнем уравнения не решая его?
Да, конечно можно. Для этого нужно подставить в уравнение вместо переменной это число, если после упрощения, мы получаем верное равенство, то данное число будет являться корнем уравнения.
Давайте проверим, так ли это. Узнаем, является ли число

Замечательно. А теперь давайте попробуем порешать линейные уравнения первой степени.
 является корнем уравнения.
является корнем уравнения.
 уравнение к стандартному виду. Слагаемые, зависящие от икс, перенесём в левую часть уравнения, числа – в правую, изменяя их знаки на противоположные.
уравнение к стандартному виду. Слагаемые, зависящие от икс, перенесём в левую часть уравнения, числа – в правую, изменяя их знаки на противоположные.
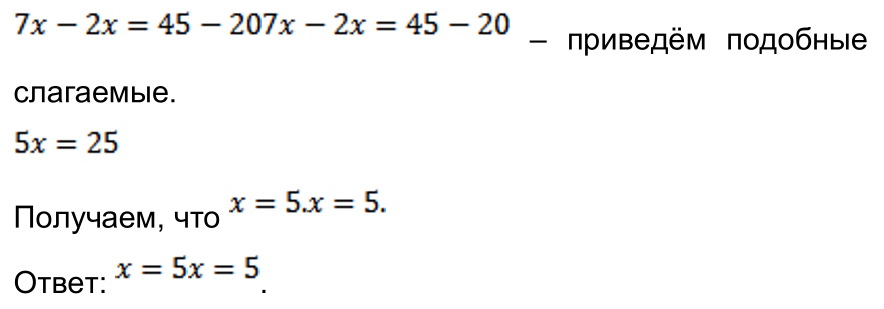
Разбор заданий тренировочного модуля.
 содержащие переменной в правую часть, меняя знак на противоположный;
содержащие переменной в правую часть, меняя знак на противоположный;

 слагаемые, содержащие переменную в левую часть, не содержащие переменной, в правую часть, меняя знак на противоположный;
слагаемые, содержащие переменную в левую часть, не содержащие переменной, в правую часть, меняя знак на противоположный;

План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Квадратные уравнения. Неполные квадратные уравнения.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Если D
Если D = 0, есть ровно один корень;
Если D 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
x2 − 8x + 12 = 0;
5x2 + 3x + 7 = 0;
x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D 0, корни можно найти по формулам:
![]() Основная формула корней квадратного уравнения
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
Задача. Решить квадратные уравнения:
x2 − 2x − 3 = 0;
15 − 2x − x2 = 0;
x2 + 12x + 36 = 0.
Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.
D 0 ⇒ уравнение имеет два корня. Найдем их:
![]()
Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.
D 0 ⇒ уравнение снова имеет два корня. Найдем их
Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
x2 + 9x = 0;
x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
![]() Решение неполного квадратного уравнения
Решение неполного квадратного уравнения
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
Если же (−c/a)
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
![]() Вынесение общего множителя за скобку
Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
x2 − 7x = 0;
5x2 + 30 = 0;
4x2 − 9 = 0.
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Соотношение между градусной и радианной мерами угла.
Соотношение между градусной и радианной мерами угла
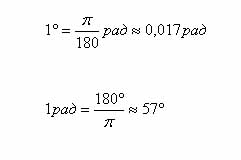 Определения:
Определения:
Тригонометрические функции острых углов можно определить как отношение длин сторон прямоугольного треугольника.
Синус:
![]()
Косинус:
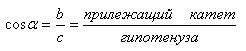
Тангенс:
![]()
Котангенс:
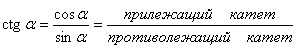
Синус и косинус угла определены для любого угла α. Тангенс определен для всех значений угла α, кроме α = π/2 + πn (a = 90º + 180º * n), n = 0, +/- 1, +/- 2,... . Котангенс определен для всех значений угла α, кроме α = πn (α = 180º * n), n = 0, +/- 1, +/- 2, ...
Функции sin α , cos α, sec α и cosec α имеют период 2π, а функции tg α и ctg α - период π:
sin(α + 2πn) = sin α; cosec(α + 2πn) = cosec α;
cos(α + 2πn) = cos α; sec α + 2πn) = sec α;
tg (α + πn) = tgα;
ctg (α + πn) = ctg α; n = 0, +/- 1, +/- 2,... .
Формулы приведения
Вычисление значений тригонометрических функций любого угла сводится к вычислению значений тригонометрических функций острого угла по следующим правилам:

Самостоятельная работа
Упростить выражение:
1) ![]() ;
;
2) ![]() .
.
3)![]() ;
;
4) ![]() .
.
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Свойства функции: монотонность, чётность, нечётность, ограниченность, периодичность
Функция - это одно из важнейших математических понятий. Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по оси ординат откладываются значения переменной y. Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!
Для построения графика функции советуем использовать нашу программу - Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции - это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции.
Значения х, при которых y=0, называется нулями функции. Это абсциссы точек пересечения графика функции с осью Ох.

3) Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие промежутки значений x, на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.

4) Монотонность функции.
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
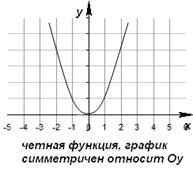
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого хиз области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
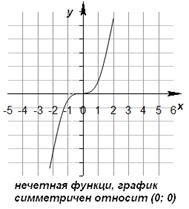
Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
Четная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.

6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.
7) Периодическость функции.
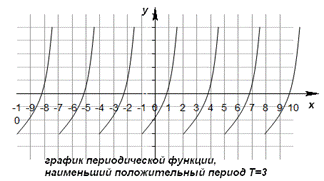
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Функция f называется периодической, если существует такое число , что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T). T - это период функции.
Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.
Задание №1. Изобразите схематически график и опишите свойства функции: y = x2 .
Контрольные вопросы:
1. Что называется функцией?
2. Что такое область определения функции?
3. Какая функция называется четной, нечетной?
4. Как найти область значения функции и привести пример?
5. Оформить отчет о проделанной работе.
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока:Тесты. Тригонометрические функции
А. Выберите правильный ответ.
A1. Найдите область определения функции у = 2sin x + tg x.
1) х – любое число; 2) х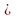 R, кроме х=0; 3) х
R, кроме х=0; 3) х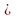 R, кроме
R, кроме 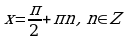 ;
;
4) х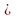 R, кроме х=1.
R, кроме х=1.
А2. Какими свойствами обладает функция у = 2 – sin 3x ?
1) нечетная, периодическая; 2) ни четная ни нечетная, непериодическая;
3) четная, периодическая; 4) ни четная ни нечетная, периодическая.
А3. Найдите все корни уравнения tg x = 1, принадлежащие промежутку [-; 2].
1)  ;
; 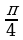 ;
; 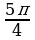 ; 2)
; 2) 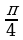 ;
; 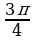 ;
; 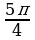 ; 3)
; 3) 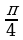 ;
; 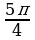 ; 4)
; 4) 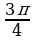 ;
; 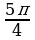 ;
;  .
.
А4. Найдите наименьший положительный период функции у = 2sin 3x.
1) ; 2) 3; 3)  ; 4)
; 4) 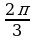 .
.
А5. Выберите верное неравенство:
1) tg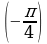
 ; 2) tg
; 2) tg 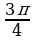
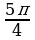 ; 3) tg
; 3) tg  tg
tg 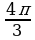 ; 4) tg
; 4) tg 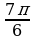
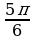 .
.
B. Запишите правильный ответ.
В1. Найдите длину отрезка, который является областью значений функции
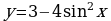
В2. Найдите сумму всех корней уравнения 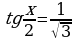 , принадлежащие промежутку
, принадлежащие промежутку 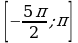 .
.
В3.Сколько целых чисел из промежутка 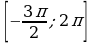 принадлежит области определения функции
принадлежит области определения функции 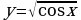 ?
?
С. Для каждого задания приведите решение и укажите ответ.
С1. Найдите все значения х, при которых функция у = 1 – 2cos2 x принимает положительные значения.
С2. Найдите множество значений функции у = 2sin x , если х принадлежит промежутку  .
.
С3. Постройте график функции у = |cos x|.
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Преобразование тригонометрических выражений.
Преобразование тригонометрических выражений – это упрощение выражений, которое выполняется с помощью тригонометрических формул.
Теоретический материал для самостоятельного изучения
Преобразование тригонометрических выражений – это их упрощение, которое выполняется с помощью тригонометрических формул.
Вот некоторые правила, которые помогут нам преобразовывать тригонометрические выражения.
Если в тригонометрических выражениях разные меры угла, то их следует привести к единой, применяя правила:
1)![]() )
)![]()
Например: ![]()
2)![]()
Например: ![]() .
.
Если синусы, косинусы, тангенсы и котангенсы содержат разные аргументы, (углы),стараемся привести к одному аргументу (углу).
Например, с помощью формул двойного аргумента(угла) ![]() заменяем на
заменяем на ![]() по формуле
по формуле ![]() .
.
Если в тригонометрическом выражении необходимо поменять синус на косинус, тангенс на котангенс, то применяем формулы приведения.
Например: ![]() , так как
, так как ![]() , синус меняется на косинус.
, синус меняется на косинус.
![]() , так как
, так как ![]() , тангенс меняется на котангенс, угол в четвёртой четверти, здесь тангенс отрицательный.
, тангенс меняется на котангенс, угол в четвёртой четверти, здесь тангенс отрицательный.
Если тригонометрические выражения содержат большое количество тригонометрических функций, то необходимо привести к минимальному количеству видов функций. Для этого используем формулы приведения, основное тригонометрическое тождество или другие формулы.
Например:
вычислить ![]() .
.
Заметим, что ![]() ,
, ![]() ,
, ![]() .
.
Тогда данное выражение примет вид: ![]() ;
;
в скобках формула косинуса двойного угла, т.е. ![]() , значит
, значит
![]()
Если в тригонометрическом выражении нужно понизить степень входящих в него компонентов, применяем формулу понижения степени или формулу половинного аргумента. Только помните: степень понижается, аргумент удваивается.
![]() ,
,![]() ,
, ![]() ,
, ![]()
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.
Например: упростите выражение ![]() .
.
Применяем формулу понижения степени для косинуса и получаем:
![]() .
.
Чтобы определить рациональность значения тригонометрического выражения, мы должны знать, что из всех углов, содержащих рациональное число, лишь углы вида ![]() ;
; ![]() ;
; ![]() , где k целое число, имеют рациональный косинус.
, где k целое число, имеют рациональный косинус.
Например, ![]() число рациональное, так как
число рациональное, так как ![]() .
.
Углы вида ![]() ;
; ![]() ;
; ![]() , где k целое число, имеют рациональный синус.
, где k целое число, имеют рациональный синус.
Углы вида ![]() ;
; ![]() , где k целое число, имеют рациональный тангенс.
, где k целое число, имеют рациональный тангенс.
Примеры и разбор решения заданий тренировочного модуля:
Рассмотрим примеры преобразований тригонометрических выражений.
Пример 1.Вычислите: ![]() .
.
Заметим, что в знаменателе данной дроби у синусов разные углы ![]() и
и ![]() . Используем формулу приведения:
. Используем формулу приведения: ![]() и тогда наше выражение примет вид:
и тогда наше выражение примет вид: ![]() , в знаменателе тригонометрическое тождество, равное 1. Нам осталось 24 разделить на 1, получаем 24.
, в знаменателе тригонометрическое тождество, равное 1. Нам осталось 24 разделить на 1, получаем 24.
Пример 2. Найдите ![]() , если
, если ![]() .
.
Так как ![]() , то разделив числитель и знаменатель данной дроби на
, то разделив числитель и знаменатель данной дроби на ![]() . Получаем:
. Получаем:
 , сократим и заменим
, сократим и заменим ![]() на
на![]() .
.
![]() , по условию
, по условию ![]() =3, подставим это число в наше выражение:
=3, подставим это число в наше выражение: ![]() .
.
Самостоятельно.
Доказать тождество: ![]()
Упростить выражение: ![]()
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
ТЕМА УРОКА:РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Простейшими тригонометрическими уравнениями называют уравнения
cos x = a, sin x = a, tg x = a, ctg x = a.
Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.
19.1. Уравнение cos x = a
Таблица 1

Объяснение и обоснование
Корни уравнения cos x = a.
При |a| 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a 1 или при a y = cos x).
Пусть | a | ≤ 1. Тогда прямая y = a пересекает график функции y = cos x (рис. из пункта 1 табл. 1). На промежутке [0; π] функция y = cos x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = a имеет на этом промежутке только один корень, который по определению арккосинуса равен: x1 = arccos a (и для этого корня cos x = a).
Косинус – четная функция, поэтому на промежутке [-π; 0] уравнение cos x = a также имеет только один корень – число, противоположное x1, то есть x2 = - arccos a.
Таким образом, на промежутке [-π; π] (длиной 2π) уравнение cos x = a при |a| ≤ 1 имеет только корни x = ±arccos a.
Функция y = cos x периодическая с периодом 2π, поэтому все остальные корни отличаются от найденных на 2πn (n ∈ Z). Получаем следующую формулу корней уравнения cos x = a при |a| ≤ 1:
x = ±arccos a + 2πn, n ∈ Z (1)
Частые случаи решения уравнения cos x = a.
Полезно помнить специальные записи корней уравнения cos x = a при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность.
Поскольку косинус равен абсциссе соответствующей точки единичной окружности, получаем, что cos x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка А или точка В (рис. из пункта 2 табл. 1). Тогда

Аналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка С, следовательно, x = 2πk, k ∈ Z.
Также cos x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка D, таким образом, x = п + 2πk, k ∈ Z
Примеры решения задач




19.2. Уравнение sin x = a
Таблица 2
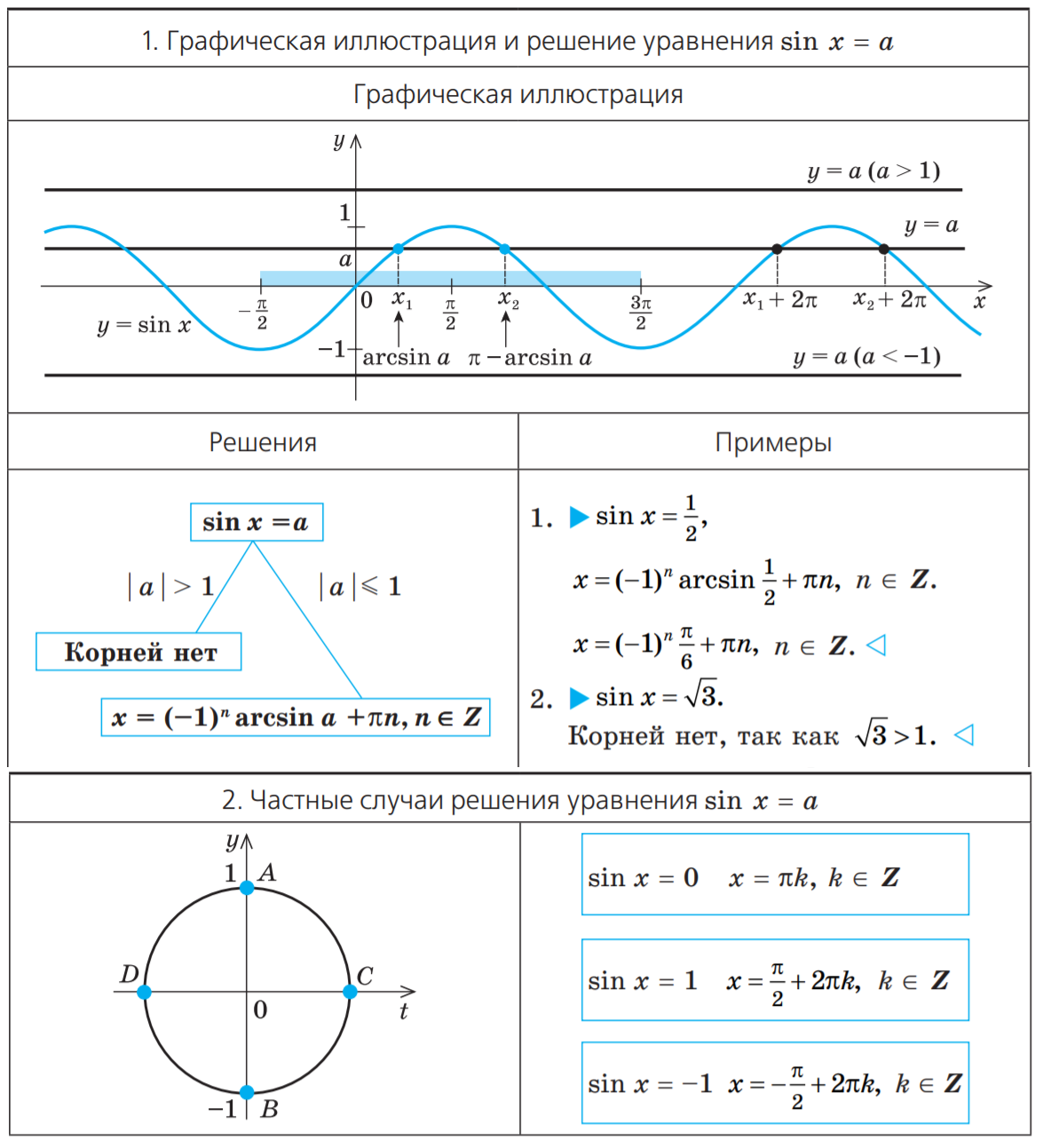
Объяснение и обоснование
1.Корни уравнения sin x = a.
При |a| 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a 1 или при a y = sin x).
Рисунок 1
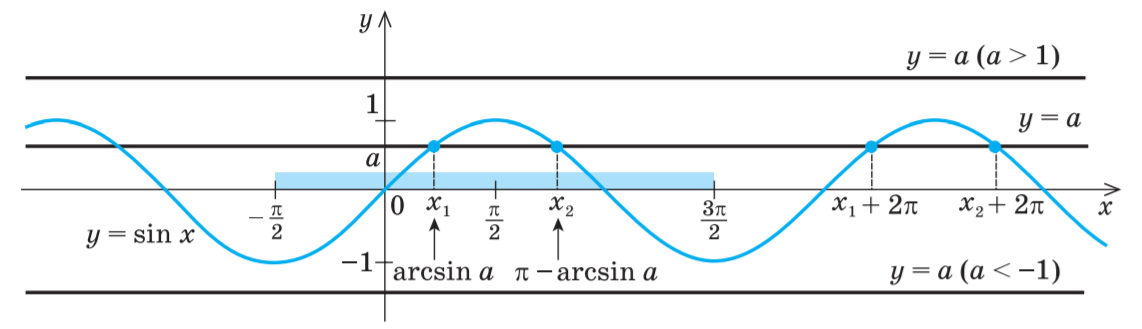
Пусть |a| ≤ 1. Тогда прямая y = a пересекает график функции y = sin x (рис. 1). На промежутке ![]() функция y = sin x возрастает от -1 до 1. Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение sin x = a имеет на этом промежутке только один корень, который по определению арксинуса равен: x1 = arcsin a (и для этого корня sin x = a).
функция y = sin x возрастает от -1 до 1. Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение sin x = a имеет на этом промежутке только один корень, который по определению арксинуса равен: x1 = arcsin a (и для этого корня sin x = a).
На промежутке ![]() функция y = sin x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение sin x = a имеет на этом промежутке только один корень x2 = π - arcsin a (рис. 1). Для проверки правильности записи значения второго корня x2 заметим, что x2 = π - x1, тогда sin x2 = sin (π- x1) = sin x1 = a. То есть x2 – корень уравнения sin x = a.
функция y = sin x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение sin x = a имеет на этом промежутке только один корень x2 = π - arcsin a (рис. 1). Для проверки правильности записи значения второго корня x2 заметим, что x2 = π - x1, тогда sin x2 = sin (π- x1) = sin x1 = a. То есть x2 – корень уравнения sin x = a.
Таким образом на промежутке ![]() (длиной 2π) уравнение sin x = a при |a| ≤ 1 имеет только корни x1 = arcsin a, x2 = π - arcsin a.
(длиной 2π) уравнение sin x = a при |a| ≤ 1 имеет только корни x1 = arcsin a, x2 = π - arcsin a.
Функция y = sin x периодическая с периодом 2π, поэтому все остальные корни отличаются от найденных 2πk (k ∈ Z). Получаем следующие формулы корней уравнения sin x = a при |a| ≤ 1:
x=arcsin a + 2πk, k ∈ Z. (1)
x= π - arcsin a + 2πk, k ∈ Z. (2)
Все значения корней уравнения sin x = a при |a| ≤ 1, которые дают формулы (1) и (2), можно записать с помощью одной формулы
x=(-1)n arcsin a + 2πn, n ∈ Z (3)
Действительно, из формулы (3) при четном n = 2k получаем x = arcsin a + 2πk – формулу (1), а при нечетном n = 2k +1 – формулу x= - arcsin a + π(2k+1)= π - arcsin a + 2πk, то есть формулу (2).
2.Частые случаи решения уравнения sin x = a.
Рисунок 2

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).
Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда
![]()
Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,
![]()
Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,
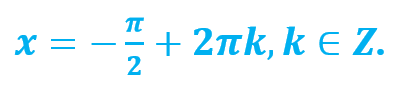
Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:
![]()


19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование
1.Корни уравнений tg x = a и ctg x = a
Рассмотрим уравнение tg x = a. На промежутке ![]() функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x1 = arctg a и для этого корня tg x = a.
функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x1 = arctg a и для этого корня tg x = a.
Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:
![]()
При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).
Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a.
Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:
![]()
При a = 0
![]()
таким образом, уравнение ctg x = 0 имеет корни
![]()
Примеры решения задач




Вопросы для контроля
Какие уравнения называют простейшими тригонометрическими?
Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
Выведите формулы решения простейших тригонометрических уравнений.
Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.
Упражнения
Решите уравнение

План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Тестовая работа №1
СПРАВОЧНЫЕ МАТЕРИАЛЫ.
Общие формулы для решения простейших тригонометрических уравнений:
1) sin t = a, (0πn, nϵZ.
2) sin t = -a, (0n+1 ∙ arcsin a +πn, nϵZ.
3) cos t = a, (0πn, nϵZ.
4) cos t = -a, (0π-arccos a)+2πn, nϵZ.
5) tg t = a, (a0); t = arctg a + πn, nϵZ.
6) tg t = -a, (a0); t = -arctg a + πn, nϵZ.
7) ctg t = a, (a0); t = arcctg a + πn, nϵZ.
8) ctg t = -a, (a0); t = π-arcctg a + πn, nϵZ.
Тестовая работа №1
Решить уравнение:
2 cos x + 3 = 0.
±arccos1,5+2πn, n∈Z;
B) нет решений;
C) -arccos1,5+2πn, n∈Z;
D) arcсos 3+2πn, n∈Z.
2. Решить уравнение:
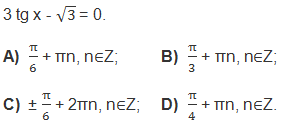
3. Решить уравнение:

4. Решите уравнение:

5. Найдите решение уравнения ctg x=1, принадлежащие интервалу (0; π).
A) π/3 ;
B) π/4;
C) 5π/4;
D) π.
6. Решите уравнение: 2 sin x = -1.

7. Найдите решение уравнения:

8. Решить уравнение: 3sin x -1= 0.

9. Решить уравнение:

10. Решить уравнение:
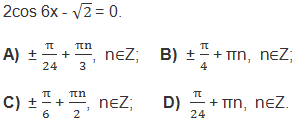
11. Решить уравнение: 2sin 3x–1 = 0.
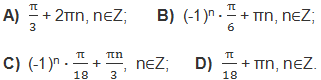
12. Решить уравнение:

13. Решите уравнение:
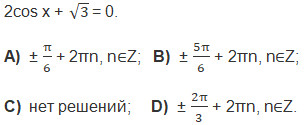
14. Найдите решение уравнения ctg x = -1, принадлежащие интервалу (0; π).
A) π/3;
B) π/4;
C) 3π/4;
D) 2π/3.
15. Решите уравнение:

План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Понятие о производной.
Тип урока - урок изучения нового материала.
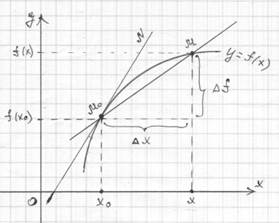
Пусть дан график функции у=f(x).
Рассмотрим точку М0 с абсциссой xo. Пусть ∆х – это изменение абсциссы от точки xo до х, т.е. ∆х = х – xo , M0М – секущая, M0N – касательная.
Найдите:
а) угловой коэффициент секущей (это средняя скорость изменения функции);
б) угловой коэффициент касательной (подсказка: касательная – это предельное положение секущей)
Решение: у= f(x) – заданная функция, ∆х = х – xo – изменение абсциссы от точки xo до х.
vср = ![]() . В нашем случае kсек =
. В нашем случае kсек =![]()
При х→х0 (или ∆х →0) будет f(x)→f(x0), следовательно, M0М→ M0N.
Тогда k кас = ![]() .
.

Рассмотрим движение материальной точки М по прямой с выбранным на ней началом отсчета – точкой О. Расстояние от начала отсчета до точки М в каждый момент времени t обозначим буквой s. Тогда движение точки М будет описываться функцией
s = s (t), t[ t0 ; t].
Найдите:
а) среднюю скорость за отрезок [t0 ; t];
б) скорость точки в момент времени t0 (мгновенную скорость).
Решение: За промежуток времени длительности t – t0 между моментами времени t0 и t точка проходит путь равный s(t) –s(t0 ).
Среднюю скорость получают, разделив перемещение материальной точки s на изменение времени, в течение которого оно совершено.
Тогда vср =![]() ;
;
Чем меньше рассматриваемый промежуток времени, тем точнее можно охарактеризовать движение. А мгновенной скоростью называется число к которому стремится разностное отношение средней скорости за промежуток времени от t0 до t при t→ t0.
Тогда vмгн = ![]() ,
,
Бактерии размножаются быстро и просто – они делятся пополам и при благоприятных условиях за сутки из одной бактерии могут образоваться десятки тысяч. Рост клеток бактерий в условиях ограниченности питательных веществ или пространства в течение начального интервала времени от t0 до t происходит по некоторому закону y = N(t).
Найдите:
а) среднюю скорость изменения количества бактерий за промежуток времени [t0 ; t];
б) скорость изменения количества точки в момент времени t0 (мгновенную скорость).
Решение: В физике для нахождения средней скорости делят длину перемещения тела s на время, в течение которого оно совершено,
т.е. vср =![]() . В нашем случае vср =
. В нашем случае vср =![]() .
.
Мгновенной скоростью v(t0) в момент времени t0 является число к которому стремится разностное отношение средней скорости за промежуток времени от t0 до t при t→ t0.
Тогда vмгн = ![]() .
.
4. Изучение нового материала
Приращению аргумента соответствует «приращение функции», которое также обозначается с помощью заглавной греческой буквы «∆».
Вопрос: Скажите, а вы знаете, кто впервые стал использовать знак «∆» для обозначения разности аргументов?
- Да. Буква «∆» – одна из заглавных букв греческого алфавита ее стал использовать Эйлер (сер. 18 века).
Исходя из этого полученную формулу можно записать по-другому: или и прочитать так: число, к которому стремится разностное отношение ![]() =
= ![]() при
при ![]() .
.
Поскольку многие задачи в различных областях науки в процессе решения приводят к такой же модели – этому отношению надо: дать название, дать обозначение и изучить его. Это мы с вами сейчас и сделаем.
(Слайд 4)
Определение: Производной функции ![]() в точке
в точке ![]() называется число, к которому стремится разностное отношение
называется число, к которому стремится разностное отношение ![]() =
= ![]() при
при ![]() .
.
но обозначается по-разному:
![]() х),
х), ![]() у′ – эти обозначения для производной ввел Жозеф Луи Лагранж
у′ – эти обозначения для производной ввел Жозеф Луи Лагранж
Это определение вы запишете в тетрадях.
Теперь посмотрите на ваши задачи и сформулируйте план нахождения производной.
(Учащиеся должны ответить):
(Слайд 5)
1. Задать функцию f(x).
Алгоритм нахождения производной (находим ![]() )):
)):
1) Задать приращение ![]() и вычислить
и вычислить ![]() =
= ![]() =
= ![]() .
.
2) Найти разностное отношение ![]() и сократить на
и сократить на ![]() .
.
3) Если ![]() при
при ![]() стремится к какому-то числу, то это число будет
стремится к какому-то числу, то это число будет ![]() .
.
Далее группа самостоятельно формулирует и записывает в тетради
Физический смысл производной – это скорость изменения расстояния: s‘(t) = v(t).
(За бесконечно малое время прошел бесконечно малое расстояние. Спидометр машины показывает мгновенную скорость. Скорость в данный момент времени ).
Если производная положительная, то расстояние увеличивается, а если отрицательная, то расстояние уменьшается.
(Слайд 6)
Геометрический смысл: f‘(хо) – это коэффициент угла наклона касательной к оси Ох
f‘(хо) = k = tg α.
(Слайд 7)
Т.е. из геометрического смысла получается, что если существует производная в точке хо, то можно провести что? (обычно ученики говорят: что можно провести касательную в точке хо и наоборот – если можно провести касательную в точке хо, то в этой точке существует производная. На ошибку в формулировке пока не обращается внимание, фраза записывается на доске в таком виде и дальше продолжаются обсуждения.
записывается под определением на доске
…Если существует производная в точке хо, то можно провести касательную в точке хо. Наоборот — если можно провести (…) касательную в точке хо, то в этой точке существует производная.
Итак, подведём итог: вы сами дали мне определение производной, но встаёт вопрос: а всегда ли существует производная в точке?
Особое внимание обращается на моменты, когда касательная перпендикулярна оси Ох и параллельна оси Ох.
Всегда ли существует ли производная в точке хо?
Задается ряд вопросов:
| Если касательная к графику функции будет убывающей, то каким будет угол между этой прямой и осью Ох? | Угол будет тупым. |
| Каким будет угловой коэффициент k ? | k |
| Если касательная к графику функции будет возрастающей, то каким будет угол между этой прямой и осью Ох? | Угол будет острым. |
| Каким будет угловой коэффициент k ? | k 0 |
| Если касательная к графику функции будет параллельна оси Ох или совпадать с ней, то каким будет угол между этой прямой и осью Ох? | Угла не будет, вернее α = 0º |
| Чему равен тангенс угла наклона такой касательной? | tg 0º = 0 |
| Чему равен угловой коэффициент k касательной, параллельной оси Ох? | Также не существует! |
| Чему равен угол наклона вертикальной касательной? | α = 90º |
| Чему равен тангенс угла наклона вертикальной касательной? | tg 90º не существует. Почему? Потому, что cos 90º = 0… |
| Чему равен угловой коэффициент k вертикальной касательной? | Также не существует! |
Давайте вернёмся к геометрическому смыслу производной: производная в точке равна угловому коэффициенту касательной, проведённой в этой точке f‘(хо) = k = tg α.
| Если в точке можно провести невертикальную касательную, то в этой точке существует производная, и наоборот, если в точке существует производная, то в этой точке можно провести невертикальную касательную |
5. Закрепление нового материала
Самостоятельная работа в группах (15-20 минут)
Вот теперь вы готовы к работе с производной и можете приступить к выполнению задания №2
Биологи

Пользуясь определением и схемой вычисления производной, найдите производную функции y = C.
Решение
y = C – постоянная линейная функция.
∆у = f(x +∆х) – f(x)= С – С = 0;
то у′ = 0.
Итак, ( С ) ′= 0.
Физики

Пользуясь определением и схемой вычисления производной, найдите производную функции y = kx + b.
Решение
y = kx + b – линейная функция.
Аргументу х дадим приращение ∆х, тогда
∆у = f(x + ∆х) – f(x)=
= k (x +∆х)+ b – (kx + b) = k∙x + k∆∙х – kx – b = k∆∙х
= k = k.
Итак, (kx + b)′ = k.
Математики
Лист №2: Пользуясь определением и схемой вычисления производной, найдите производную функции y = х2.
Решение
y = х2 .
Аргументу х дадим приращение ∆х, тогда
∆у = f(x + ∆х) – f(x)=
= (x +∆х)2 – х2 =
= х2+ 2∙х∙∆х + (∆х)2 – х2 = 2∙х∙∆х + (∆х)2 = ∆х∙(2х +∆х)
= 2х = 2х.
Итак, (х2 )′ = 2х.
6 этап. Закрепление нового понятия
1) Откройте учебники на стр. 106, № 189(а,б)
2) Возьмите лист № 3. Задания из ЕГЭ
Лист № 3.
1. Задание 7 (№ 9649)
На рисунке изображены график функции y = f(x) и
касательная к нему в точке с абсциссой x0 . Найдите
значение производной функции f = (x) в точке x0 .

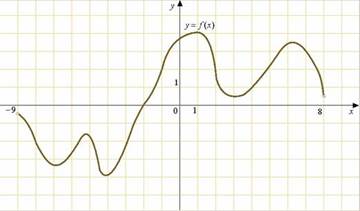
2. Задание B7 (№ 6399)
На рисунке изображен график функции ![]() , определенной на интервале
, определенной на интервале ![]() . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции ![]() положительна.
положительна.
7 этап. Итог урока
8 этап. Домашнее задание
№188 (б)
Постройте график функции f и проведите к нем касательную, проходящую через точки с абсциссой x0. Пользуясь рисунком, определите знак углового коэффициента этой касательной.
б) ![]()
№189 (в, г)
Определите знак углового коэффициента касательной, проведенной к графику функции через точки с абсциссой ![]() (если касательная существует).
(если касательная существует).
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Производные элементарных функций.
Перечень вопросов, рассматриваемых в теме
1) определение элементарной функции;
2) производная показательной функции;
2) производные тригонометрических функций;
3) производная логарифмической функции.

Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации.
(ex) '= ex
(ekx+b) '=kekx+b
(ax) '=axlna
![]()
![]()
![]()
(sin x) '=cosx
(cos x) '= -sinx
Теоретический материал для самостоятельного изучения
Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации. При решении многих практических задач часто приходится находить производные таких функций.
1.Производная показательной функции.
Показательная функция f(x)=ax, где а0, a ≠1, определена на всей числовой прямой и имеет производную в каждой ее точке. Любую показательную функцию можно выразить через показательную функцию с основанием у по формуле:
ax=exln a (1)
так как exln a= (eln a)х= ах.
Стоит отметить свойств о функции ех: производная данной функции равна ей самой
(ex) '= ex. (2)
Применяя правило дифференцирования сложной функции, получим:
(ekx+b) ' = kekx+b. (3)
Производная для ax:
(ax) ' = axlna. (4)
2.Производная логарифмической функции.
Логарифмическую функцию ![]() с любым основанием а 0, а≠ 1 можно выразить через логарифмическую функцию с основанием е с помощью формулы перехода
с любым основанием а 0, а≠ 1 можно выразить через логарифмическую функцию с основанием е с помощью формулы перехода
![]() (5)
(5)
Производная функции lnх выражается формулой
![]() (6)
(6)
Применяя правило дифференцирования сложной функции, получаем
![]() (7)
(7)
![]() (8)
(8)
3.Производные тригонометрических функций.
Для тригонометрических функций справедливы следующие равенства:
(sin x)’=cosx (9)
(cos x)’= -sinx (10)
Примеры и разбор решения заданий тренировочного модуля
Найти производную:
f(x) = 3lnx
Решение: ![]()
Ответ: ![]()
f(x) = 3·e2x
Решение: (3e2x) ' = 3·2· e2x = 6 ·e2x
Ответ: 6 ·e2x
f(x) = 2x
Решение: (2x) ' = 2xln2
Ответ: 2xln2
![]()
Решение: ![]()
Ответ: ![]()
f(x) = sin (2x+1) - 3cos(1-x)
Решение: (sin (2x+1) - 3cos(1-x)) ' = 2cos(2x+1) - 3sin(1-x)
Ответ: 2cos(2x+1) - 3sin(1-x)
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока : Перпендикулярность прямых в пространстве .
Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой..

Доказательство:Дано: a ‖ b, a ⊥ c
Доказать: b ⊥ c .Через точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с. Так как а ⊥ с, то ∠АМС=90о.
Так как b ‖ a, а а ‖ МА, то b ‖ МА. Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между ними равен 90о, т.е. b ‖ МА, с ‖ МС, угол между МА и МС равен 90о .Это означает, что угол между прямыми b и с также равен 90о, то есть b ⊥ с. Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
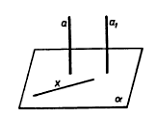
Доказательство:Дано: a ‖ а1, а ⊥ α
Доказать, что а1 ⊥ α
Проведем какую-нибудь прямую x в плоскости α, т.е. x ∊ α.Так как а ⊥ α, то а ⊥ x.По лемме о перпендикулярности двух параллельных прямых к третьей а1 ⊥ x.Таким образом, прямая а1 перпендикулярна к любой прямой, лежащей в плоскости α, т. е. а1 ⊥ α .Теорема. Ели две прямые перпендикулярны плоскости, то они параллельны.
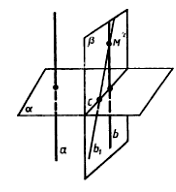
Дано: а ⊥ α, b ⊥ α
Доказать, что а ‖ b
Доказательство:Через какую-нибудь точку М прямой b проведем прямую b1, параллельную прямой а.
М ∊ b, M ∊b1, b1 ‖ a. По предыдущей теореме b1 ⊥ α. Докажем, что прямая b1 совпадает с прямой b. Тем самым будем доказано, что а ‖ b. Допустим, что прямые b1 и b не совпадают. Тогда в плоскости β, содержащей прямые b и b1, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а ‖ b, т.е. b ∊ β, b1 ∊ β, α ![]() β = c (невозможно)→ а ‖ b . Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.
β = c (невозможно)→ а ‖ b . Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.
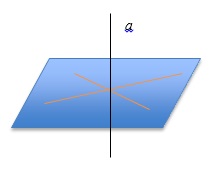 Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Рис. 2.
Доказательство.
Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку М проходит единственная прямая с, перпендикулярная плоскости α. Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b – линия пересечения плоскостей α и γ.

Рис. 3.
В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.
Домашнее задание : Тестовая работа .
1)Выбор элемента из выпадающего списка
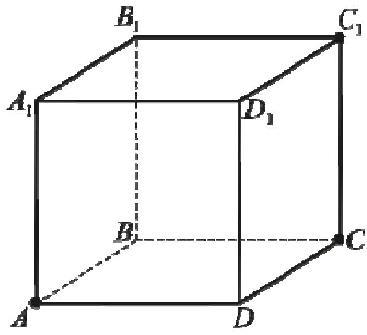
Выпишите ребра, перпендикулярные плоскости (DC![]() ).
).
Варианты ответов:
1)AD, A1D1, BC, B1C1
2)AD, AC, AD1,
3)ВС, ВА.
Пример 2
Утверждение:
Две прямые называются перпендикулярными, если …..
Варианты ответов:
1)![]()
2)![]()
3)параллельны
4)она перпендикулярна к любой прямой, лежай в этой плоскости.
5)перпендикулярна плоскости.
Пример 3
Утверждение
Если плоскости перпендикулярна одной из двух параллельных прямых, то она ……
Варианты ответов:
1)![]()
2)![]()
3)параллельны
4)она перпендикулярна к любой прямой, лежай в этой плоскости.
5)перпендикулярна плоскости.
Пример 4
Указать верный ответ:
1) Две прямые имеют общую плоскость, через которые можно провести плоскость.
2) Провести плоскость если две прямые не имеют общую точку.
3) Если две различные прямые имеют общую точку, то через них можно провести плоскость.
4) Если две различные плоскости имеют общую точку, то они не пересекаются.
Пример 5
Прямая перпендикулярная к двум различным плоскостям, тогда плоскости:
1) пересекаются 2) скрещиваются 3) параллельны 4) нельзя определить
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока : Перпендикулярность и наклонная .
Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.

(Рис. 1)
Рассмотрим прямоугольный треугольник АМН. Сторона АН — катет, а сторона AM — гипотенуза, поэтому АН AM. Поэтому перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости. Следовательно, из всех расстояний от точки А до различных точек плоскости α наименьшим является расстояние до точки Н. Это расстояние, т. е. длина перпендикуляра, проведенного из точки А к плоскости α, называется расстоянием от точки А до плоскости α.
Стоит отметить, что в случае двух параллельных плоскостей, расстоянием между ними будет расстояние от произвольной точки одной плоскости до другой плоскости. Например, все точки потолка находятся на одинаковом расстоянии от пола. Если же прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. В этом случае расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью. Например, все точки прямой b равноудалены от потолка комнаты. Если мы имеем дело со скрещивающимися прямыми, то расстоянием между ними будет расстояние между одной из этих прямых и плоскостью, проходящей через другую прямую параллельно первой.
Сформулируем теорему о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

(Рис. 2)
На рисунке 2: АН — перпендикуляр к плоскости α, AM — наклонная, а — прямая, проведенная в плоскости α через точку М перпендикулярно к проекции наклонной НМ. Докажем, что прямая а перпендикулярна наклонной AM.
Рассмотрим плоскость АМН. Прямая а перпендикулярна к НМ по условию. Так как прямая а, лежит в плоскости α, а эта плоскость перпендикулярна отрезку AH, то прямая а перпендикулярна к этой плоскости. Отсюда следует, что прямая а перпендикулярна к любой прямой, лежащей в плоскости АМН, в частности прямая а перпендикулярна отрезку АМ. Теорема доказана.
Эта теорема называется теоремой о трех перпендикулярах, так как в ней говорится о связи между тремя перпендикулярами АН, НМ и AM.
Справедлива также обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Введем теперь понятие проекции произвольной фигуры на плоскость. Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
Обозначим буквой F какую-нибудь фигуру в пространстве. Если мы построим проекции всех точек этой фигуры на данную плоскость, то получим фигуру F1, которая называется проекцией фигуры F на данную плоскость (рис. 3).
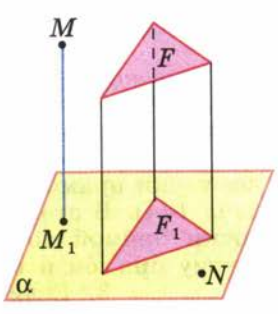
(Рис. 3)
Докажем теперь, что проекцией прямой на плоскость, не перпендикулярную к этой прямой, является прямая (рис. 4).
Данную плоскость обозначим буквой α. Произвольную прямую, не перпендикулярную к плоскости, обозначим буквой а. Из какой-нибудь точки М прямой а проведем перпендикуляр МН к плоскости α и рассмотрим плоскость β, проходящую через прямую a и перпендикуляр МН. Плоскости α и β пересекаются по некоторой прямой а1.
Докажем, что эта прямая и является проекцией прямой а на плоскость α. В самом деле, возьмем произвольную точку М1 прямой а и проведем в плоскости β прямую М1Н1, параллельную прямой МН.
Так как отрезок MH перпендикуляр к плоскости α и отрезок MH параллелен М1Н1, то отрезок М1Н1 тоже перпендикулярен плоскости α.
Этим мы доказали, что проекция произвольной точки прямой а лежит на прямой а1.
Аналогично доказывается, что любая точка прямой а1 является проекцией некоторой точки прямой а. Следовательно, прямая а1 — проекция прямой а на плоскость α. Что и требовалось доказать.
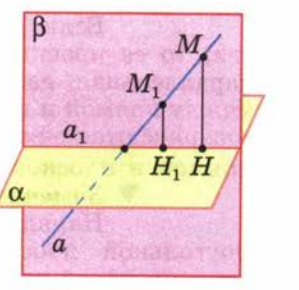
(Рис. 4)
Теперь введем понятие угла между прямой и плоскостью.
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Виды соединений – сочетания, размещение, перестановки, факториал, связь между ними.
КРАТКАЯ ТЕОРИЯ
Комбинаторика – это раздел математики, в котором изучается, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов.
Все комбинаторные формулы можно вывести из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения. Эти два важных правила часто применяются при решении комбинаторных задач.
Основными понятиями комбинаторики являются размещения, перестановки и сочетания.
Размещением из n элементов по m называется любое упорядоченное подмножество, состоящее из m различных элементов данного множества.
Число размещений (без повторений) из n элементов по m элементам равно
Пример 1. Сколькими способами можно выбрать председателя, заместителя и профорга из 9 человек?
Решение. n = 9, m = 3.
Перестановкой из n элементов называется размещение из n элементов по n элементам.
Число перестановок n различных элементов (без повторений) равно Рn=n!
Пример 3. В соревнованиях по фигурному катанию принимали участие россияне, итальянцы, украинцы, немцы, китайцы и французы. Сколькими способами могут распределиться места по окончании соревнований?
Решение. Используем формулу перестановки без повторения для n = 6:
Р6=6! = 1*2*3*4*5*6 = 720
Сочетанием из n элементов по m называется любое подмножество, состоящее из m различных элементов данного множества
Число сочетаний из n элементов по m(без повторений) равно
Пример 5. Из учащихся 25 человек нужно выбрать троих дежурных. Сколькими способами это можно сделать?
Решение. n = 25, m = 3.
Домашнее задание:
1.
Сколькими способами могут восемь человек стать в очередь к театральной кассе?
Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов может он выбрать?
2.
Сколько различных перестановок можно образовать из всех букв слова «Абракадабра»?
Сколько различных перестановок можно образовать из всех букв слова «Тарантас»?
3.
Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?
Сколькими способами можно выбрать 4 краски из имеющихся 9 различных красок?
4.
Имеется 10 различных книг и 15 различных журналов. Сколькими способами можно составить посылку из 3 книг и 5 журналов?
На первой полке стоит 12 книг, а на второй 10. Сколькими способами можно выбрать 4 книги с первой полки и 3 со второй?
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Понятие вероятности события.
КРАТКАЯ ТЕОРИЯ
Согласно классическому определению вероятности вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Вероятность события А определяется формулой:
Р(А) = m/n,
где m – число элементарных исходов, благоприятствующих А;
n – число всех возможных элементарных исходов испытания.
Пример 1. В ящике имеется 10 красных и 8 синих шаров. Наудачу вынимают один шар. Найти вероятность того, что извлеченный шар окажется синим.
Решение.
Дано:
m= 7
n = 10+8 = 18
Решение
А – извлеченный шар синего цвета
P(A) = m/n = 7/18 = 0,38 = 38,9%
Р(А) - ?
Ответ: P(A) = 38,9%
Пример 2. В мешочке имеется 6 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, р, ф, а, ь, н.Найти вероятность того, что на вынутых по одному и расположенных в одну линию кубиках можно будет прочесть слово «фонарь».
Решение.
Дано:
о, р, ф, а, ь, н
Решение
А – из кубиков сложилось слово «фонарь».
P(A) = m/n
Т.к. из данных букв слово «фонарь» можно сложить только одним способом, то событию Aблагоприятствует 1 исход. → m= 1.
Количество всех возможных способов выпадения букв на кубиках равно количеству перестановок.
n= P6 = 6! = 1*2*3*4*5*6 = 720
P(A) = 1/720 = 0,00139 = 1,4%
Р(А) - ?
Ответ: P(A) = 1,4%
Домашнее задание:
1.
В коробке лежат 6 красных и 4 синих карандаша. Наугад вытаскиваются один из них. Найти вероятности событий того, что извлеченный карандаш красного цвета.
В коробке лежат 3 красных, 6 синих и 5 зеленых карандашей. Наугад вытаскиваются один из них. Найти вероятности событий того, что извлеченный карандаш красного цвета.
2.
Бросаются два игральных кубика.Какова вероятность, что сумма выпавших очков равна 6.
3.
Бросаются два игральных кубика.Какова вероятность, что сумма выпавших очков равна 8.
4.
В пачке находятся одинаковые по размеру 10 тетрадей в линейку и 6 в клетку. Из пачки наугад берут 4 тетради. Какова вероятность того, что все 4 тетради окажутся в клетку?
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛОЖНЫХ СОБЫТИЙ С ПОМОЩЬЮ ТЕОРЕМ УМНОЖЕНИЯ И СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
КРАТКАЯ ТЕОРИЯ :
Суммой A + B двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий.
Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, равна сумме вероятностей этих событий:
Р (А + В) = Р(А) + Р(В)
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А+В) = Р(А) + Р(В) – Р(АВ)
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении этих событий.
Теорема произведения для независимых событий. Для независимых событий вероятность совместного появления событий равна произведению вероятностостей этих событий:
Р(АВ) = Р(А) Р(В).
Домашнее задание:
1.
Среди сотрудников фирмы 28% знают английский язык, 30% – немецкий; английский и немецкий – 8%. Найти вероятность того, что случайно выбранный сотрудник фирмы знает хотя бы один язык.
2.
Имеется 3 ящика, содержащих по 20 деталей. В первом ящике 12, во втором 5 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все детали окажутся стандартными.
3.
Имеется 3 ящика, содержащих по 15 деталей. В первом ящике 5, во втором 7 и в третьем 10 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все детали окажутся стандартными
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: « Логарифмической функции».
Конспект урока .
Напомним, что логарифмической называется функция вида ![]() , где
, где ![]() ,
, ![]() . Здесь
. Здесь ![]() – независимая переменная, аргумент;
– независимая переменная, аргумент; ![]() – зависимая переменная, фунция;
– зависимая переменная, фунция; ![]() – основание, фиксированное число.
– основание, фиксированное число.
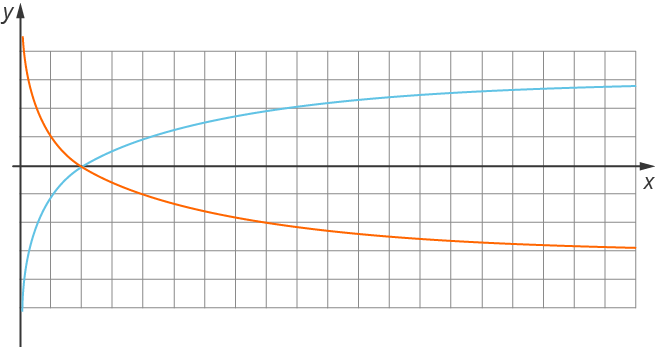
Рис. 1 – график логарифмической функции при ![]() (черный) и
(черный) и ![]() (красный)
(красный)
Основные свойства логарифмической функции:
1) Область определения: ![]() ,
, ![]() ;
;
2) Область значений: ![]() ,
, ![]() ;
;
3) ![]() ;
;
4) при ![]() функция возрастает, при
функция возрастает, при ![]() – убывает;
– убывает;
Итак, под знаком логарифма может стоять только положительное число, причем любое. Сам же логарифм может принимать абсолютно любые значения. Логарифм единицы при любом основании равен нулю, то есть все логарифмические кривые проходят через фиксированную точку ![]() .
.
Монотонность логарифмической функции
Мы многократно указывали на монотонность логарифмической функции, но никогда не доказывали этот факт. Рассмотрим на конкретном примере и тогда станет понятно, как для любой логарифмической функции доказать факт ее монотонного возрастания или убывания.
Задача:Доказать, что функция ![]() монотонно возрастает. Доказательство:
монотонно возрастает. Доказательство:
Напомним, что ![]() (выражение 1) является корнем уравнения
(выражение 1) является корнем уравнения ![]() (выражение 2). Подставим значение
(выражение 2). Подставим значение ![]() из выражения 1 вместо
из выражения 1 вместо ![]() в выражение 2 и получим основное логарифмическое тождество:
в выражение 2 и получим основное логарифмическое тождество:
![]() Напомним, что здесь
Напомним, что здесь ![]() ,
, ![]() ,
, ![]()
Утверждение, что функция монотонно возрастает, означает, что большему значению аргумента соответствует большее значение функции: ![]() . Запишем
. Запишем ![]() и
и ![]() с помощью основного логарифмического тождества:
с помощью основного логарифмического тождества:
![]() ,
, ![]()
Мы выбрали ![]() и
и ![]() из области определения, то есть оба эти числа положительны, так, что
из области определения, то есть оба эти числа положительны, так, что ![]() :
: ![]()
Имеем:
![]()
Получили показательное неравенство, в котором основания степеней равны и больше единицы, значит, имеем право сравнить показатели, сохранив при этом знак неравенства:
![]()
Что и требовалось доказать.
Решение простейших уравнений и неравенств
Перейдем к решению типовых задач.
Пример 1 – решить уравнение, неравенство:
а) ![]()
б) ![]()
в) ![]()
Рассмотрим график логарифмической функции ![]() :
:
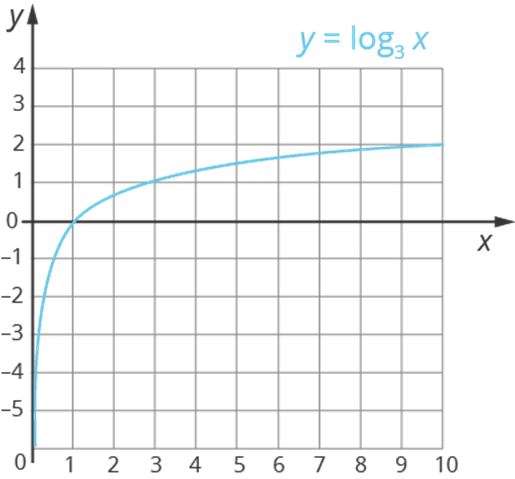
Рис. 2 – график функции ![]()
Очевидно, что функция возрастает.
Решим уравнение:
![]()
Пример а) решен. Итак, заданная функция имеет единственный корень и вся область определения разбивается этим корнем на два интервала: первый интервал ![]() , здесь функция отрицательна, кривая находится под осью; второй интервал
, здесь функция отрицательна, кривая находится под осью; второй интервал ![]() , здесь функция положительна, кривая находится над осью. Ответ очевиден.
, здесь функция положительна, кривая находится над осью. Ответ очевиден.
Ответ: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]()
Решим аналогичную задачу.
Пример 2:
а) ![]()
б) ![]()
в) ![]()
Рассмотрим график логарифмической функции ![]() :
:

Рис. 3 – график функции ![]()
Очевидно, что функция убывает.
Решим уравнение: ![]()
Пример а) решен.
Итак, заданная функция имеет единственный корень и вся область определения разбивается этим корнем на два интервала: первый интервал ![]() , здесь функция положительна, кривая находится над осью; второй интервал
, здесь функция положительна, кривая находится над осью; второй интервал ![]() , здесь функция отрицательна, кривая находится под осью. Ответ очевиден.
, здесь функция отрицательна, кривая находится под осью. Ответ очевиден.
Ответ: а) ![]() ; б)
; б)![]() ; в)
; в) ![]()
Список рекомендованной литературы.
1) Мордкович А.Г. Алгебра и начала математического анализа. М.: Мнемозина
2) Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. М.: Дрофа.
3) Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. М.: Просвещение.
Рекомендованные ссылки на ресурсы интернет:
1) Интернет-сайт «ГлавСправ» (Источник)
2) Интернет-сайт Nado5.ru (Источник)
3) Интернет-сайт UzTest.ru (Источник)
Домашнее задание.
Пример 1 – построить график функции:
а) ![]()
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: «Решение логарифмических уравнений».
Конспект урока .
Логарифмические уравнения
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы. Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
![]() . При этом
. При этом ![]() .
.
Обратим внимание на область допустимых значений логарифма:![]() .
.
Основное логарифмическое тождество: ![]() ,
, ![]() .
.
Основные формулы для логарифмов:
![]() (Логарифм произведения равен сумме логарифмов)
(Логарифм произведения равен сумме логарифмов)
![]() (Логарифм частного равен разности логарифмов)
(Логарифм частного равен разности логарифмов)
![]() (Формула для логарифма степени)
(Формула для логарифма степени)
Формула перехода к новому основанию:
![]()
![]() .
.
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
1.Решите уравнение: ![]()
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Получаем: ![]()
![]() Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение ![]() определено при
определено при ![]() .
.
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение: ![]()
В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде ![]() . Дальше все просто.
. Дальше все просто.
Ответ: -124
3. Решите уравнение: ![]()
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
![]() ;
;
![]() ;
;
![]() ;
;
![]()
4. Решите уравнение: ![]()
Область допустимых значений: ![]() Значит,
Значит, ![]()
Представим 2 в правой части уравнения как ![]() — чтобы слева и справа в уравнении были логарифмы по основанию 5.
— чтобы слева и справа в уравнении были логарифмы по основанию 5.
![]()
Функция ![]() монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом
монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом ![]() .
.
![]()
![]() . Ответ: 21.
. Ответ: 21.
Домашнее задание .
7.Решите уравнение: ![]() .
.
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: « Логарифмической функции».
Конспект урока .
Схема решения логарифмических неравенств
На предыдущем уроке мы рассмотрели решение логарифмических уравнений и их систем. На этом уроке речь пойдет о логарифмических неравенствах и их системах.
Мы уже говорили о логарифмической функции и ее свойствах. Важным свойством, которым мы пользовались для решения логарифмических уравнений: монотонность.
Для ![]() график логарифмической функции выглядит следующим образом:
график логарифмической функции выглядит следующим образом:
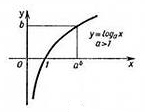
![]() - возрастающая функция: чем больше
- возрастающая функция: чем больше ![]() , тем больше
, тем больше ![]() . Значит,
. Значит, ![]() . В отличие от уравнений, здесь проверкой обойтись не удастся, поэтому необходимо учитывать ОДЗ:
. В отличие от уравнений, здесь проверкой обойтись не удастся, поэтому необходимо учитывать ОДЗ: ![]() .
.
Объединяя, получаем: ![]() .
.
![]()
Для ![]() график логарифмической функции выглядит следующим образом:
график логарифмической функции выглядит следующим образом:

![]() - убывающая функция: чем больше
- убывающая функция: чем больше ![]() , тем меньше
, тем меньше ![]() . Значит,
. Значит, ![]() .
.
ОДЗ: ![]() .
.
Объединяя, получаем: ![]()
![]() .
.
Проверка ОДЗ при решении логарифмических неравенств
Лучше всего начинать решение неравенств с проверки ОДЗ. Поскольку даже на первом шаге решения можно получить выражение с измененной ОДЗ.
Например:
![]()
ОДЗ: ![]()
![]()
![]()
А после преобразований: ![]()
ОДЗ: ![]()
|
|
|
|
|
|
![]()
Как быстро определить знак логарифма
Рассмотрим такой полезный факт: как быстро определить знак логарифма?
Рассмотрим два случая:
1) ![]() :
: ![]()
2) ![]() :
: ![]()
Таким образом, ![]() , если
, если ![]() и
и ![]() лежат по одну сторону от 1, и
лежат по одну сторону от 1, и ![]() , если
, если ![]() и
и ![]() лежат по разные стороны от 1.
лежат по разные стороны от 1.
Основные виды логарифмических неравенств
1) Простейшие ![]()
2) Сводящиеся к простейшим ![]()
3) С использованием свойств логарифмов ![]()
4) С заменой ![]()
5) С переменной в основании ![]()
Системы логарифмических неравенств
1.Решить неравенство:
![]()
ОДЗ:
![]()
![]()
Решение:
![]()
Так как основание логарифма больше 1, то знак неравенства сохраняем:
![]()
![]()
![]()
Ответ: ![]()
2.Решить неравенство:
![]()
ОДЗ:
![]()
![]()
Решение:
![]()
Так как основание логарифма меньше 1, то знак неравенства меняем:
![]()
![]()
![]()
Пересекаем решение и ОДЗ, имеем: ![]()
Полезные ссылки:
1) Алгебра 11 класс: "Логарифмические неравенства"
2) Алгебра 11 класс: "Решение логарифмических неравенств"
3) Алгебра 11 класс: "Решение логарифмических неравенств (продолжение)"
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: « Показательные и Логарифмические функции».
Конспект урока .
1. Показательной называют функцию вида y = ах,где а – основание, a 0,а ≠ 1;
х – показатель,
Свойства показательной функции y = ах, а ≠ 1, a 0
D(х) = (-∞; +∞),
E(y) = (0; +∞).
Нулей не имеет;
Точка пересечения с осью Оу:(0; 1),т. к. у(0) = а0 = 1.
При а 1 функция возрастает; при 0
Ни чётная функция, ни нечётная.
Не ограничена сверху, ограничена снизу прямой у = 0.
Не имеет ни наибольшего, ни наименьшего значений.
Непрерывна.
Выпукла вниз.
Примеры функций:;.
Графики показательной функции y = ах, а ≠ 1, a 0

2. Логарифмической называют функцию вида , где а – основание логарифма, а ≠ 1, a 0;
Свойства логарифмической функции y = logах, а ≠ 1, a 0
D(х) = (0; +∞),
E(y) = (-∞; +∞)
Ни четная функция, ни нечетная.
Нули функции: у = 0 при х = 1;
Точек пересечения с осью ординат Оу нет.
При а 1 функция возрастает на (0; +∞);
при 0
Не ограничена сверху, не ограничена снизу. Ось Оу является вертикальной асимптотой графика логарифмической функции.
Не имеет ни наибольшего, ни наименьшего значений.
Непрерывна.
При а 1 функция выпукла вверх; при 0
Графики логарифмической функции у = logax, а 0

Примеры функций:;.
Для того чтобы сопоставить функции у = ах и у = logax при а 0, а ≠ 1 нужно хорошо представлять, что такое показательная и логарифмическая функции. А вспомнить эти понятия поможет следующий тест.
Тест.
2
![]()
1) 3 и 4;
2) 2, 3 и 5;
3) 3 и 5;
4) 4.
2. Какие из данных функций являются показательными:
![]()
1) 3 и 4;
2) 2, 3 и 5;
3) 3 и 5;
4) 4.
3. Назовите возрастающие функции:
![]()
1) 1,3 и 7;
2) только 1 и 7;
3) 2, 4, 5 и 6;
4) 2, 4 и 6.
4. Назовите убывающие функции:
![]()
1) 1,3 и 7;
2) только 1 и 7;
3) 2, 4, 5 и 6;
4) 2, 4 и 6.
5. Какая из линий на рис.1 является графиком является графиком функции у = log7x?
1) а;
2) б;
3) в;
4) г.
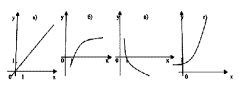
Рисунок 1.
6. Областью значений логарифмической функции является множество действительных чисел.
1) да;
2) нет.
7. Областью определения показательной функции является множество действительных чисел.
1) да;
2) нет.
8. Логарифмическая функция у = logax и показательная функции у = ах при а 0, а ≠ 1.
1) степенные;
2) взаимно обратные;
3) линейные.
9. Сами же функции порою убывают, порою по команде возрастают. А командиром служит им значение …, и подчиняются они ему всегда.
1) такого значения нет;
2) х;
3) а.
10. Область значения функции у = 3х + 1 числовой промежуток:
1) (-4;4);
2) (0;+∞);
3) (-∞; +∞);
4) (1;+∞).
11. Функции у = ах и у = logax при а 0, а ≠ 1 симметричны относительно:
1) прямой у = х;
2) оси Оу;
3) оси Ох.
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Понятие неравенство. Решение неравенства.
1. Виды неравенств и их решение.
| Вид неравенства | Решение |
| Линейные |
|
| Содержащие чётную степень |
|
| Содержащие нечётную степень |
|
| Иррациональные |
|
| Иррациональные |
|
| Показательные |
|
| Логарифмические |
|
| Тригонометрические | При решении используют тригонометрическую окружность или график соответствующей функции |
2. Равносильность неравенств.
Перечислим некоторые преобразования неравенств, приводящие данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел.
Перенос члена неравенства (с противоположным знаком) из одной части неравенства в другую;
Умножение (деление) обеих частей неравенства на положительное число;
Применение правил умножения многочленов и формул сокращённого умножения;
Приведение подобных членов многочлена;
Возведение неравенства в нечётную степень;
Логарифмирование неравенства ![]() , т.е замена этого неравенства неравенством
, т.е замена этого неравенства неравенством![]()
Назовем преобразования неравенств, приводящие исходное неравенство к неравенству равносильному ему на некотором множестве чисел
Возведение неравенства в чётную степень; (на множестве где обе функции неотрицательны)
Потенцирование неравенства; (на множестве где обе функции положительны)
Умножение обеих частей неравенства на функцию; (на множестве где функция положительна)
Применение некоторых формул (логарифмических, тригонометрических и др.) (на множестве где одновременно определены обе части применяемой формулы)
В зависимости от интерпретации неравенства различают
алгебраический
функциональный
графический
геометрический.
Среди алгебраических методов решения неравенств выделяют:
Сведение неравенства к равносильной системе или совокупности систем
Метод замены
Разбиение области определения неравенства на подмножества
Логарифмическое неравенство ![]() можно свести к равносильной совокупности систем неравенств
можно свести к равносильной совокупности систем неравенств
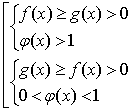
Решите неравенство:
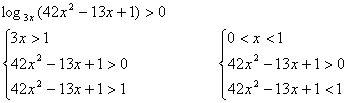

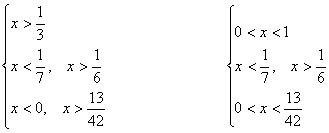
![]()
Ответ: ![]()
Оказывается, что данное неравенство можно решить иначе.
Зная свойства логарифма о том, что logа b 0, если a и b по одну сторону от 1, можно получить очень интересный и неожиданный способ решения неравенства. Об этом способе написано в статье “Некоторые полезные логарифмические соотношения” в журнале “Квант” № 10 за 1990 год.

Решите это неравенство, используя новые соотношения

Ответ: ![]()
Оказывается, что при решении некоторых логарифмических неравенств можно использовать и другие соотношения
развернуть таблицу
| Заменяемое выражение | Используемое выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
развернуть таблицу
Решите неравенство ![]()
у доски составляем систему, которую решают самостоятельно
![]()
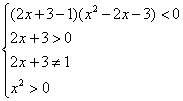
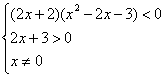
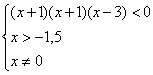
![]()
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока : Простейшие показательные неравенстваКонспект урока
Пример №1. Решить неравенство: ![]()
Правило: привести к одинаковому основанию.
![]()
Так как основание больше 1, знак неравенства не меняется ![]()
![]() Ответ:
Ответ: ![]()
Пример №2. Решить неравенство: ![]()
![]()
Так как основание больше 1, знак неравенства не меняется ![]()
![]()
Ответ: ![]()
Пример №3. Решить неравенство: ![]()
![]()
Так как основание меньше 1, знак неравенства меняется ![]()
![]()
Ответ: ![]()
Показательные неравенства, которые сводятся к простейшим
Пример №1. ![]()
![]()
Так как основание меньше 1, знак неравенства меняется ![]()
![]()
![]()
![]()
Ответ:![]()
Пример №3. Решите неравенство ![]()
Подсказка: чтобы не ошибиться, лучше приводить обе части неравенства к основанию больше 1, так как в этом случае нет риска забыть о смене знака неравенства.
Вспомним, что: ![]()
Поэтому: ![]()
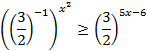
![]()
Так как основание больше 1, знак неравенства не меняется ![]()
![]()
![]()
![]()
![]()

Ответ: ![]()
Пример №4. Решите неравенство ![]()
Приведем обе части неравенства к основанию 2: ![]()
![]()
![]()
![]()
Так как основание больше 1, знак неравенства не меняется ![]()
![]()
![]()
![]()
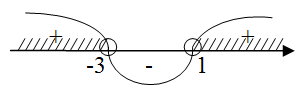
Ответ: ![]()
Сводящиеся к квадратным
Пример №1. Решите неравенство: ![]()
Замена: ![]()
![]()
![]()
![]()

![]()
Обратная замена:
![]()
![]()
Ответ: ![]()
Домашнее задание : Решите неравенство: ![]()
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Решения логарифмических неравенств.
Конспект урока
На предыдущем уроке мы рассмотрели решение логарифмических уравнений и их систем. На этом уроке речь пойдет о логарифмических неравенствах и их системах.
Мы уже говорили о логарифмической функции и ее свойствах. Важным свойством, которым мы пользовались для решения логарифмических уравнений: монотонность.
Для ![]() график логарифмической функции выглядит следующим образом:
график логарифмической функции выглядит следующим образом:

![]() - возрастающая функция: чем больше
- возрастающая функция: чем больше ![]() , тем больше
, тем больше ![]() . Значит,
. Значит, ![]() . В отличие от уравнений, здесь проверкой обойтись не удастся, поэтому необходимо учитывать ОДЗ:
. В отличие от уравнений, здесь проверкой обойтись не удастся, поэтому необходимо учитывать ОДЗ: ![]() .
.
Объединяя, получаем: ![]() .
.
![]()
Для ![]() график логарифмической функции выглядит следующим образом:
график логарифмической функции выглядит следующим образом:

![]() - убывающая функция: чем больше
- убывающая функция: чем больше ![]() , тем меньше
, тем меньше ![]() . Значит,
. Значит, ![]() .
.
ОДЗ: ![]() .
.
Объединяя, получаем: ![]()
![]() .
.
Проверка ОДЗ при решении логарифмических неравенств
Лучше всего начинать решение неравенств с проверки ОДЗ. Поскольку даже на первом шаге решения можно получить выражение с измененной ОДЗ.
Например:
![]()
ОДЗ: ![]()
![]()
![]()
А после преобразований: ![]()
ОДЗ: ![]()
|
|
|
|
|
|
![]()
Как быстро определить знак логарифма
Рассмотрим такой полезный факт: как быстро определить знак логарифма?
Рассмотрим два случая:
1) ![]() :
: ![]()
2) ![]() :
: ![]()
Таким образом, ![]() , если
, если ![]() и
и ![]() лежат по одну сторону от 1, и
лежат по одну сторону от 1, и ![]() , если
, если ![]() и
и ![]() лежат по разные стороны от 1.
лежат по разные стороны от 1.
Основные виды логарифмических неравенств
1) Простейшие ![]()
2) Сводящиеся к простейшим ![]()
3) С использованием свойств логарифмов ![]()
4) С заменой ![]()
5) С переменной в основании ![]()
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема: Равносильность систем . Рациональные, иррациональные , показательные системы.
Уравнение, левой и правой частями которого являются числа или многочлены степени не выше первой относительно х и у, называются линейными уравнением с двумя неизвестными х и у.
Члены многочленов, находящиеся в левой и правой частях линейного уравнения, называют членами этого уравнения.
Два уравнения называют равносильными, если любое решение первого уравнения является решением второго, а любое решение второго является решением первого.Равносильны два уравнения, каждое из которых не имеет решения.
Две системы уравнений называют равносильными, если любое решение первой системы является решением второй системы и любое решение второй системы является решением первой системы.
Равносильны две системы, если каждая из них не имеет решений.
Утверждения:
1) Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получим уравнение, равносильное исходному.

2) Если перенести с противоположным знаком член уравнения из одной части в другую, то получим уравнение, равносильное исходному.
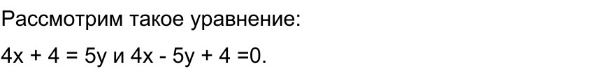
3) Если в левой и правой частях линейного уравнения привести подобные члены, то получится уравнение, равносильное исходному:
![]()
Доказательство этих утверждений проводится так же, как для линейного уравнения с одним неизвестным.


Перенеся свободные члены уравнений этой системы в их правые части, получим следующую равносильную систему:

Пример 2. Решите систему уравнений:

Решите систему уравнений:

Умножим первое уравнение на 2:

План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема Урока: Решение простейших систем уравнений с двумя неизвестными .
Напомним, что любое конечное множество уравнений называется системой уравнений.
Систему уравнений принято записывать с помощью фигурной скобки.
Общий вид системы двух уравнений с двумя переменными:
![]()
Решением системы двух уравнений с двумя переменными называется пара чисел ![]() , при подстановке которых вместо соответствующих переменных
, при подстановке которых вместо соответствующих переменных ![]() оба уравнения системы обращаются в верные числовые равенства.
оба уравнения системы обращаются в верные числовые равенства.
Решить систему уравнений – значит найти все её решения или доказать, что решений нет.
Две системы уравнений называются равносильными, если они имеют одно и то же множество решений. Если обе системы не имеют решений, то они также считаются равносильными.
Теоремы о равносильности систем уравнений.
1. Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а второе уравнение заменить равносильным, то полученная система будет равносильна заданной.
2. Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а второе заменить суммой или разностью обоих уравнений системы, то полученная система будет равносильна заданной.
3. Если обе части уравнения ![]() ни при каких
ни при каких ![]() ,
, ![]() одновременно не обращаются в нуль, то следующие системы равносильны:
одновременно не обращаются в нуль, то следующие системы равносильны:
![]()

Вспомним основные методы решения систем уравнений. Итак, основными методами решения систем уравнений являются метод алгебраического сложения, метод подстановки и метод введения новых переменных.
Метод алгебраического сложения. Сущность этого метода заключается в следующем:
1. обе части первого уравнения умножают на некоторый множитель, обе части второго уравнения умножают на другой множитель (если это требуется). Эти множители подбираются так, чтобы коэффициенты при одной из переменных в обоих уравнениях стали противоположными числами;
2. уравнения почленно складывают и решают полученное уравнение с одной переменной;
3. вторую переменную находят подстановкой найденного значения первой переменной в одно из уравнений системы.
Решите систему уравнений ![]() .
.
Решение.
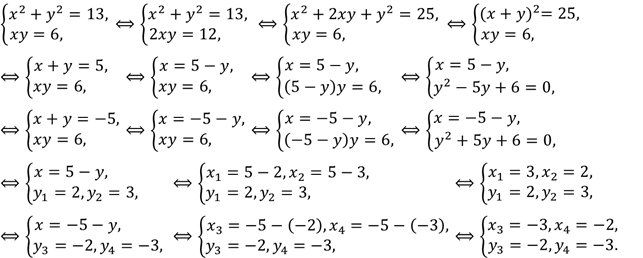
![]()
Решите систему уравнений ![]() .
.
Решение.
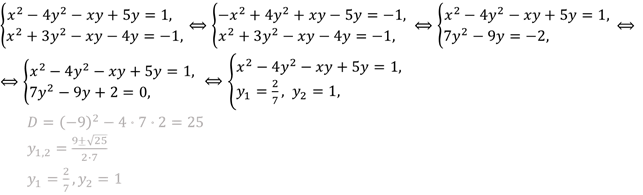

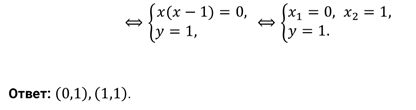
Метод подстановки. Сущность этого метода заключается в следующем:
1) выражают из какого-либо уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующие значения второй переменной.
Решите систему уравнений 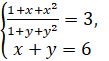 .
.
Решение.
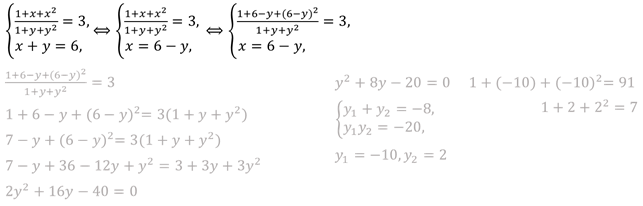
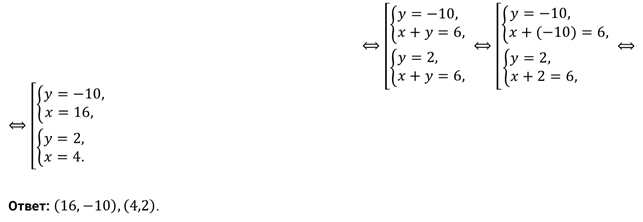
Решите систему уравнений ![]() .
.
Решение.
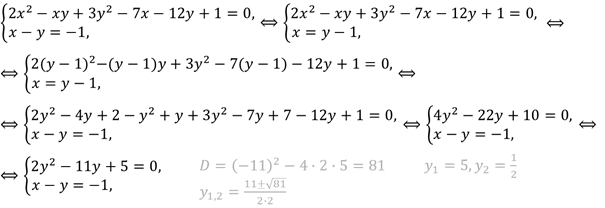

Решите систему уравнений ![]() .
.
Решение.