План урока
Предмет: алгебра
Преподаватель: Амирханова А. К.
Дата проведения:____________
Тема урока: Применение производной для нахождения наибольших и наименьших значений величин
Цель: рассмотреть наибольшее и наименьшее значения функции.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Исследуйте функцию f(х) = sin2 x - sin x и постройте ее график.
2. Сколько корней имеет уравнение 2x4 - 4х3 - 3 = 0?
Вариант 2
1. Исследуйте функцию f(x) = cos2 х + cos x и постройте ее график.
2. Сколько корней имеет уравнение 3х4 - 4х3 - 5 = 0?
III. Изучение нового материала
На прошлом занятии мы научились находить экстремумы - минимумы и максимумы функции. На этом занятии надо рассмотреть применение производной для нахождения наибольших и наименьших значений величин.
1. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
Во многих математических моделях, описывающих реальные ситуации, исследуется поведение функции на заданном отрезке. В частности, нередко возникает задача нахождения наибольшего и наименьшего значений функции.
Пусть функция у = f(x) непрерывна на отрезке [а; b]. Тогда справедливы следующие теоремы (о которых интуитивно мы уже догадывались):
Теорема 1. Функция достигает на отрезке и своего наибольшего, и своего наименьшего значений.
Теорема 2. Наибольшего и наименьшего значений функция может достигать как на концах отрезка, так и внутри его.
Теорема 3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
Учитывая эти теоремы, можно предложить алгоритм нахождения наименьшего и наибольшего значений непрерывной функции у = f(x) на отрезке [а; b]:
1. Найти производную f'(x) функции.
2. Найти стационарные и критические точки, расположенные внутри отрезка [а; b].
3. Вычислить значения функции у = f(x) в стационарных и критических точках, а также на концах отрезка [а; b].
4. Выбрать из этих значений наименьшее yнаим и наибольшее yнаиб.
Пример 1
Найдем наибольшее и наименьшее значения функции f(x) = 18х2 + 8х3 - 3х4 на отрезке [-2; 4].
Вычислим производную данной функции: f'(x) = 36x + 24х2 – 12x3 = 12x(3 + 2x - x2). Приравняем производную нулю, получим уравнение x(3 + 2х - х2) = 0 и найдем стационарные точки функции х1 = 0, x2 = -1 и x3 = 3. Отметим эти точки на координатной оси и построим диаграмму знаков производной f(x). Видно, что в точках x = -1 и х = 3 функция имеет максимум, в точке x = 0 функция имеет минимум. На промежутке [-2; 4] находятся все три точки экстремума.
Вычислим значения функции f(x) в точках экстремума и на концах промежутка. Эти величины приведены в таблице.
|
x
|
-2
|
-1
|
0
|
3
|
4
|
|
f(x)
|
-40
|
7
|
0
|
135
|
32
|
Из сравнения значений функции видно, что унаиб = f(3) = 135 и yнаим = f(-2) = -40. В данном случае наибольшее значение функции достигается в точке максимума х = 3, наименьшее значение - на левой границе х = -2 рассматриваемого промежутка.
Пример 2
Найдем множество значений функции f(x) = 1/2 cos 2х + sin х на отрезке [0; π].
Вычислим производную данной функции: 
 Приравняем производную нулю. Получим уравнение cos х(-2sin х +1) = 0. Произведение множителей равно нулю, если один из них равен нулю. Имеем уравнения cos х = 0 и sin x = 1/2. Их решения на данном отрезке: π/2; π/6; 5π/6. Определим знак производной f’(x), например, при х = 0. Получим:
Приравняем производную нулю. Получим уравнение cos х(-2sin х +1) = 0. Произведение множителей равно нулю, если один из них равен нулю. Имеем уравнения cos х = 0 и sin x = 1/2. Их решения на данном отрезке: π/2; π/6; 5π/6. Определим знак производной f’(x), например, при х = 0. Получим:  Теперь легко построить диаграмму знаков производной. Видно, что в точках х = π/6 и х = 5π/6 функция f(х) имеет максимум, в точке х = π/2 - минимум. Вычислим значения функции f(х) в точках экстремума и на концах отрезка. Эти величины приведены в таблице.
Теперь легко построить диаграмму знаков производной. Видно, что в точках х = π/6 и х = 5π/6 функция f(х) имеет максимум, в точке х = π/2 - минимум. Вычислим значения функции f(х) в точках экстремума и на концах отрезка. Эти величины приведены в таблице.
|
x
|
0
|
π/6
|
π/2
|
5π/6
|
π
|
|
f(х)
|
1/2
|
3/4
|
1/2
|
3/4
|
1/2
|
Из сравнения значений функции видно, что множество значений функции на данном промежутке  Видно, что наименьшее значение достигается в точке минимума и на концах данного отрезка, наибольшее значение - в точках максимума, т. е.
Видно, что наименьшее значение достигается в точке минимума и на концах данного отрезка, наибольшее значение - в точках максимума, т. е. 
Пример 3
Найдем наибольшее значение функции f(x) = 3 + 2ах - х2 на отрезке [1; 2].
Вычислим производную функции: f’(х) = 2а - 2х. Стационарная точка функции х = а. Рассмотрим различное расположение точки а по отношению к данному промежутку [1; 2]. Имеем три случая.

а) Если а ∈ (-∞; 1), то производная f’(x) < 0 на отрезке [1; 2]. Поэтому функция f(x) убывает и достигает наибольшего значения на левой границе промежутка х = 1. Наибольшее значение функции унаиб = f(1) = 2 + 2a.
б) Если а ∈ [1; 2], то стационарная точка находится на данном отрезке и это точка максимума. Тогда наибольшее значение. yнаиб = f(a) = 3 + a2.
в) Если а ∈ (2; ∞), то производная f'(x) > 0 на отрезке [1; 2]. Поэтому функция возрастает и достигает наибольшего значения на правой границе промежутка х = 2. При этом наибольшее значение функции yнаиб = f(2) = 4а - 1.
Итак, при а ∈ (-∞; 1) унаиб = 2 + 2а; при а ∈ [1; 2] унаиб = 3 + а2; при a ∈ (2; ∞)yнаим = 4а - 1.
Пример 4
Криволинейная трапеция ограничена кривой f(х) = х2 + 1, где x ∈ [1; 2], и отрезками прямых х = 1, х = 2, у = 0. В какой точке данной кривой надо провести касательную, чтобы она отсекала от криволинейной трапеции обычную трапецию наибольшей площади?

Предположим, что касательная к графику функции f(х) проведена в точке с абсциссой а. Уравнение этой касательной у = 2а(х - а) + а2 + 1 или y = 2ax + 1 – a2. Найдем площадь трапеции ABCD. Основание АВ = y(1) = 2а + 1 - а2, основание CD = у(2) = 4а + 1 - а2, высота AD = 1. Площадь трапеции 
Найдем производную этой функции: S'(a) = -2а + 3. Стационарная точка функции а = 3/2 принадлежит промежутку [1; 2]. В этой точке функция достигает максимума:  Найдем также значения функции S(a) на концах промежутка: S(1) = 3 и S(2) = 3. Видно, что
Найдем также значения функции S(a) на концах промежутка: S(1) = 3 и S(2) = 3. Видно, что  Таким образом, касательную надо проводить через точку
Таким образом, касательную надо проводить через точку
Обсудим теперь нахождение наименьшего и наибольшего значений функции на промежутке X. В этом случае полезна следующая теорема.
Теорема 4. Пусть функция у = f(х) непрерывна на промежутке X и имеет внутри его единственную стационарную или критическую точку х = x0. Тогда:
а) если х = х0 - точка максимума, то yнаиб = f(x0);
б) если х = х0 - точка минимума, то yнаим = f(х0).
Пример 5
Найдем наибольшее и наименьшее значения функции  на луче [0; +∞).
на луче [0; +∞).
Найдем производную функции: 
 Производная существует при всех значениях х, и функция критических точек не имеет. Стационарные точки находим из условия f’(x) = 0 и получим x = ±1. На рассматриваемом промежутке находится единственная стационарная точка х = 1. При х < 1 f'(x) < 0, при х > 1 f'(x) > 0. Следовательно, х = 1 - точка минимума и
Производная существует при всех значениях х, и функция критических точек не имеет. Стационарные точки находим из условия f’(x) = 0 и получим x = ±1. На рассматриваемом промежутке находится единственная стационарная точка х = 1. При х < 1 f'(x) < 0, при х > 1 f'(x) > 0. Следовательно, х = 1 - точка минимума и 
Так как х = 1 - единственная стационарная точка на промежутке [0; +∞), то по теореме 4 унаим = ymin = 2/3. При х = 0 (на конце промежутка) у(0) = 1/1 = 1. График функции имеет горизонтальную асимптоту у = 1. Тогда yнаиб = у(0) = 1. Для наглядности приведен график этой функции.

2. Задачи на нахождение наибольших и наименьших значений величин
На практике часто встречаются задачи на оптимизацию (наименьшие затраты на производство, наименьшее время движения, наибольшая прибыль при сбыте продукции и т. д.).
Рассмотрим типичную задачу из этого раздела, а потом сформулируем алгоритм решения подобных задач.
Пример 6
Участок расположен на границе дачного поселка, с одной стороны уже огражден и должен иметь прямоугольную форму. Как оградить участок с остальных трех сторон, чтобы его площадь была наибольшей, а длина забора составляла а м?
Видно, что имеем типичную задачу на оптимизацию - при фиксированных затратах (длина забора) надо получить максимальную прибыль (площадь участка).

Пусть АВ - общий забор дачного поселка, CDEF - участок. Необходимо оградить стороны CD, DE, EF. Обозначим длину сторон CD и EF буквой х, длину стороны DE - у. Тогда площадь участка S = CD · DE = ху. Необходимо, чтобы величина S = ху была наибольшей. Но S зависит от двух переменных х и у. Поэтому надо найти связь между этими переменными. Для этого используем условие задачи - длина забора равна а, т. е.CD + DE + EF = а или х + у + х = а, откуда у = а - 2х.
Тогда S = ху = х(а - 2х) = -2х2 + ах. Необходимо, чтобы эта величина была наибольшей. Вообще-то, функция S(x) является квадратичной, и для ее исследования производная не нужна. Тем не менее, чтобы не нарушать общности подхода, мы ее используем.
Найдем производную функции S(х) = -2х2 + ах и получим: S'(x) = -4х + а. Функция имеет единственную стационарную точку х0 = a/4. Легко показать, что это точка максимума. Действительно, S’(0) = а > 0, S'(а) = -3а < 0, т. е. производная меняет знак с плюса на минус. Найдем значение переменной: 
Видим, что у0 = 2х0. Поэтому участок надо ограждать так, чтобы одна его сторона была вдвое больше другой. При этом наибольшая площадь 
Таким образом, были получены ответы на все возникшие вопросы.
Теперь сформулируем алгоритм оптимизации:
1. Выбрать оптимизируемую величину (S) и переменные (х, у), через которые она выражается.
2. Найти связь между переменными х и у, используя условия задачи.
3. Получить зависимость оптимизируемой величины S от одной переменной, х, т. е. функцию S(x).
4. Провести исследование функции S(x) на наибольшее или наименьшее значения.
Пример 7
Турист идет из пункта А, находящегося на шоссе, в пункт В, расположенный в 8 км от шоссе. Расстояние от А до В по прямой равно 17 км. На каком расстоянии от А туристу следует свернуть с шоссе, чтобы в кратчайшее время прийти в пункт В, если его скорость по шоссе равна 5 км/м, а по бездорожью - 3 км/ч?

Пусть АС - шоссе, тогда ВС = 8 и АВ = 17. Пусть турист свернул в точке D. Обозначим расстояния АВ = х и DB = у. Время движения туриста 
Найдем связь между переменными х и у. Из прямоугольного треугольника ABC по теореме Пифагора найдем: 
 Из прямоугольного треугольникаBCD получим:
Из прямоугольного треугольникаBCD получим:  Очевидно, что AD + DC = АС или
Очевидно, что AD + DC = АС или  Проще всего из этого равенства выразить
Проще всего из этого равенства выразить 
Запишем время движения туриста: 
 Получили зависимость оптимизируемой величины t от переменной у, т. е. функцию t(y).
Получили зависимость оптимизируемой величины t от переменной у, т. е. функцию t(y).
Найдем производную функции  и получим:
и получим:  На рисунке видно, что 8 ≤ у ≤ 17. Поэтому критическая точка функции t(y) равна 8 (производная не существует). При этом
На рисунке видно, что 8 ≤ у ≤ 17. Поэтому критическая точка функции t(y) равна 8 (производная не существует). При этом 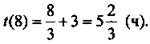
Стационарная точка определяется условием t'(у) = 0, т. е.  или
или  Возведем в квадрат обе части этого иррационального уравнения: 25у2 - 1600 = 9у2, откуда y2 = 100 и у = 10. Можно проверить, что это точка минимума и
Возведем в квадрат обе части этого иррационального уравнения: 25у2 - 1600 = 9у2, откуда y2 = 100 и у = 10. Можно проверить, что это точка минимума и 

Найдем также значение функции на границе промежутка:  Сравнивая значения функции в точке минимума
Сравнивая значения функции в точке минимума  и на концах промежутка
и на концах промежутка  получим наименьшее значение функции
получим наименьшее значение функции 
Найдем переменную:  Таким образом, сворачивать с шоссе надо в 9 км от пункта А.
Таким образом, сворачивать с шоссе надо в 9 км от пункта А.
IV. Контрольные вопросы
1. Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции на отрезке.
2. Алгоритм оптимизации функции.
V. Задание на уроках
§ 32, № 1 (а, б); 2 (в, г); 8; 13 (а, б); 15 (в, г); 16 (а); 17 (б); 18 (а); 23; 25; 26; 30; 32; 37 (а); 38 (б).
VI. Задание на дом
§ 32, № 1 (в, г); 2 (а, б); 9; 13 (в, г); 15 (а, б); 16 (б); 17 (а); 18 (б); 24; 27; 28; 31; 33; 37 (б); 38 (а).
VII. Подведение итогов уроков
Просмотр содержимого документа
«Тема урока: Применение производной для нахождения наибольших и наименьших значений величин»
План урока
Предмет: алгебра
Преподаватель: Амирханова А. К.
Дата проведения:____________
Тема урока: Применение производной для нахождения наибольших и наименьших значений величин
Цель: рассмотреть наибольшее и наименьшее значения функции.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Исследуйте функцию f(х) = sin2 x - sin x и постройте ее график.
2. Сколько корней имеет уравнение 2x4 - 4х3 - 3 = 0?
Вариант 2
1. Исследуйте функцию f(x) = cos2 х + cos x и постройте ее график.
2. Сколько корней имеет уравнение 3х4 - 4х3 - 5 = 0?
III. Изучение нового материала
На прошлом занятии мы научились находить экстремумы - минимумы и максимумы функции. На этом занятии надо рассмотреть применение производной для нахождения наибольших и наименьших значений величин.
1. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
Во многих математических моделях, описывающих реальные ситуации, исследуется поведение функции на заданном отрезке. В частности, нередко возникает задача нахождения наибольшего и наименьшего значений функции.
Пусть функция у = f(x) непрерывна на отрезке [а; b]. Тогда справедливы следующие теоремы (о которых интуитивно мы уже догадывались):
Теорема 1. Функция достигает на отрезке и своего наибольшего, и своего наименьшего значений.
Теорема 2. Наибольшего и наименьшего значений функция может достигать как на концах отрезка, так и внутри его.
Теорема 3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
Учитывая эти теоремы, можно предложить алгоритм нахождения наименьшего и наибольшего значений непрерывной функции у = f(x) на отрезке [а; b]:
1. Найти производную f'(x) функции.
2. Найти стационарные и критические точки, расположенные внутри отрезка [а; b].
3. Вычислить значения функции у = f(x) в стационарных и критических точках, а также на концах отрезка [а; b].
4. Выбрать из этих значений наименьшее yнаим и наибольшее yнаиб.
Пример 1
Найдем наибольшее и наименьшее значения функции f(x) = 18х2 + 8х3 - 3х4 на отрезке [-2; 4].
Вычислим производную данной функции: f'(x) = 36x + 24х2 – 12x3 = 12x(3 + 2x - x2). Приравняем производную нулю, получим уравнение x(3 + 2х - х2) = 0 и найдем стационарные точки функции х1 = 0, x2 = -1 и x3 = 3. Отметим эти точки на координатной оси и построим диаграмму знаков производной f(x). Видно, что в точках x = -1 и х = 3 функция имеет максимум, в точке x = 0 функция имеет минимум. На промежутке [-2; 4] находятся все три точки экстремума.
Вычислим значения функции f(x) в точках экстремума и на концах промежутка. Эти величины приведены в таблице.
| x | -2 | -1 | 0 | 3 | 4 |
| f(x) | -40 | 7 | 0 | 135 | 32 |
Из сравнения значений функции видно, что унаиб = f(3) = 135 и yнаим = f(-2) = -40. В данном случае наибольшее значение функции достигается в точке максимума х = 3, наименьшее значение - на левой границе х = -2 рассматриваемого промежутка.
Пример 2
Найдем множество значений функции f(x) = 1/2 cos 2х + sin х на отрезке [0; π].
Вычислим производную данной функции: 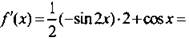
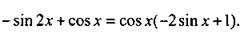 Приравняем производную нулю. Получим уравнение cos х(-2sin х +1) = 0. Произведение множителей равно нулю, если один из них равен нулю. Имеем уравнения cos х = 0 и sin x = 1/2. Их решения на данном отрезке: π/2; π/6; 5π/6. Определим знак производной f’(x), например, при х = 0. Получим:
Приравняем производную нулю. Получим уравнение cos х(-2sin х +1) = 0. Произведение множителей равно нулю, если один из них равен нулю. Имеем уравнения cos х = 0 и sin x = 1/2. Их решения на данном отрезке: π/2; π/6; 5π/6. Определим знак производной f’(x), например, при х = 0. Получим:  Теперь легко построить диаграмму знаков производной. Видно, что в точках х = π/6 и х = 5π/6 функция f(х) имеет максимум, в точке х = π/2 - минимум. Вычислим значения функции f(х) в точках экстремума и на концах отрезка. Эти величины приведены в таблице.
Теперь легко построить диаграмму знаков производной. Видно, что в точках х = π/6 и х = 5π/6 функция f(х) имеет максимум, в точке х = π/2 - минимум. Вычислим значения функции f(х) в точках экстремума и на концах отрезка. Эти величины приведены в таблице.
| x | 0 | π/6 | π/2 | 5π/6 | π |
| f(х) | 1/2 | 3/4 | 1/2 | 3/4 | 1/2 |
Из сравнения значений функции видно, что множество значений функции на данном промежутке 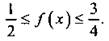 Видно, что наименьшее значение достигается в точке минимума и на концах данного отрезка, наибольшее значение - в точках максимума, т. е.
Видно, что наименьшее значение достигается в точке минимума и на концах данного отрезка, наибольшее значение - в точках максимума, т. е. 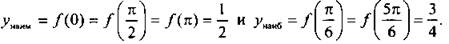
Пример 3
Найдем наибольшее значение функции f(x) = 3 + 2ах - х2 на отрезке [1; 2].
Вычислим производную функции: f’(х) = 2а - 2х. Стационарная точка функции х = а. Рассмотрим различное расположение точки а по отношению к данному промежутку [1; 2]. Имеем три случая.

а) Если а ∈ (-∞; 1), то производная f’(x) f(x) убывает и достигает наибольшего значения на левой границе промежутка х = 1. Наибольшее значение функции унаиб = f(1) = 2 + 2a.
б) Если а ∈ [1; 2], то стационарная точка находится на данном отрезке и это точка максимума. Тогда наибольшее значение. yнаиб = f(a) = 3 + a2.
в) Если а ∈ (2; ∞), то производная f'(x) 0 на отрезке [1; 2]. Поэтому функция возрастает и достигает наибольшего значения на правой границе промежутка х = 2. При этом наибольшее значение функции yнаиб = f(2) = 4а - 1.
Итак, при а ∈ (-∞; 1) унаиб = 2 + 2а; при а ∈ [1; 2] унаиб = 3 + а2; при a ∈ (2; ∞)yнаим = 4а - 1.
Пример 4
Криволинейная трапеция ограничена кривой f(х) = х2 + 1, где x ∈ [1; 2], и отрезками прямых х = 1, х = 2, у = 0. В какой точке данной кривой надо провести касательную, чтобы она отсекала от криволинейной трапеции обычную трапецию наибольшей площади?
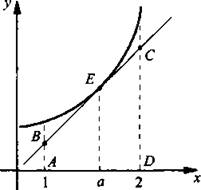
Предположим, что касательная к графику функции f(х) проведена в точке с абсциссой а. Уравнение этой касательной у = 2а(х - а) + а2 + 1 или y = 2ax + 1 – a2. Найдем площадь трапеции ABCD. Основание АВ = y(1) = 2а + 1 - а2, основание CD = у(2) = 4а + 1 - а2, высота AD = 1. Площадь трапеции 
Найдем производную этой функции: S'(a) = -2а + 3. Стационарная точка функции а = 3/2 принадлежит промежутку [1; 2]. В этой точке функция достигает максимума:  Найдем также значения функции S(a) на концах промежутка: S(1) = 3 и S(2) = 3. Видно, что
Найдем также значения функции S(a) на концах промежутка: S(1) = 3 и S(2) = 3. Видно, что  Таким образом, касательную надо проводить через точку
Таким образом, касательную надо проводить через точку
Обсудим теперь нахождение наименьшего и наибольшего значений функции на промежутке X. В этом случае полезна следующая теорема.
Теорема 4. Пусть функция у = f(х) непрерывна на промежутке X и имеет внутри его единственную стационарную или критическую точку х = x0. Тогда:
а) если х = х0 - точка максимума, то yнаиб = f(x0);
б) если х = х0 - точка минимума, то yнаим = f(х0).
Пример 5
Найдем наибольшее и наименьшее значения функции 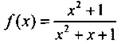 на луче [0; +∞).
на луче [0; +∞).
Найдем производную функции: 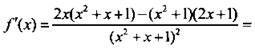
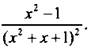 Производная существует при всех значениях х, и функция критических точек не имеет. Стационарные точки находим из условия f’(x) = 0 и получим x = ±1. На рассматриваемом промежутке находится единственная стационарная точка х = 1. При х f'(x) 1 f'(x) 0. Следовательно, х = 1 - точка минимума и
Производная существует при всех значениях х, и функция критических точек не имеет. Стационарные точки находим из условия f’(x) = 0 и получим x = ±1. На рассматриваемом промежутке находится единственная стационарная точка х = 1. При х f'(x) 1 f'(x) 0. Следовательно, х = 1 - точка минимума и 
Так как х = 1 - единственная стационарная точка на промежутке [0; +∞), то по теореме 4 унаим = ymin = 2/3. При х = 0 (на конце промежутка) у(0) = 1/1 = 1. График функции имеет горизонтальную асимптоту у = 1. Тогда yнаиб = у(0) = 1. Для наглядности приведен график этой функции.

2. Задачи на нахождение наибольших и наименьших значений величин
На практике часто встречаются задачи на оптимизацию (наименьшие затраты на производство, наименьшее время движения, наибольшая прибыль при сбыте продукции и т. д.).
Рассмотрим типичную задачу из этого раздела, а потом сформулируем алгоритм решения подобных задач.
Пример 6
Участок расположен на границе дачного поселка, с одной стороны уже огражден и должен иметь прямоугольную форму. Как оградить участок с остальных трех сторон, чтобы его площадь была наибольшей, а длина забора составляла а м?
Видно, что имеем типичную задачу на оптимизацию - при фиксированных затратах (длина забора) надо получить максимальную прибыль (площадь участка).

Пусть АВ - общий забор дачного поселка, CDEF - участок. Необходимо оградить стороны CD, DE, EF. Обозначим длину сторон CD и EF буквой х, длину стороны DE - у. Тогда площадь участка S = CD · DE = ху. Необходимо, чтобы величина S = ху была наибольшей. Но S зависит от двух переменных х и у. Поэтому надо найти связь между этими переменными. Для этого используем условие задачи - длина забора равна а, т. е.CD + DE + EF = а или х + у + х = а, откуда у = а - 2х.
Тогда S = ху = х(а - 2х) = -2х2 + ах. Необходимо, чтобы эта величина была наибольшей. Вообще-то, функция S(x) является квадратичной, и для ее исследования производная не нужна. Тем не менее, чтобы не нарушать общности подхода, мы ее используем.
Найдем производную функции S(х) = -2х2 + ах и получим: S'(x) = -4х + а. Функция имеет единственную стационарную точку х0 = a/4. Легко показать, что это точка максимума. Действительно, S’(0) = а 0, S'(а) = -3а 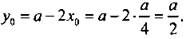
Видим, что у0 = 2х0. Поэтому участок надо ограждать так, чтобы одна его сторона была вдвое больше другой. При этом наибольшая площадь 
Таким образом, были получены ответы на все возникшие вопросы.
Теперь сформулируем алгоритм оптимизации:
1. Выбрать оптимизируемую величину (S) и переменные (х, у), через которые она выражается.
2. Найти связь между переменными х и у, используя условия задачи.
3. Получить зависимость оптимизируемой величины S от одной переменной, х, т. е. функцию S(x).
4. Провести исследование функции S(x) на наибольшее или наименьшее значения.
Пример 7
Турист идет из пункта А, находящегося на шоссе, в пункт В, расположенный в 8 км от шоссе. Расстояние от А до В по прямой равно 17 км. На каком расстоянии от А туристу следует свернуть с шоссе, чтобы в кратчайшее время прийти в пункт В, если его скорость по шоссе равна 5 км/м, а по бездорожью - 3 км/ч?
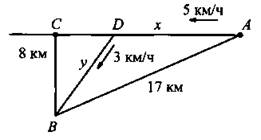
Пусть АС - шоссе, тогда ВС = 8 и АВ = 17. Пусть турист свернул в точке D. Обозначим расстояния АВ = х и DB = у. Время движения туриста 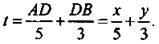
Найдем связь между переменными х и у. Из прямоугольного треугольника ABC по теореме Пифагора найдем: 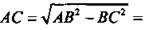
 Из прямоугольного треугольникаBCD получим:
Из прямоугольного треугольникаBCD получим: 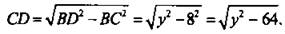 Очевидно, что AD + DC = АС или
Очевидно, что AD + DC = АС или 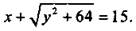 Проще всего из этого равенства выразить
Проще всего из этого равенства выразить 
Запишем время движения туриста: 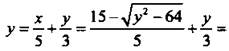
 Получили зависимость оптимизируемой величины t от переменной у, т. е. функцию t(y).
Получили зависимость оптимизируемой величины t от переменной у, т. е. функцию t(y).
Найдем производную функции 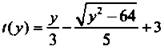 и получим:
и получим: 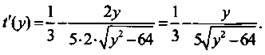 На рисунке видно, что 8 ≤ у ≤ 17. Поэтому критическая точка функции t(y) равна 8 (производная не существует). При этом
На рисунке видно, что 8 ≤ у ≤ 17. Поэтому критическая точка функции t(y) равна 8 (производная не существует). При этом 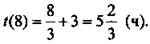
Стационарная точка определяется условием t'(у) = 0, т. е.  или
или  Возведем в квадрат обе части этого иррационального уравнения: 25у2 - 1600 = 9у2, откуда y2 = 100 и у = 10. Можно проверить, что это точка минимума и
Возведем в квадрат обе части этого иррационального уравнения: 25у2 - 1600 = 9у2, откуда y2 = 100 и у = 10. Можно проверить, что это точка минимума и 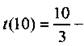
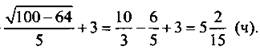
Найдем также значение функции на границе промежутка: 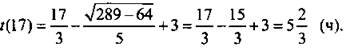 Сравнивая значения функции в точке минимума
Сравнивая значения функции в точке минимума  и на концах промежутка
и на концах промежутка 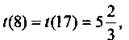 получим наименьшее значение функции
получим наименьшее значение функции 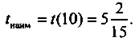
Найдем переменную:  Таким образом, сворачивать с шоссе надо в 9 км от пункта А.
Таким образом, сворачивать с шоссе надо в 9 км от пункта А.
IV. Контрольные вопросы
1. Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции на отрезке.
2. Алгоритм оптимизации функции.
V. Задание на уроках
§ 32, № 1 (а, б); 2 (в, г); 8; 13 (а, б); 15 (в, г); 16 (а); 17 (б); 18 (а); 23; 25; 26; 30; 32; 37 (а); 38 (б).
VI. Задание на дом
§ 32, № 1 (в, г); 2 (а, б); 9; 13 (в, г); 15 (а, б); 16 (б); 17 (а); 18 (б); 24; 27; 28; 31; 33; 37 (б); 38 (а).
VII. Подведение итогов уроков







 Приравняем производную нулю. Получим уравнение cos х(-2sin х +1) = 0. Произведение множителей равно нулю, если один из них равен нулю. Имеем уравнения cos х = 0 и sin x = 1/2. Их решения на данном отрезке: π/2; π/6; 5π/6. Определим знак производной f’(x), например, при х = 0. Получим:
Приравняем производную нулю. Получим уравнение cos х(-2sin х +1) = 0. Произведение множителей равно нулю, если один из них равен нулю. Имеем уравнения cos х = 0 и sin x = 1/2. Их решения на данном отрезке: π/2; π/6; 5π/6. Определим знак производной f’(x), например, при х = 0. Получим:  Теперь легко построить диаграмму знаков производной. Видно, что в точках х = π/6 и х = 5π/6 функция f(х) имеет максимум, в точке х = π/2 - минимум. Вычислим значения функции f(х) в точках экстремума и на концах отрезка. Эти величины приведены в таблице.
Теперь легко построить диаграмму знаков производной. Видно, что в точках х = π/6 и х = 5π/6 функция f(х) имеет максимум, в точке х = π/2 - минимум. Вычислим значения функции f(х) в точках экстремума и на концах отрезка. Эти величины приведены в таблице. Видно, что наименьшее значение достигается в точке минимума и на концах данного отрезка, наибольшее значение - в точках максимума, т. е.
Видно, что наименьшее значение достигается в точке минимума и на концах данного отрезка, наибольшее значение - в точках максимума, т. е. 



 Найдем также значения функции S(a) на концах промежутка: S(1) = 3 и S(2) = 3. Видно, что
Найдем также значения функции S(a) на концах промежутка: S(1) = 3 и S(2) = 3. Видно, что  Таким образом, касательную надо проводить через точку
Таким образом, касательную надо проводить через точку
 на луче [0; +∞).
на луче [0; +∞).
 Производная существует при всех значениях х, и функция критических точек не имеет. Стационарные точки находим из условия f’(x) = 0 и получим x = ±1. На рассматриваемом промежутке находится единственная стационарная точка х = 1. При х < 1 f'(x) < 0, при х > 1 f'(x) > 0. Следовательно, х = 1 - точка минимума и
Производная существует при всех значениях х, и функция критических точек не имеет. Стационарные точки находим из условия f’(x) = 0 и получим x = ±1. На рассматриваемом промежутке находится единственная стационарная точка х = 1. При х < 1 f'(x) < 0, при х > 1 f'(x) > 0. Следовательно, х = 1 - точка минимума и 







 Из прямоугольного треугольникаBCD получим:
Из прямоугольного треугольникаBCD получим:  Очевидно, что AD + DC = АС или
Очевидно, что AD + DC = АС или  Проще всего из этого равенства выразить
Проще всего из этого равенства выразить 

 Получили зависимость оптимизируемой величины t от переменной у, т. е. функцию t(y).
Получили зависимость оптимизируемой величины t от переменной у, т. е. функцию t(y). и получим:
и получим:  На рисунке видно, что 8 ≤ у ≤ 17. Поэтому критическая точка функции t(y) равна 8 (производная не существует). При этом
На рисунке видно, что 8 ≤ у ≤ 17. Поэтому критическая точка функции t(y) равна 8 (производная не существует). При этом 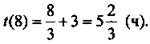
 или
или  Возведем в квадрат обе части этого иррационального уравнения: 25у2 - 1600 = 9у2, откуда y2 = 100 и у = 10. Можно проверить, что это точка минимума и
Возведем в квадрат обе части этого иррационального уравнения: 25у2 - 1600 = 9у2, откуда y2 = 100 и у = 10. Можно проверить, что это точка минимума и 

 Сравнивая значения функции в точке минимума
Сравнивая значения функции в точке минимума  и на концах промежутка
и на концах промежутка  получим наименьшее значение функции
получим наименьшее значение функции 
 Таким образом, сворачивать с шоссе надо в 9 км от пункта А.
Таким образом, сворачивать с шоссе надо в 9 км от пункта А.
 Найдем также значения функции S(a) на концах промежутка: S(1) = 3 и S(2) = 3. Видно, что
Найдем также значения функции S(a) на концах промежутка: S(1) = 3 и S(2) = 3. Видно, что 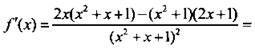
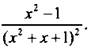 Производная существует при всех значениях х, и функция критических точек не имеет. Стационарные точки находим из условия f’(x) = 0 и получим x = ±1. На рассматриваемом промежутке находится единственная стационарная точка х = 1. При х f'(x) 1 f'(x) 0. Следовательно, х = 1 - точка минимума и
Производная существует при всех значениях х, и функция критических точек не имеет. Стационарные точки находим из условия f’(x) = 0 и получим x = ±1. На рассматриваемом промежутке находится единственная стационарная точка х = 1. При х f'(x) 1 f'(x) 0. Следовательно, х = 1 - точка минимума и 


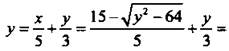
 Получили зависимость оптимизируемой величины t от переменной у, т. е. функцию t(y).
Получили зависимость оптимизируемой величины t от переменной у, т. е. функцию t(y).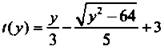 и получим:
и получим: 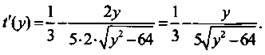 На рисунке видно, что 8 ≤ у ≤ 17. Поэтому критическая точка функции t(y) равна 8 (производная не существует). При этом
На рисунке видно, что 8 ≤ у ≤ 17. Поэтому критическая точка функции t(y) равна 8 (производная не существует). При этом  или
или 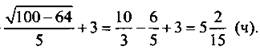
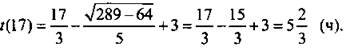 Сравнивая значения функции в точке минимума
Сравнивая значения функции в точке минимума 









