Тема урока: «Теорема синусов. Решение треугольников»
Цели урока: показать применение теоремы косинусов при решении задач;
рассмотреть доказательство теоремы синусов, развивать логическое мышление при решении геометрических задач, пробудить интерес к изучению геометрии.
Ход урока.
I.Оргмомен
Эпиграф
«Вдохновение нужно в геометрии
не меньше, чем в поэзии»
(А.С. Пушкин)
II. Проверка усвоения ранее пройденного материала
Примените теорему косинусов к прямоугольному треугольнику. Что получилось?
c2 =a2 +b2 + 2ab cosɤ, так как ɤ=90˚, то cos 90˚=0
c2 =a2 +b2 +0
c2 =a2 +b2 – теорема Пифагора
2.Объясните постановку знаков «±» в теореме косинусов.
Если угол противолежащий стороне острый, то 2ab cosɤ отнимают, а если угол тупой, то 2ab cos ɤ прибавляют.
cos (180˚-α)= - cos α
c2 =a2 +b2 -2ab cos (180˚-α) = c2 =a2 +b2 -2ab(-cos α) = a2 +b2 +2ab cos ɤ.
Если градусная мера угла больше 90˚, то в теореме знак минус меняется на плюс.
2. Перед вами различные треугольники. В каких случаях мы сможем применить теорему косинусов и что с помощью нее мы сможем найти?
Учащиеся устно обосновывают свой выбор, записывают формулы вычисления стороны или угла.
Вывод: Для применения теоремы косинусов необходимы следующие данные:
-величины трех сторон;
-две стороны и угол между ними.
В одной задаче нет необходимого набора данных, позволяющих решить задачу. Как же быть в этом случае? (Можно решить задачу с использованием синуса угла, если в треугольнике провести высоту).
III. Работа над новым материалом
Сегодня на уроке нам предстоит познакомиться еще с одной теоремой, применение которой возможно при решении задач, в которых необходимо найти стороны или углы треугольника.
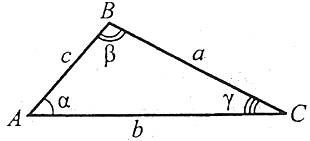
1.Теорема (синусов):
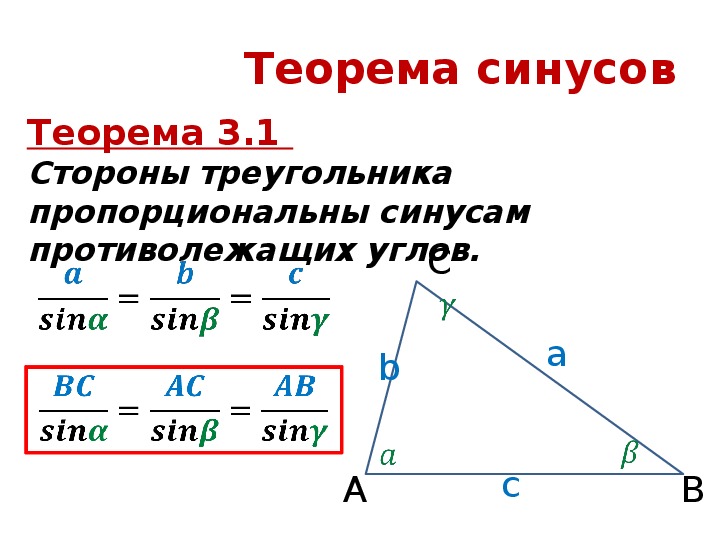
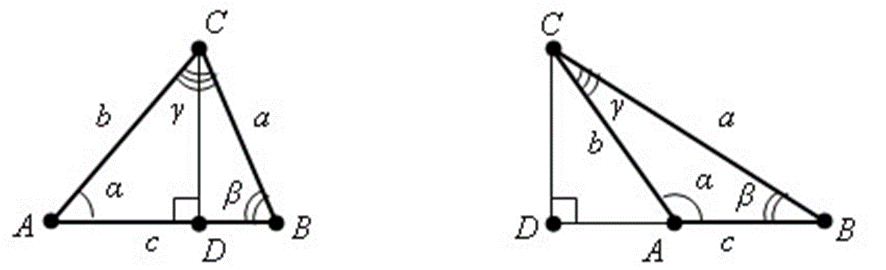
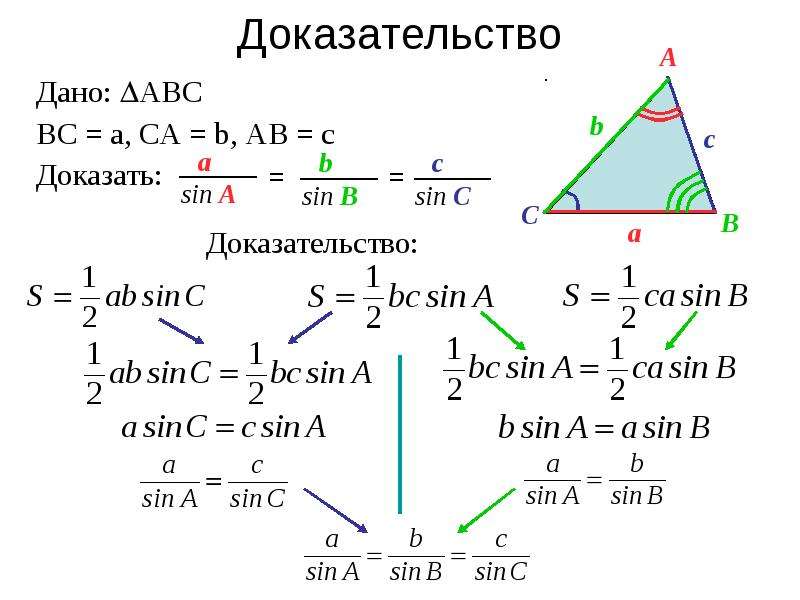
Как вы думаете, что лежит в основе доказательства данной теоремы?
Как находится синус острого угла в прямоугольном треугольнике?
sin α= 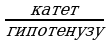 (противолежащий)
(противолежащий)
Давайте данную теорему рассмотрим иначе, как интересную сказку. Ведь не забывайте:
«Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение».
(В. Произволов)
Прежде чем начать нашу историю, необходимо еле заметными линиями начертить остроугольный треугольник и обозначить все стороны и углы (чтобы избежать дальнейшей буквенной путаницы). Наша история начинается:
Жил-был катет. Хорошо жил, так как у него был обогреватель марки «sinɤ», который обогревал его от пяток до головы. Особенно катету нравился самый длинный тепловой лучик, который ласково гладил его по голове, согревал голову . Он даже имя ему дал «а». И так у катета вся жизнь была связана с лучиком и обогревателем.
Катет = а∙ sinɤ
Однажды катет задумался: «А нельзя ли еще приобрести себе обогреватель? А то нос мерзнет». Купил он новый обогреватель марки «sin α», подключил его и не нарадуется. Теперь самый длинный лучик ему и нос согрел, а в благодарность лучик получил имя «с» .
c sin α= Катет = а sinɤ
Ж ивет катет, в лучах обогревателя наслаждается теплом. Обогреватели его не только согрели со всех сторон, а и насквозь всего прогрели . Прошли тепловые лучи сквозь катет и разделили друг друга на части. Так обогреватель марки «sin α» поделил драгоценный лучик «a» на части, а «sinɤ» - поделил «с» С тех пор
ивет катет, в лучах обогревателя наслаждается теплом. Обогреватели его не только согрели со всех сторон, а и насквозь всего прогрели . Прошли тепловые лучи сквозь катет и разделили друг друга на части. Так обогреватель марки «sin α» поделил драгоценный лучик «a» на части, а «sinɤ» - поделил «с» С тех пор 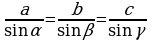
Сказка ложь, да в ней намек, добрым молодцам урок!
Если сложно запомнить трудную информацию, попытайтесь творчески подойти к ее запоминанию, а для этого можно придумать свою увлекательную историю.
IV. Закрепление материала
Давайте рассмотрим, в каких случаях уместно применение теоремы синусов, для этого мы должны знать:
-две стороны и угол, лежащий напротив одной из них;
-два угла и сторону, лежащую напротив одного из них
Решение данной задачи у доски с подробным комментированием
РЭШ урок 15 тренировочные задания.
V. Обобщение
Давайте вспомним, какой путь в познании материала мы проделали, пока достигли теоремы синусов.
VI.Домашнее задание
Теорема синусов с доказательством, составить и решить задачу на использование теоремы синусов
VII. Рефлексия
Оцени качество своих познаний на уроке :
А) Все легко и понятно
Б) Кажется, что-то понял
В) Трудно, ничего не понял
П
 риложение
риложение
а
в
а
- 2ab cosɤ
а)
с
в
с
с
б)
в)
в)

+ 2ab cosɤ
г)
д)
Рис.1
Рис. 2





120˚
В С


6
7
20
75
35
40˚
130˚
В В В
8

60˚

7
23


А
А С А С А С
а) б) в) г)
Рис.3
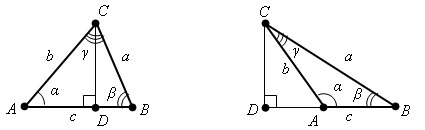
а) б)
Рис.4

а
а
с
sin ɤ
а)
sin ɤ
sin α
б)
в)
а)

г)
с
а
sin ɤ
sin α
Рис.5
Теорема синусов

Таблица В.М. Брадиса

Sin (180˚-α) = sin α

Sin α
прямоугольный треугольник
Рис.6

В
 се легко и понятно
се легко и понятно
Кажется, что-то понял
Трудно, ничего не понял
Рис.7









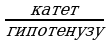 (противолежащий)
(противолежащий)  ивет катет, в лучах обогревателя наслаждается теплом. Обогреватели его не только согрели со всех сторон, а и насквозь всего прогрели . Прошли тепловые лучи сквозь катет и разделили друг друга на части. Так обогреватель марки «sin α» поделил драгоценный лучик «a» на части, а «sinɤ» - поделил «с» С тех пор
ивет катет, в лучах обогревателя наслаждается теплом. Обогреватели его не только согрели со всех сторон, а и насквозь всего прогрели . Прошли тепловые лучи сквозь катет и разделили друг друга на части. Так обогреватель марки «sin α» поделил драгоценный лучик «a» на части, а «sinɤ» - поделил «с» С тех пор 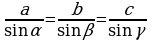


 риложение
риложение



















 се легко и понятно
се легко и понятно 









