ТЕОРЕМЫ МЕНЕЛАЯ И ЧЕВЫ. Примеры решения задач.

ТЕОРЕМЫ МЕНЕЛАЯ И ЧЕВЫ

• РЕШЕНИЕ ЗАДАЧ
• РЕШЕНИЕ ЗАДАЧ
• РЕШЕНИЕ ЗАДАЧ
• РЕШЕНИЕ ЗАДАЧ
• РЕШЕНИЕ ЗАДАЧ
• РЕШЕНИЕ ЗАДАЧ
• РЕШЕНИЕ ЗАДАЧ
• РЕШЕНИЕ ЗАДАЧ
• РЕШЕНИЕ ЗАДАЧ

Выполнила: Борцова Ксения Александровна

Ученица 11 класса

ГОУ ЛНР КСШ №1 им. А.М.Горького

г. Краснодон, 2024 год

СОДЕРЖАНИЕ

4

3

2

5

1

ВВЕДЕНИЕ

ТЕОРИЯ 1

ТЕОРИЯ 2

ПРАКТИКА

ЗАКЛЮЧЕНИЕ

Выводы о провёденной работе

Актуальность

работы

Теорема Менелая, её формулировка и доказательство .

Теорема Чевы, её формулировка и доказательство .

Решение задач с помощью предложенных теорем .

Введение

Теоремы Чевы и Менелая – одни из базовых основ планиметрии и геометрии, которым репетиторы и школьные учителя уделяют особое внимание, а ученикам задают писать научные доклады и рефераты на эту тему в качестве домашнего задания.

  Их изучение рекомендуется не только в том случае, если вы – математик, но и в помощь ученикам старшего уровня (по уровню сложности может подойти и любой средний класс) и студентам профильных специальностей, которые всерьёз интересуются данной наукой.

ТЕОРИЯ 1

Менелай Александрийский (1-2 вв. н.э.)

Греческий математик и астроном.

Теорема Менелая входит в золотой фонд древнегреческой математики. Она дошла до нас в арабском переводе его книги «Сферика».

(Перевод на арабский язык выполнил в начале X века Хунайн ал-Ибади)

Равенство Менелая Александрийского можно записывать, начиная с любой вершины треугольника,в любом направлении (по часовой стрелке, против часовой стрелки ).

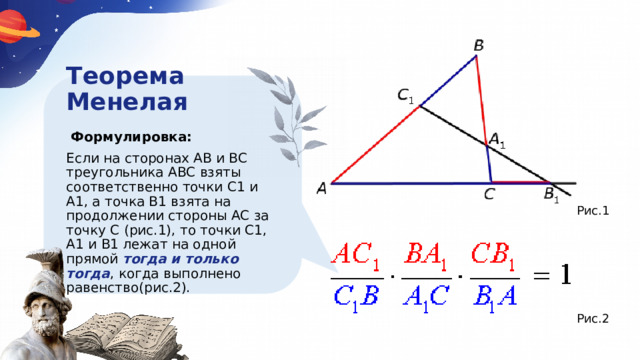
Теорема Менелая

  Формулировка:

Если на сторонах AB и BC треугольника ABC взяты соответственно точки C1 и A1, а точка B1 взята на продолжении стороны AC за точку C (рис.1), то точки C1, A1 и B1 лежат на одной прямой тогда и только тогда , когда выполнено равенство(рис.2).

Рис.1

Рис.2

  Доказательство необходимости . Докажем, что если  точки    C 1 ,  A 1  и  B 1  лежат на одной прямой , то выполнено равенство (1). Для этого проведём через точку  C  прямую, параллельную прямой AB , и обозначим буквой  D  её точку пересечения с прямой  C 1 B 1

• Поскольку  треугольник  AC 1 B 1  подобен треугольнику  CDB 1 , то выполнено равенство(2):

Равенство (1):

• Поскольку  треугольник  C 1 BA 1  подобен треугольнику  A 1 DC , то выполнено равенство(3):

Перемножая равенства (2) и (3), получим:

Что и требовалось доказать.

Доказательство достаточности .

Докажем, что если  выполнено равенство (1) , то точки  C 1 ,  A 1  и    B 1  лежат на одной прямой. Воспользуемся

методом «от противного» . С этой целью проведём прямую

через точки  C 1  и  A 1  и обозначим символом  B 2  точку

пересечения этой прямой с прямой  AC (рис.3)

• Поскольку точки  C 1 ,  A 1  и  B 2  лежат на одной прямой, то выполнено равенство(4):

Рис.3

Кроме того, выполнено равенство(1):

• Разделив равенство (4) на равенство (1), получим равенство:

Следствием которого является равенство(5):

Воспользовавшись  свойствами производных пропорций , из равенства (5) получаем, что точки  B 1   и  B 2  совпадают. Доказательство достаточности завершено.

Теорема Менелая 1 доказана.

ТЕОРИЯ 2

Джованни Чева (1647-1734 гг.)

Итальянский математик и инженер, доказавший теорему Чевы о геометрии треугольника.

Основной заслугой является построение учения о секущих, которое положило начало новой синтетической геометрии.

Джованни Чева был инженером-гидравликом и в качестве такового несколько раз служил правительству Мантуи. Смерть его последовала во время осады Мантуи.

Также он опубликовал одну из первых работ по математической экономике (De re nummeraria, 1711), в которой рассматривались условия стабильности денежной системы Мантуи.

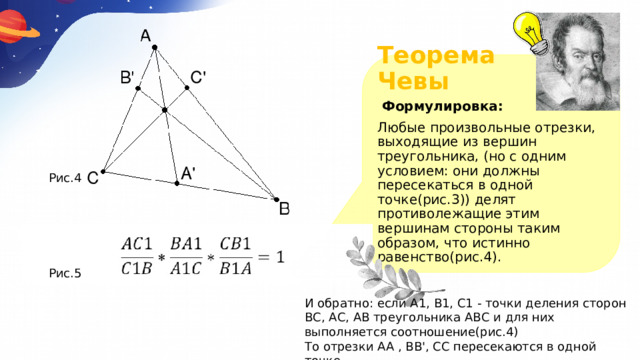
Теорема Чевы

  Формулировка:

Любые произвольные отрезки, выходящие из вершин треугольника, (но с одним условием: они должны пересекаться в одной точке(рис.3)) делят противолежащие этим вершинам стороны таким образом, что истинно равенство(рис.4).

Рис.4

Рис.5

И обратно: если A1, B1, С1 - точки деления сторон ВС, АС, АВ треугольника АВС и для них выполняется соотношение(рис.4)

То отрезки АА , BB', СС пересекаются в одной точке.

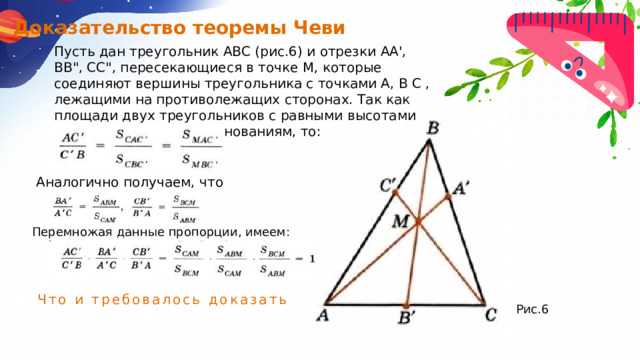
Доказательство теоремы Чеви

Пусть дан треугольник АВС (рис.6) и отрезки АА', ВB", СС", пересекающиеся в точке М, которые соединяют вершины треугольника с точками А, В С , лежащими на противолежащих сторонах. Так как площади двух треугольников с равными высотами пропорциональны их основаниям, то:

Аналогично получаем, что

Перемножая данные пропорции, имеем:

Что и требовалось доказать

Рис.6

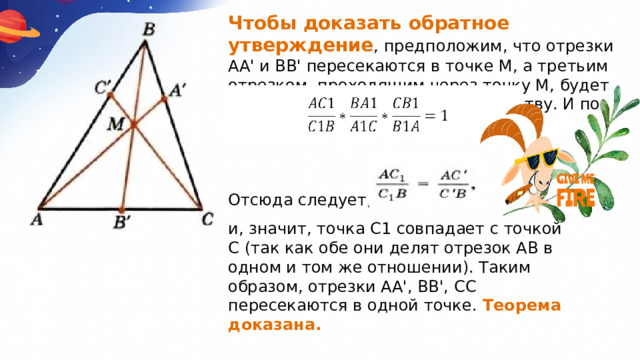
Чтобы доказать обратное утверждение , предположим, что отрезки АА' и ВВ' пересекаются в точке М, а третьим отрезком, проходящим через точку М, будет СС1. Тогда по доказанному равенству. И по условию теоремы:

Отсюда следует, что

и, значит, точка С1 совпадает с точкой С (так как обе они делят отрезок АВ в одном и том же отношении). Таким образом, отрезки АА', ВВ', СС пересекаются в одной точке. Теорема доказана.

Задача 1.

В треугольнике АВС на стороне ВС взята

точка N так, что NC = 3BN; на

продолжении стороны АС за точку А

взята точка М так, что МА=АС. Прямая MN пересекает сторону АВ в точке F.

Найдите: отношение

BF

FA

Решение

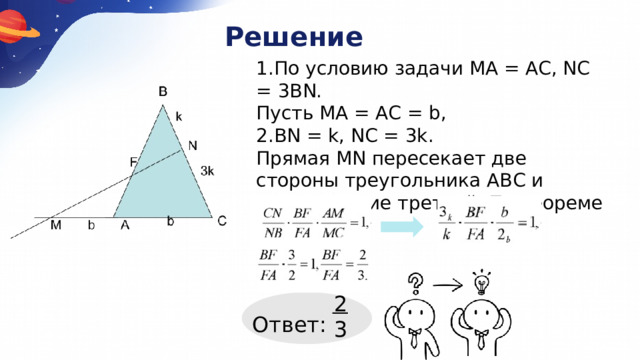
1.По условию задачи МА = АС, NC = 3BN.

Пусть МА = АС = b,

2.BN = k, NC = 3k.

Прямая MN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая:

2

3

Ответ:

Задача 2.

С помощью теоремы Чевы

доказать, что:

Медианы треугольника АВС пересекаются в одной точке

Доказательство

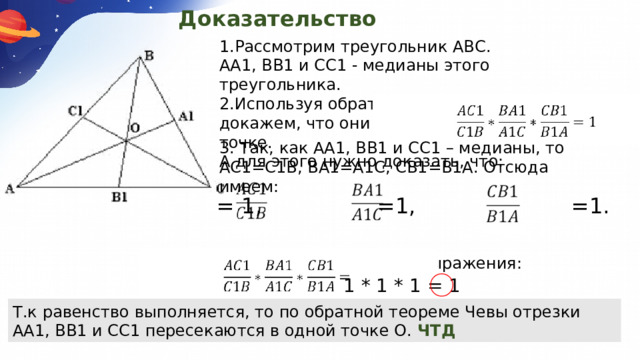
1.Рассмотрим треугольник АВС.

АА1, BВ1 и СС1 - медианы этого треугольника. 2.Используя обратную теорему Чевы, докажем, что они пересекутся в одной точке. А для этого нужно доказать, что:

3. Так, как АА1, BВ1 и СС1 – медианы, то АС1=С1B, BA1=А1С, СВ1=В1А. Отсюда имеем:

4.Перемножим данные выражения:

= 1, =1, =1.

1 * 1 * 1 = 1

Т.к равенство выполняется, то по обратной теореме Чевы отрезки АА1, BВ1 и СС1 пересекаются в одной точке О. ЧТД

Задача 3.

На медиане АА1  треугольника АВС взята точка М,  причём АМ:МА1 = 1:3 

Найти: в каком отношении прямая ВМ  делит сторону  АС.

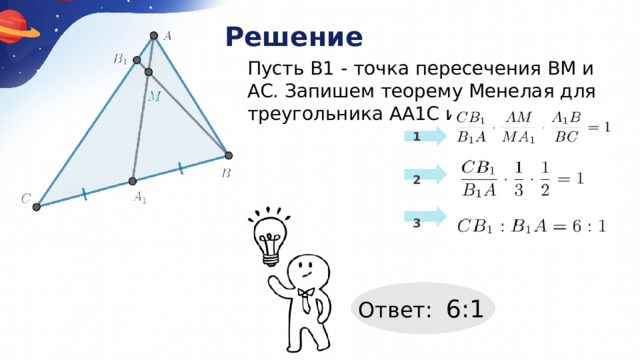
Решение

Пусть В1 - точка пересечения ВМ и АС. Запишем теорему Менелая для треугольника АА1С и прямой BB1 :

1

2

3

Ответ: 6:1

Заключение

Замечательные теоремы Менелая и Чевы, сложные на первый взгляд, оказались просты и интересны. Они находят применение в задачах, в которых присутствуют секущие прямые. Теоремы Чевы и Менелая изучаются в основном курсе геометрии 10 класса. И решение задач с помощью теорем Чевы и Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными. Я думаю, что теоремы Чевы и Менелая должны быть включены в основной курс геометрии 7-9 классов, так как решение задач с помощью этих теорем развивает мышление учеников. В результате проведенной работы, я узнала много интересного и познавательного, научилась применять теоремы в решении задач. Я думаю, что данное исследование, проведённая мной, поможет мне в дальнейшем при подготовке учеников к ОГЭ, ЕГЭ и олимпиадам.

Спасибо за внимание!