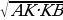-
Угол называется развёрнутым, если обе его стороны лежат на одной прямой.( Развёрнутый угол равен 180°).
-
Две геометрические фигуры называются равными, если их можно совместить наложением.
-
Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
-
Угол называется прямым, если он равен 90°.
-
Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
-
Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).
-
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.
-
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
-
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
-
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
-
Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
-
Треугольник называется равносторонним, если все его стороны равны.
-
В равнобедренном треугольнике углы при основании равны.
-
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
-
(Первый признак равенства треугольников) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
-
(Второй признак равенства треугольников) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
-
(Третий признак равенства треугольников) Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
-
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности.
-
Радиус окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.
-
Отрезок, соединяющий две точки окружности, называется ее хордой.
-
Хорда, проходящая через центр окружности, называется диаметром.
-
Круг — это часть плоскости, ограниченная окружностью.
-
Две прямые на плоскости называются параллельными, если они не пересекаются.
-
При пересечении двух прямых секущей образуется восемь углов: накрест лежащие, односторонние и соответственные.
-
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
-
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
-
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
-
Сумма углов треугольника равна 180°.
-
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
-
Если все три угла треугольника острые, то треугольник называется остроугольным.
-
Если один из углов треугольника тупой, то треугольник называется тупоугольным.
-
Если один из углов треугольника прямой, то треугольник называется прямоугольным.
-
Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две стороны, образующие прямой угол — катетами.
-
В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
-
В прямоугольном треугольнике гипотенуза больше катета.
-
(Неравенство треугольника) Каждая сторона треугольника меньше суммы двух других сторон.
-
Сумма двух острых углов прямоугольного треугольника равна 90°.
-
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
-
В прямоугольном треугольнике медиана, проведенная из прямого угла равна половине гипотенузы.
-
Признаки равенства прямоугольных треугольников: по двум катетам; по катету и острому углу; по гипотенузе и острому углу; по гипотенузе и катету.
-
Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.
-
Сумма длин всех сторон многоугольника называется периметром многоугольника.
-
Сумма углов выпуклого n-угольника равна (n–2)·180°.
-
Четырёхугольник – это многоугольник у которого четыре вершины и четыре стороны.
-
Сумма углов выпуклого четырехугольника равна 360°.
-
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
-
В параллелограмме противоположные стороны равны и противоположные углы равны. Диагонали параллелограмма точкой пересечения делятся пополам.
-
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
-
Трапеция называется равнобедренной, если её боковые стороны равны.
-
Трапеция называется прямоугольной, если один из её углов прямой.
-
(Т. Фалеса) Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
-
Прямоугольником называется параллелограмм, у которого все углы прямые.
-
Диагонали прямоугольника равны.
-
Ромбом называется параллелограмм, у которого все стороны равны.
-
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
-
Квадратом называется прямоугольник, у которого все стороны равны.
-
Все углы квадрата прямые. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
-
Площадь квадрата равна квадрату его стороны ( S=a2).
-
Площадь прямоугольника равна произведению его смежных сторон (S=ab).
-
Площадь параллелограмма равна произведению его основания на высоту (S=ah).
-
Площадь треугольника равна половине произведения его основания на высоту (S= 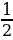 ah).
ah).
-
Площадь прямоугольного треугольника равна половине произведения его катетов (S= 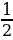 ab).
ab).
-
Площадь трапеции равна произведению полусуммы её оснований на высоту ( S= 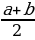 ·h ).
·h ).
-
Площадь ромба равна половине произведения его диагоналей (S= 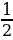 d1·d2).
d1·d2).
-
(Теорема Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. (с2=a2+b2)
-
Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
-
(Формула Герона) Площадь треугольника со сторонами a, b, c выражается формулой S=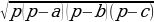 , где p =
, где p = 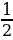 (a+b+c) - полупериметр треугольника.
(a+b+c) - полупериметр треугольника.
-
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
-
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.( AB/A1B1= k ).
-
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.( S1/ S2 = k2).
-
(Первый признак подобия треугольников) Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
-
(Второй признак подобия треугольников) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
-
(Т. Третий признак подобия треугольников) Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
-
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.
-
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны (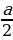 ).
).
-
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
-
Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
-
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.h=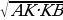
-
Средняя линия трапеции — это отрезок, соединяющий середины ее боковых сторон.
-
Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме(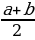 ).
).
-
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
-
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
-
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
-
sin2A+cos2A=1 – основное тригонометрическое тождество.
-
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
-
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
-
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
-
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности.
-
Угол с вершиной в центре окружности называется её центральным углом.
-
Центральный угол измеряется дугой, на которую он опирается.
-
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
-
Вписанный угол измеряется половиной дуги, на которую он опирается.
-
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
-
Вписанный угол, опирающийся на диаметр – прямой.
-
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
-
Четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот называются замечательными точками треугольника.
-
В любой треугольник можно вписать окружность.Около любого треугольника можно описать окружность.
-
Не во всякий четырёхугольник можно вписать окружность.Около четырёхугольника не всегда можно описать окружность.
-
В любом описанном четырёхугольнике суммы противоположных сторон равны.
-
В любом вписанном четырёхугольнике сумма противоположных углов равна 180°.






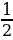 ah).
ah).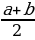 ·h ).
·h ).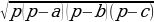 , где p =
, где p = 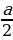 ).
).