Теория вероятности в жизни

Теория вероятностей.

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным. Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие. 

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории: дискретная и непрерывная.

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Теория вероятностей в жизни

1. Игры в кости

Кости — одна из древнейших игр. Инструментом для игры являются кубики (кости) в количестве от одного до пяти в зависимости от вида игры. Суть игры состоит в выбрасывании кубиков и дальнейшем подсчёте очков, количество которых и определяет победителя. Разновидности игры предполагают разный подсчёт очков.

1. Коды на ….

– сейфах

– телефонные номера

– пароль в социальных сетях (агент, одноклассники и т.д.)

1. Лотереи

Лотерея – организованная игра, при которой распределение выгод и убытков зависит от случайного извлечения того или иного билета или номера (жребия, лота). Кто из нас не мечтал выиграть в лотерею миллион! Но все мы реалисты, и понимаем, что вероятность такого выигрыша очень мала. Ведь игра в лотерею – это игра с судьбой, попытка поймать удачу; и чем больше выигрыш стоит на кону – тем сильнее ощущения!

1. Карточные игры

Карточная игра — игра с применением игральных карт, характеризуется случайным начальным состоянием, для определения которого используется набор (колода).

Важным принципом практически всех карточных игр является случайность порядка карт в колоде. Перед использовании той же колоды в следующей игре карты в ней перемешиваются (перетасовываются).

1. Игровые автоматы

Известно, что в игровых автоматах скорость вращения барабанов зависит от работы микропроцессора, повлиять на который нельзя. Но можно вычислить вероятность выигрыша на игровом автомате, в зависимости от количества символов на нем, числа барабанов и других условий. Однако выиграть это знание вряд ли поможет.

Основные формулы «Теории вероятности»

Определение вероятности события:

где n — общее число равновероятных исходов; m — число исходов, благоприятных событию A.

Вероятность произведения независимых событий

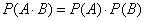
где A и B независимые события (т.е. вероятность одного события остается неизменной не зависимо от того, произошло или нет другое событие).

Вероятность суммы несовместных событий

где A и B несовместные события (т.е. в ходе проведения эксперимента не могут произойти одновременно).

Если событие А может произойти только при выполнении одного из событий B1, B2, ..., Bn, которые образуют полную группу несовместных событий — вероятность события А вычисляется по формуле полной вероятности:

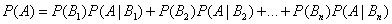
Существуют ещё множество формул теории вероятности.

3