Тест №4
Конус
1 Вариант
Выберите верное утверждение.
а) Конус может быть получен в результате вращения равностороннего треугольника вокруг его стороны;
б) прямая, проходящая через вершину конуса и центр его основания, называется осью конуса;
в) разверткой боковой поверхности конуса является круговой сегмент;
г) площадь боковой поверхности усеченного конуса равна произведению суммы длин окружностей оснований на образующую;
д) сечение конуса, проходящее через ось, есть круг.
2. Образующая конуса, равная 8 см, наклонена к плоскости основания под углом 30°. Найдите площадь осевого сечения конуса.
а) 2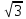 см2; б)4
см2; б)4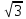 см2; в) 16
см2; в) 16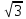 см2; г) 8
см2; г) 8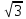 см2; д) 32
см2; д) 32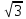 см2.
см2.
3. Радиус основания конуса равен 10 см, а высота равна 15 см. Найдите площадь сечения конуса плоскостью, параллельной основанию и находящейся на расстоянии 2 см от вершины конуса.
а) 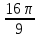 см2; б)
см2; б) 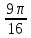 см2; в)
см2; в) 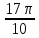 см2; г) 5625
см2; г) 5625 см2; д) 9
см2; д) 9 см2.
см2.
4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 2 см. Эта хорда стягивает дугу в 90°. Угол между образующими в сечении равен 60°. Найдите площадь боковой поверхности конуса.
а) 2 см2; б) 2
см2; б) 2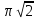 см2; в) 4
см2; в) 4 см2; г) 4
см2; г) 4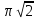 см2; д) 8
см2; д) 8 см2.
см2.
5. Угол при вершине осевого сечения конуса равен 60°, сумма длин его высоты и образующей равна 2 см. Найдите площадь полной поверхности конуса.
а) 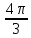 см2; б) 12
см2; б) 12 (7 - 4
(7 - 4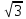 ) см2; в)
) см2; в) 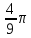 (3+2
(3+2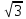 ) см2; г)
) см2; г)  см2;
см2;
д) 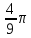 см2.
см2.
6. Радиусы оснований усеченного конуса равны 12 и 6 см, а образующая наклонена к плоскости основания под углом 45°. Найдите высоту усеченного конуса.
а) 4 см; б) 3 см; в) 12 см; г) определить нельзя; д) 6 см.
7. Полукруг свернут в конус. Найдите угол при вершине осевого сечения конуса.
а) 30°; б) 45°; в) 60°; г) 90°; д) 120°.
8. Длина образующей усеченного конуса равна 29 см, высота – 20 см, радиусы оснований относятся, как 5:9. Найдите периметр осевого сечения усеченного конуса.
а) 205 см; б) 102,5 см; в) 47,25 см; г) 26,25 см; д) 73,5 см.
9. В усеченный конус, радиусы оснований которого равны 2 и 4, вписан шар. Найдите площадь боковой поверхности усеченного конуса.
а) Определить нельзя; б) 9 ; в) 72
; в) 72 ; г) 18
; г) 18 ; д) 36
; д) 36 .
.
10. Радиус верхнего основания, высота, образующая и радиус нижнего основания усеченного конуса составляют арифметическую прогрессию с разностью 4. Вычислите площадь полной поверхности усеченного конуса.
а) 144 ; б) 1256
; б) 1256 ; в) 1584
; в) 1584 ; г) 1440
; г) 1440 ; д) 360
; д) 360 .
.
2 Вариант
Выберите неверное утверждение.
а) Конус может быть получен в результате вращения прямоугольного треугольника вокруг одного из его катетов;
б) прямая, проходящая через вершину конуса и центр его основания, называется осью конуса;
в) площадь боковой поверхности конуса может быть вычислена по формуле
Sбок. =  r(r + l);
r(r + l);
г) осевым сечением усеченного конуса является равнобедренная трапеция;
д) конус называется равносторонним, если его осевое сечение – правильный треугольник.
2. Образующая конуса, равная 4 см, наклонена к плоскости основания под углом 60°. Найдите площадь осевого сечения конуса.
а) 8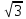 см2; б)
см2; б)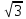 см2; в) 16
см2; в) 16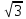 см2; г) 4
см2; г) 4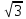 см2; д) 2
см2; д) 2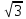 см2.
см2.
3. Радиус основания конуса и его высота равны 7 см. Найдите площадь сечения конуса плоскостью, проходящей параллельно основанию на расстоянии 4 см от его вершины.
а) 16 см2; б) 12
см2; б) 12 см2; в) 8
см2; в) 8 см2; г)49
см2; г)49 см2; д) 3,0625
см2; д) 3,0625 см2.
см2.
4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 2 см. Эта хорда стягивает дугу в 60°. Угол между образующими в сечении равен 90°. Найдите площадь боковой поверхности конуса.
а) 2 см2; б) 2
см2; б) 2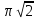 см2; в) 4
см2; в) 4 см2; г) 4
см2; г) 4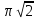 см2; д) 8
см2; д) 8 см2.
см2.
5. Угол при вершине осевого сечения конуса равен 60°, сумма длин его радиуса и образующей равна 2 см. Найдите площадь полной поверхности конуса.
а)  см2; б) 4
см2; б) 4 (2
(2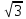 +3) см2; в)
+3) см2; в)  (2
(2 ) см2; г)
) см2; г)  см2;
см2;
д)  см2.
см2.
6. Радиусы оснований усеченного конуса равны 10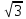 и 6
и 6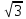 см, а образующая наклонена к плоскости основания под углом 60°. Найдите высоту усеченного конуса.
см, а образующая наклонена к плоскости основания под углом 60°. Найдите высоту усеченного конуса.
а) 4 см; б) 6 см; в) 12 см; г) определить нельзя; д) 3 см.
7. Найдите угол между высотой и образующей конуса, если площадь боковой поверхности конуса равна 2, а площадь полной его поверхности равна 3.
а) 120°; б) 90°; в) 60°; г) 45°; д) 30°.
8. Длина образующей усеченного конуса равна 13 см, высота – 12 см. Найдите радиусы оснований, если периметр осевого сечения усеченного конуса равен 56 см.
а) 6 см и 12 см; б) 5 см и 10 см; в) 5 см и 15 см; г) 10 см и 12 см; д) 12 см и 13 см.
9. В усеченный конус, образующая которого равна 6, вписан шар. Найдите площадь боковой поверхности усеченного конуса.
а) Определить нельзя; б) 9 ; в) 72
; в) 72 ; г) 18
; г) 18 ; д) 36
; д) 36 .
.
10. Найдите площадь полной поверхности усеченного конуса, если его радиусы равны 21 и 11, а длина диагонали осевого сечения равна 40.
а) 1394 ; б) 832
; б) 832 ; в) 1273
; в) 1273 ; г) 953
; г) 953 ; д) 562
; д) 562 .
.







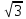 см2; б)4
см2; б)4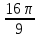 см2; б)
см2; б) 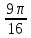 см2; в)
см2; в) 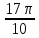 см2; г) 5625
см2; г) 5625 см2; д) 9
см2; д) 9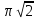 см2; в) 4
см2; в) 4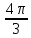 см2; б) 12
см2; б) 12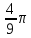 (3+2
(3+2







География 10 класс ФГОС
Технология 3 класс ФГОС
Воспитательные мероприятия для...
Увлекательная информатика
Электронная тетрадь по математике 5...
Биология 6 класс
Электронная тетрадь по истории Древнего...
Электронная тетрадь по русскому языку...
© 2019, Затеева Валентина Павловна 4031 25
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы