Вариант 1
Т – 1
Заполните пропуски (многоточия), чтобы получилось верное утверждение или правильная формулировка определения, правила.
-
Запись из чисел, соединённых знаками арифметических действий, называют … выражением.
-
Если в числовом выражении выполнить указанные действия, то получим число, которое называют … этого числового выражения.
-
Два числовых выражения, соединённые знаком «=», образуют числовое… .
-
Если значения левой и правой частей числового равенства совпадают, то равенство называют … .
-
Выражения 2a-3, (2a+4):(3-a), (a-b)(a+b),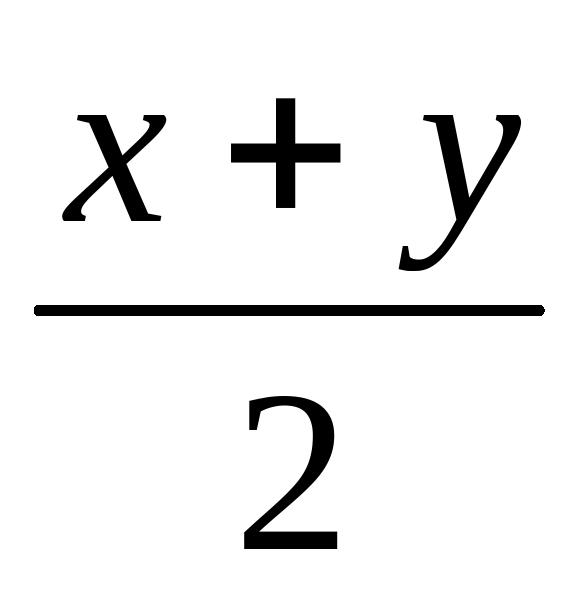 являются … выражениями.
являются … выражениями.
-
Если вместо букв, входящих в алгебраическое выражение, подставить числа и выполнить действия, то полученное в результате число называют … алгебраического выражения.
-
Формула a=2n, где n – натуральное число, формула … числа.
-
Формула a=2n+1,где n – натуральное число или ноль, - формула … числа.
-
Формула a+b=b+a выражает … закон сложения.
-
Формула a(b+c)=ab+ac выражает … закон.
-
В формулах a+b=b+a, ab=ba,
(ab)c=a(bc),(a+b)+c=a+(b+c), a(b+c)=ab+ac
числа a, b, c - … числа.
-
Переместительный закон умножения записывается в виде формулы … .
-
Сочетательный закон сложения записывается в виде формулы … .
-
a - (b + c) = a + (…b …c)
-
Сумма трёх последовательных нечётных чисел, меньшее из которых 2n+5, равна … .
Вариант 2
Т – 1
Заполните пропуски (многоточия), чтобы получилось верное утверждение или правильная формулировка определения, правила.
-
Выражения, например, 3 4; 15 : 3 – 2; 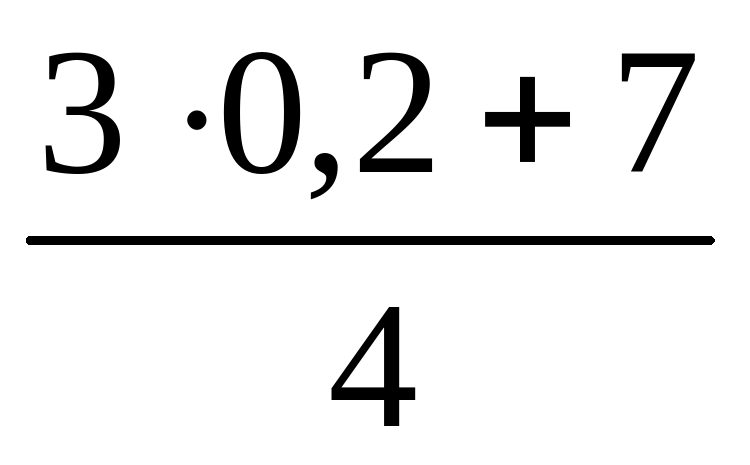 называют … выражениями.
называют … выражениями.
-
Равенство называют верным, если значения левой и правой частей числового равенства … .
-
Если в выражение 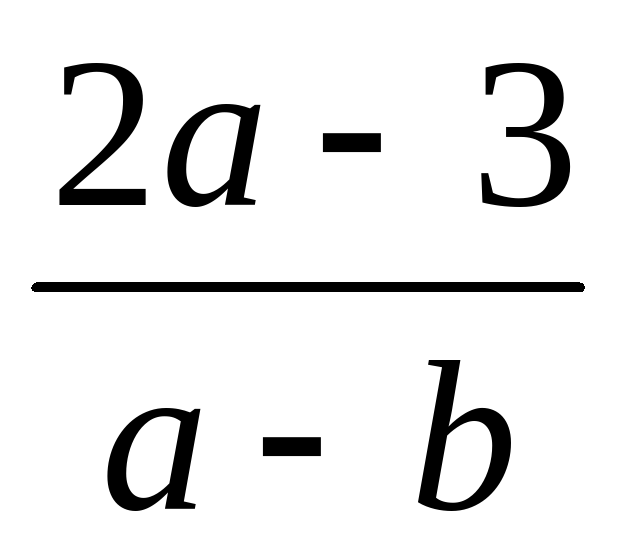 вместо a подставить 10, а вместо b подставить 5, то полученное в результате выполнения действий число называют … алгебраического выражения.
вместо a подставить 10, а вместо b подставить 5, то полученное в результате выполнения действий число называют … алгебраического выражения.
-
Выражения 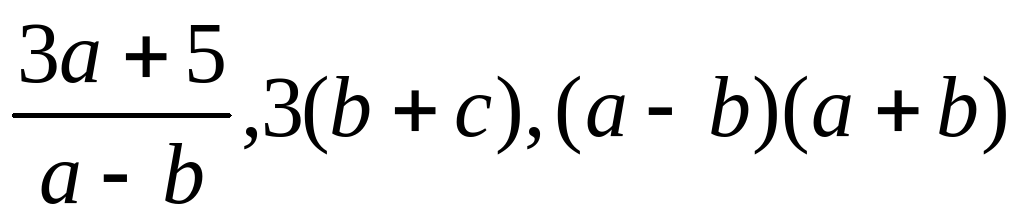 - примеры … выражений.
- примеры … выражений.
-
Запись, состоящую из нескольких алгебраических выражений, соединённых знаками «+» или «-», называют алгебраической … .
-
Если к алгебраическому выражению прибавить алгебраическую сумму, заключённую в скобки, то скобки можно опустить, а знак каждого слагаемого этой алгебраической суммы … .
-
Переместительный закон сложения записывается в виде формулы … .
-
Формула ab=ba выражает … закон умножения.
-
Формула ( a+b)+c=a+(b+c) выражает … закон сложения.
-
Формула чётного натурального числа а имеет вид: а=…, где … - натуральное число.
-
Формула b=2k-1 , где k – натуральное число, - формула … натурального числа b.
-
Сочетательный закон умножения записывается в виде формулы… .
-
Распределительный закон умножения записывается в виде формулы … .
-
a – (-b – c) = a + (…b …c).
-
Сумма трёх последовательных чётных чисел, меньшее из которых 4n, равна … .
Т-2
Установите, истинны или ложны следующие утверждения:
-
13 + 6 3 = (13 + 6) 3.
-
В алгебраических выражениях: 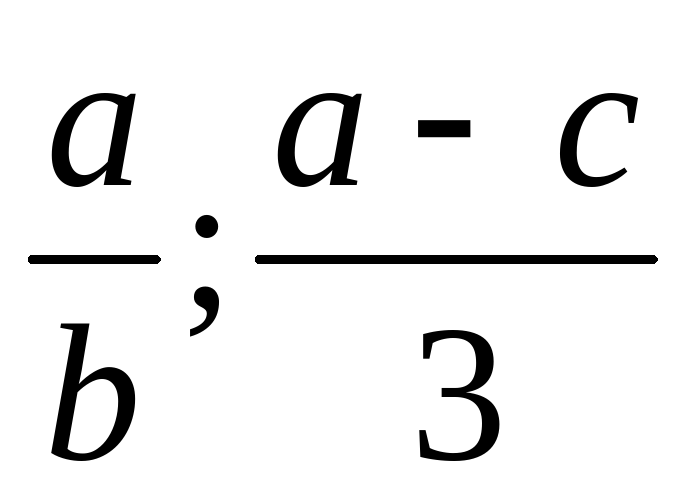 a, b, c могут принимать любые числовые значения.
a, b, c могут принимать любые числовые значения.
-
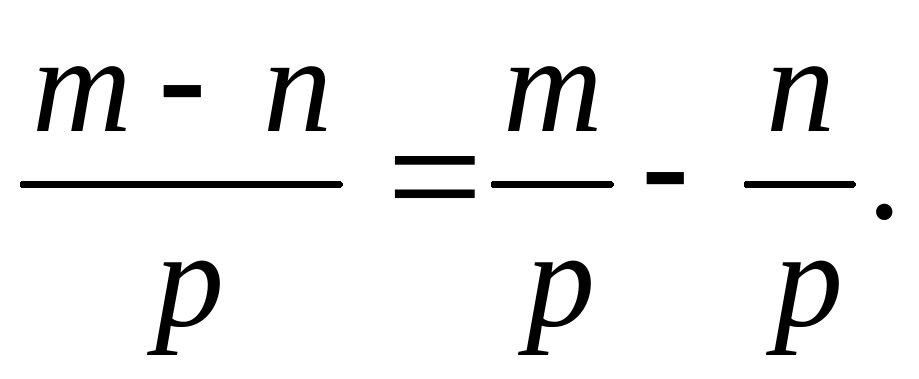
-
a – b = a + (-b).
-
2x + ( y – z) = 2x + y – z.
-
a – (2b + 2c) = a – 2b –2c.
-
–(k – l) = l – k.
-
(2a + 3b) – (a – b) = -a + 4b.
-
x + (-y –2x) – 2y = -x + y.
-
Число a = 2n, где n – натуральное число, - чётное число.
-
Произведение трёх любых чётных чисел кратно 8.
-
При любых значениях а значение выражения 3(2а+1)-(5-(1-6а)) отрицательно.
Т – 3
В каждом задании установите верный ответ из числа предложенных.
-
Запишите в виде числового выражения:
а) удвоенную сумму чисел 17 и 33.
А. 2(17 + 33); Б. 2 + (17 + 33); В. 100.
б) произведение суммы и разности чисел 88 и 12.
А. (88-12)(88 + 12); Б. 88 12(88+12)(88-12); В. 7600.
-
Запишите: а) половину разности чисел a и b;
А. 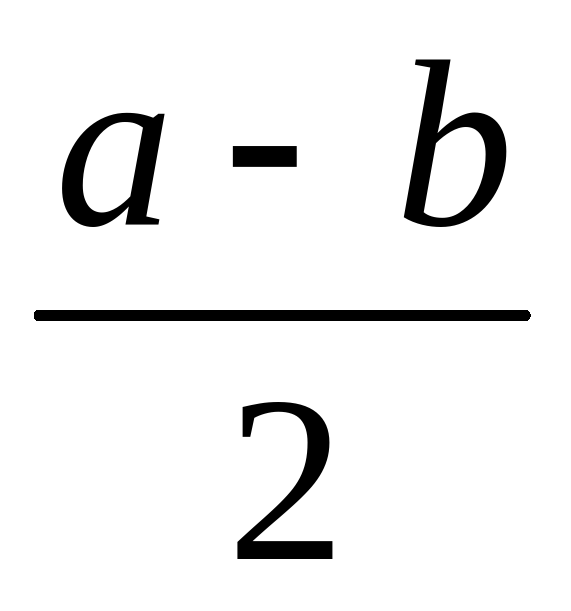 ; Б.
; Б. 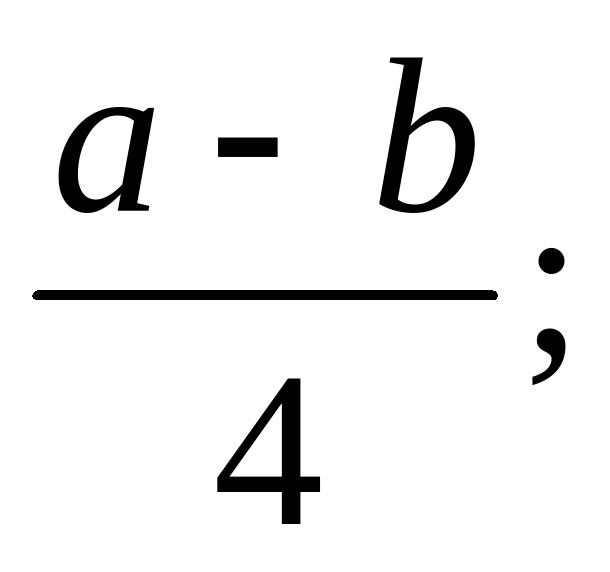 В. 2(a – b).
В. 2(a – b).
б) удвоенное произведение чисел c и d;
А. bc + 2; Б. 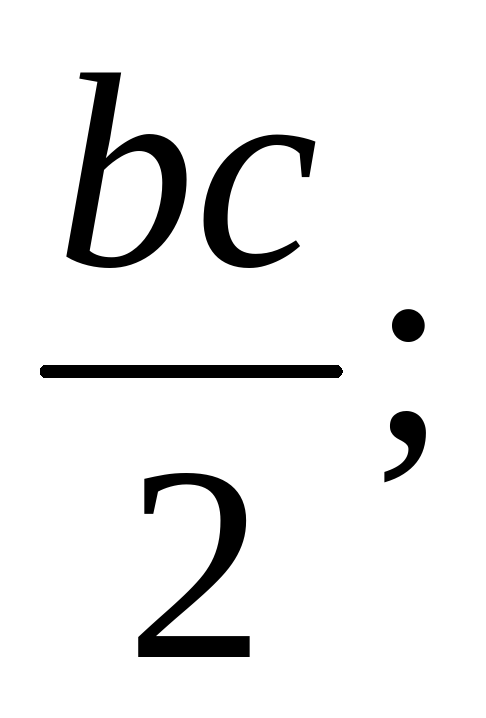 В. 2bc.
В. 2bc.
в) произведение суммы чисел a и b и числа c.
А. c(a + b); Б. b(a + c); В. a(b + c).
-
Из формулы F = ma выразите m через F и а.
А. M = Fa; Б. 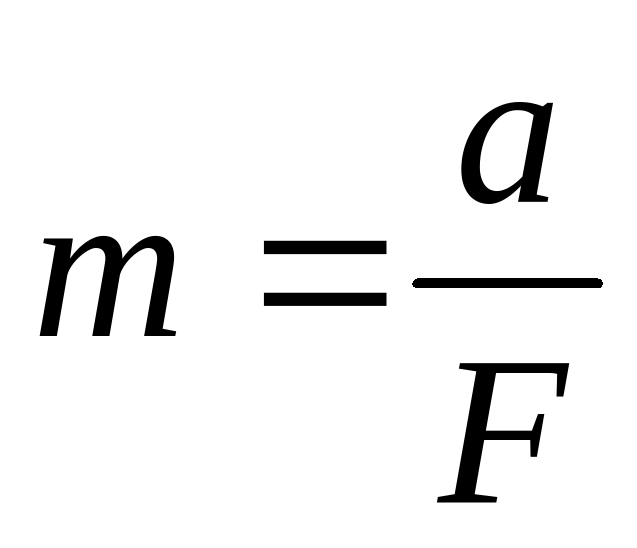 ; B. m =
; B. m =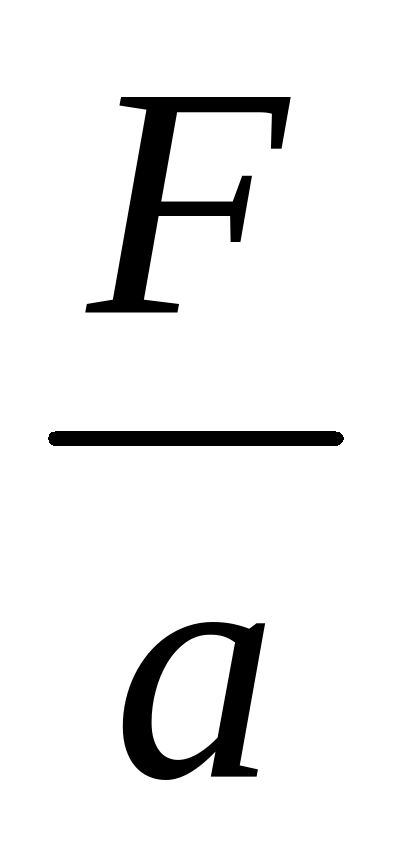 .
.
-
Упростите выражение: а) 3(2 - х) + 2(4х + 1);
А. 11х + 8; Б. 5х + 8; В. –5х – 8;
б) 3у – (у – 2(у + 1)).
А. 4у – 2; Б. 4у + 2; В. –2.
-
Запишите формулу: а) чётного натурального числа b;
А. b=2n, где n - натуральное число;
Б. b=2n, n – целое число; В. b=2n+1, n – целое число;
б) нечётного натурального числа а.
А. a=2n, n –целое число; Б. a=2n+1, n –натуральное число или ноль; В. a=2n-1, n –натуральное число.
-
Напишите формулу решения задачи: в кинотеатре имеется а рядов по с мест в каждом и ещё по 2 откидных места в каждом ряду. Сколько всего мест в кинотеатре?
А. а + с + 2а; Б. ас + 2а; В. 2с + ас.
-
Запишите произведение трёх последовательных натуральных чисел, большее из которых равно а.
А. а(а+1)(а+2); Б. (а-2)(а-1)а; В. (а-1)а(а+1).
-
Укажите, какие числовые значения могут принимать а и с в алгебраическом выражении 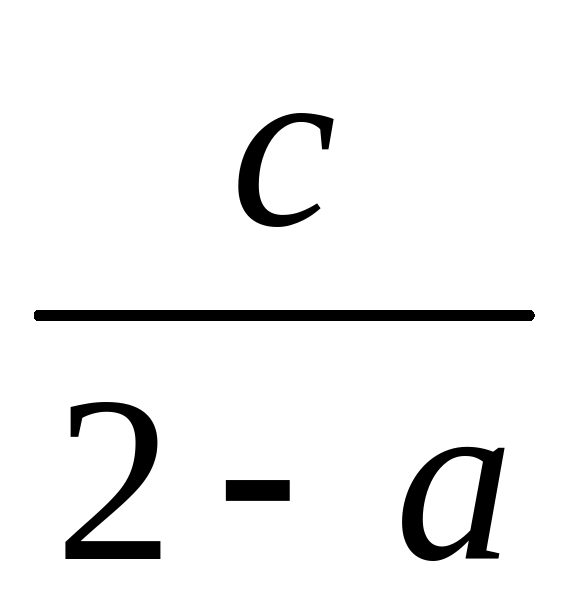 .
.
А. а и с – любые числа; Б. а2, с – любое число; В. а0,с 2.
Т – 2
Установите, истинны или ложны следующие утверждения:
-
7 13 + 6 = 7 (13 + 6).
-
В алгебраических выражениях: 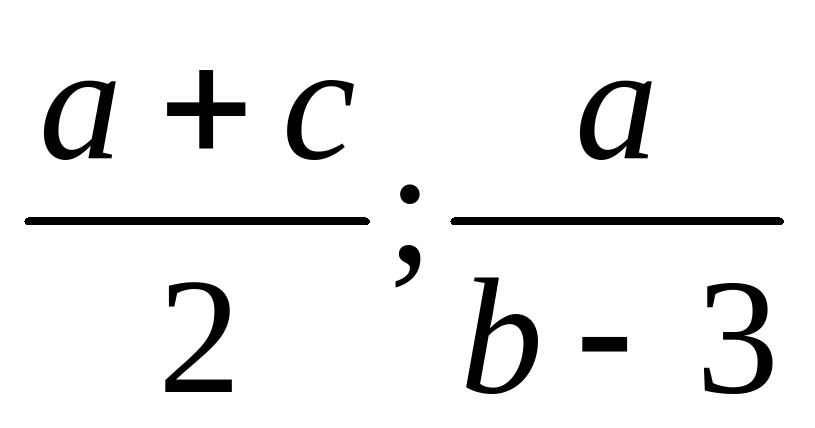 a, b, c могут принимать любые числовые значения.
a, b, c могут принимать любые числовые значения.
-
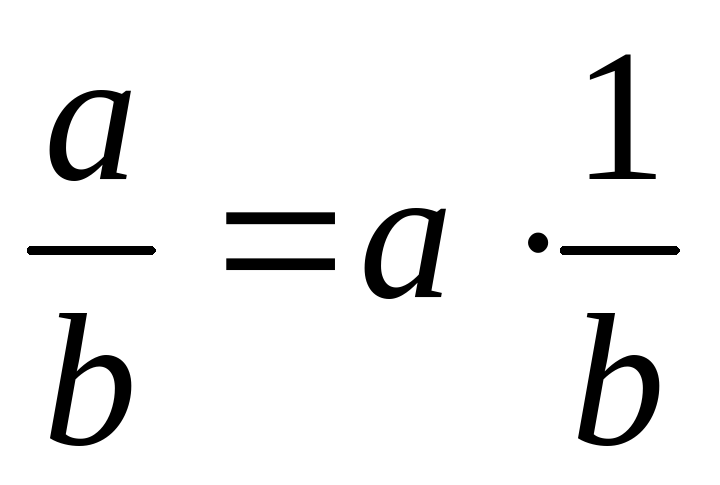 .
.
-
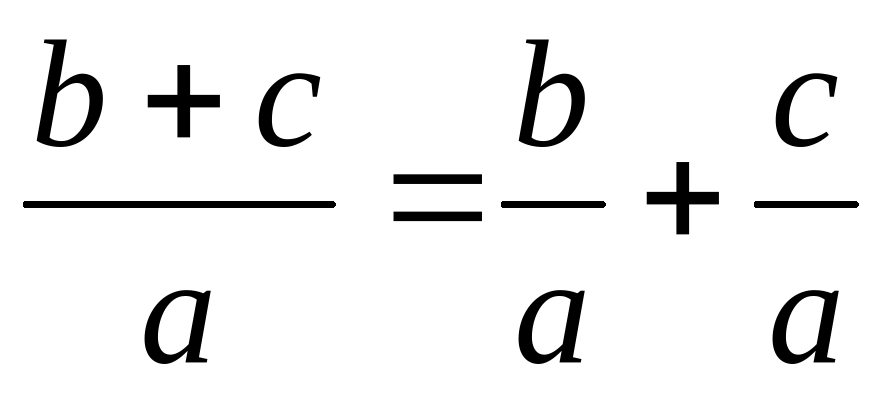 .
.
-
x – (-y) + (-z) = x + y – z.
-
3a – (b + c) = 3a – b – c.
-
–(-1,5m + n) = -n + 1,5m.
-
(5a – b) – (-a + b) = 6a + 2b.
-
x – (2x – y) – 3y = -x – 4y.
-
Число b=2n-1, где n – натуральное число или ноль, - нечётное число.
-
Разность чисел 8m – n и 3m + 4n, где n и m - заданные числа, делится на 5.
-
При любых значениях а значение выражения 1,5(1 - 2а)- – (4 – (3а + 5)) положительно.
Т – 3
В каждом задании установите верный ответ из числа предложенных.
-
Запишите в виде числового выражения:
а) произведение суммы и разности чисел 55 и 45;
А. (45 + 55)(45 – 55); Б. (55 + 45)(55 – 45); В. 1000.
б) удвоенное произведение чисел 2,5 и 10.
А. 2 2,5 10; Б. 2,5 10 + 2; В. 50.
-
Запишите: а) половину суммы чисел а и с;
А. 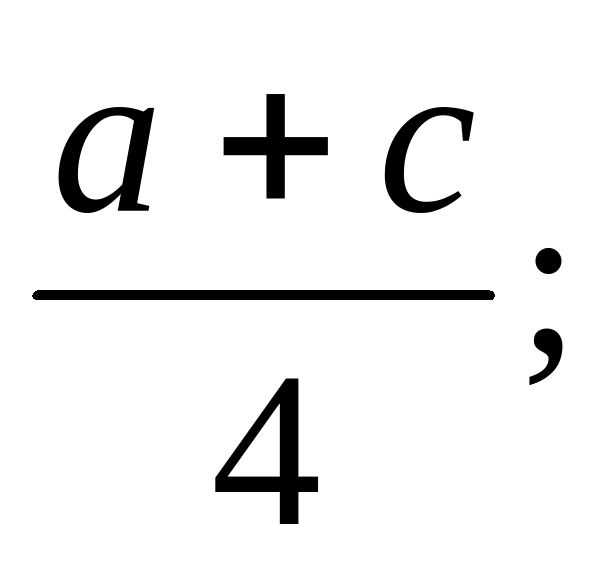 Б.
Б. 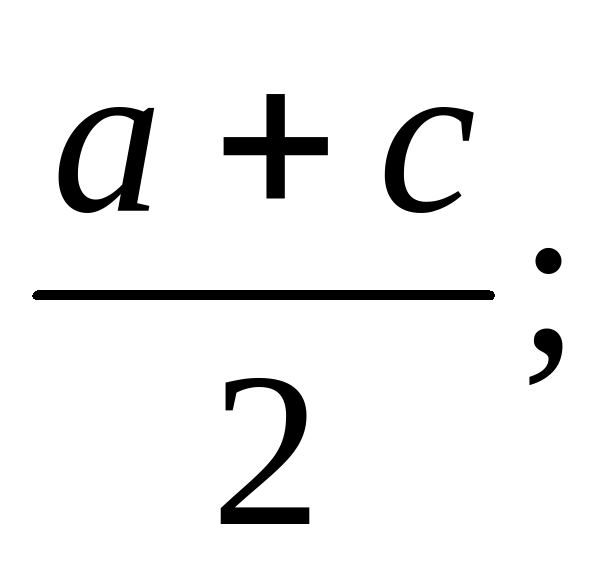 В. 0,2(а + с).
В. 0,2(а + с).
в) произведение разности чисел b и c и числа a.
А. (b – c)a; Б. (c – b)a; B. ac – ab.
-
Из формулы S = vt выразите v через S и t.
А. 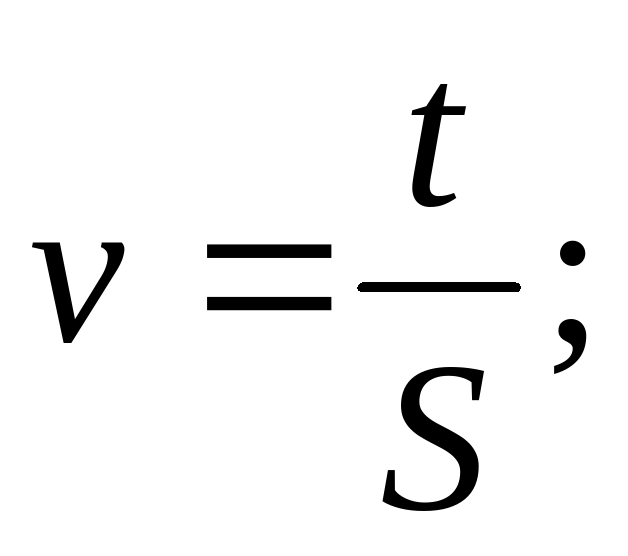 Б.
Б. 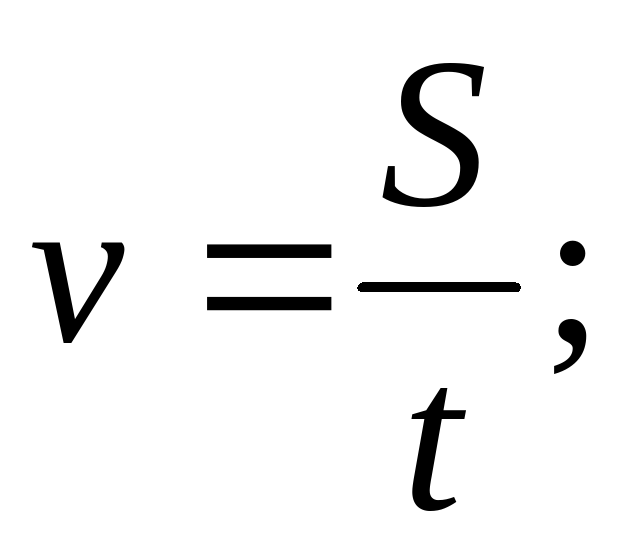 B.
B. 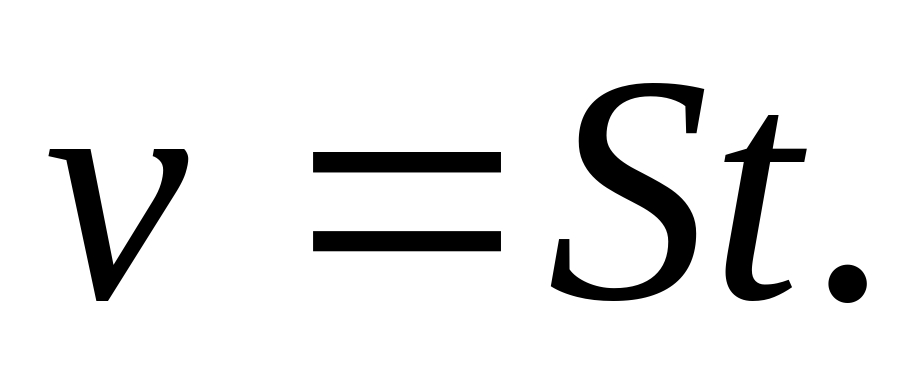
-
Упростите выражение: а) (х + у) – 10(2х – у);
А. 11 у – 19х; Б. –9у – 19х; В. 11у + 21х.
б) 4а + (3а – (а + 3)).
А. 6а – 3; Б. 6а + 3; В. 8а + 3.
-
На сковороде поместили а рядов пирожков, в каждом ряду - по к пирожков. Сколько всего пирожков на сковороде?
а) составьте формулу решения задачи;
А. с = а + к; Б. с = ак; В. с = а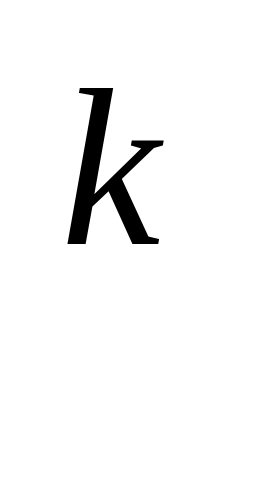 .
.
б) проведите вычисления при а = 5; с = 4.
А. 625; Б. 20; В. 9.
-
Напишите формулу решения задачи: определить стоимость р всей покупки, если куплено 2 батона хлеба по х руб. и 3 булочки по у руб.
А. р = 2х 3у; Б. р = 2х + 3у; В. р = х² + у².
-
Запишите произведение трёх последовательных натуральных чисел, меньшее из которых равно к.
А. (к – 1)к(к + 1); Б. к(к + 1)(к + 2); В. к(к – 1)(к – 2).
-
Укажите, какие числовые значения могут принимать a и b в алгебраическом выражении 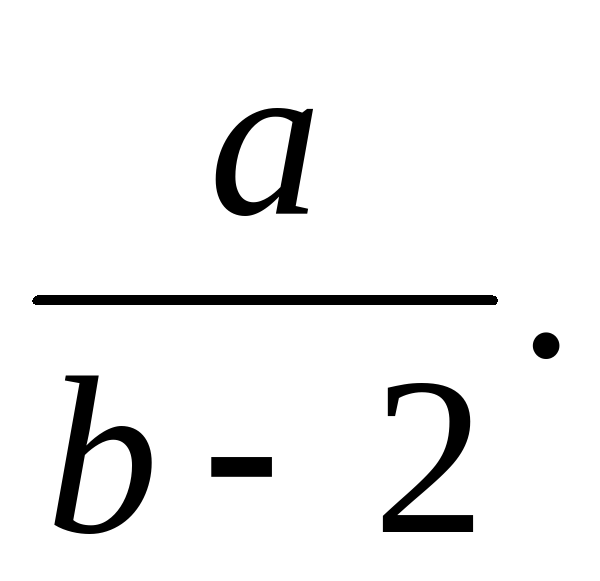
А. а и b - любые числа; Б. а – любое число, b 2;
В. а 0, b 2.