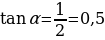Тест по математической грамотности для учеников 8-9 классов.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
1.
| Объекты | Баня | Морковь | Картофель | Капуста |
| Цифры | 5 | 4 | 2 | 6 |

Ирина купила участок, чтобы заняться фермерством. План ее огорода изображен на рисунке, сторона каждой клетки равна 2 м. Участок планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить баню. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под постройку дома. На поле рядом с ним планируется посадить капусту. Поле, обозначенное на плане цифрой 3, планируется засеять репой. Поле, ближайшее к гаражу, планируется отвести под картофель. Оставшееся поле будет засеяно морковью. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м2 гравием, требуется 0,2 м3 материала.
Контекст – личный.
Содержание математического образования – пространство и форма.
Мыслительная деятельность – формулировать (формулировать ситуацию на языке математики)
Объект оценки – определение номеров объектов.
Уровень сложности - 1
Формат ответа – вопрос с выбором ответа
Критерии оценивания – 0 или 1 балл
2. Гравий продаётся в больших мешках по 2 м3. Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между участками 2,3,4,6,7?
Решение.
Площадь одной клетки равна 2 · 2 = 4 м2. Значит, площадь пространства, которую необходимо засыпать гравием, равна
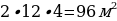 .
.
Чтобы засыпать 4 м2 гравием, требуется 0,2 м3 материала. Следовательно, понадобится 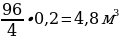 гравия. В одном мешке 2 м3 гравия. Значит, придётся купить 3 мешка с гравием.
гравия. В одном мешке 2 м3 гравия. Значит, придётся купить 3 мешка с гравием.
Контекст – личный.
Содержание математического образования – пространство и форма.
Мыслительная деятельность – применять (применять математические понятия, факты, процедуры)
Объект оценки – определение количества мешков.
Уровень сложности - 1
Формат ответа – вопрос с кратким ответом
Критерии оценивания – 0 или 1 балл
3. Найдите площадь территории, которая не занята постройками. Ответ дайте в квадратных метрах.
Решение.
Площадь всего участка равна
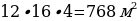 .
.
Площадь гаража равна 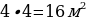
Площадь жилого дома равна 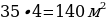 .
.
Площадь бани равна 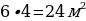

Значит, площадь территории, которая не занята постройками, равна
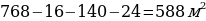 .
.
Контекст – личный.
Содержание математического образования – пространство и форма.
Мыслительная деятельность – применять (применять площадь, свойства площадей)
Объект оценки – определение площади.
Уровень сложности - 2
Формат ответа – вопрос с развернутым ответом
Критерии оценивания – 0 или 1, или 2 балла
4. Найдите расстояние между противоположными углами (диагональ) участка в метрах.
Решение.
Найдём расстояние между противоположными углами участка по теореме Пифагора:
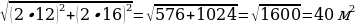 .
.
Контекст – личный.
Содержание математического образования – пространство и форма.
Мыслительная деятельность – применять (применять теорему ПИФАГОРА)
Объект оценки – определение расстояния.
Уровень сложности - 2
Формат ответа – вопрос с развернутым ответом
Критерии оценивания – 0 или 1, или 2 балла
5. В семье Ирины, состоящей из 4 человек, проживающих в г.Чусовой, решили заменить крышу бани, при этом выяснилось, что существует несколько способов перекрытия крыш. Есть определенная закономерность архитектурного построения здания, при котором расчет угла наклона крыши определяется отношением высоты крыши к ширине дома как 1:4. Этот способ определения угла крыши очень приблизительный, так как не учитывает ни выбор кровельного материала, ни ветровые и снеговые нагрузки в данном регионе.

Определите, какой должна быть высота крыши, если ее ширина 4м, длина 4м.
Ответ: 1м.
Контекст – профессиональный.
Содержание математического образования – пространство и форма.
Мыслительная деятельность – применять. Выполнить простое и прямое математическое задание.
Объект оценки – определение высоты крыши.
Уровень сложности - 1
Формат ответа – вопрос с выбором ответа
Критерии оценивания – 0 или 1 балл
6. Рассчитайте, чему равен тангенс угла наклона крыши.
А) 0,25 Б) 0,5 В) 1 Г) 0,45
Ответ: 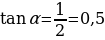
Контекст – профессиональный.
Содержание математического образования – изменения и зависимости.
Мыслительная деятельность – применять. Применить стандартный алгоритм.
Объект оценки – нахождение тангенса угла наклона крыши.
Уровень сложности - 2
Формат ответа – вопрос с выбором ответа
Критерии оценивания – 0 или 1 балл
7. Компания «Дом для семьи» занимается строительством коттеджных посёлков. Для остекления коттеджей она закупает у фирмы по изготовлению окон различные виды окон. Образцы окон с размерами в миллиметрах представлены на рисунках.
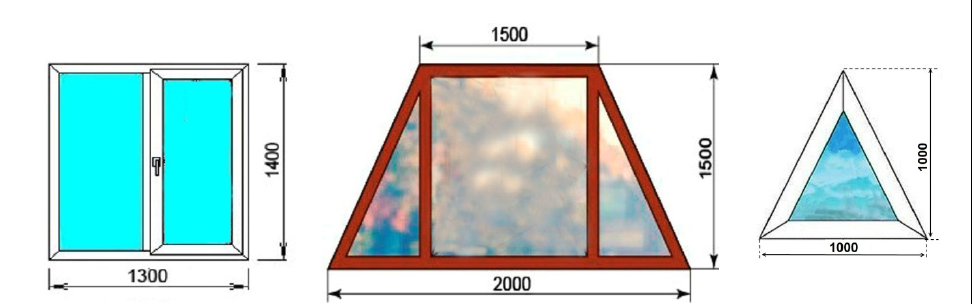
Цены одного квадратного метра различных видов окон представлены в таблице ниже.
| Вид окна | Цена за 1 м2 |
| Треугольное | 3 460 руб. |
| Прямоугольное | 5 700 руб. |
| Трапециевидное | 6 000 руб. |
Отметьте «Верно» или «Неверно» для каждого утверждения в таблице, приведённой ниже.
| Утверждение | Верно | Неверно |
| Один квадратный метр треугольного окна дешевле одного квадратного метра прямоугольного окна на 2240 рублей. | + |
|
| Площадь одного окна в форме трапеции в 3 раза больше площади одного треугольного окна. |
| + |
Контекст – профессиональный.
Содержание математического образования – пространство и форма.
Мыслительная деятельность – интерпретировать (интерпретировать, использовать и оценивать математические результаты)
Объект оценки – заполнение готовой таблицы.
Уровень сложности - 1
Формат ответа – задание с несколькими краткими ответами.
Критерии оценивания – 0 или 1 балл
Фирма по изготовлению окон предоставляет покупателям следующие скидки:
- При заказе товара на сумму свыше 100 000 рублей предоставляется скидка 5%.
- При заказе товара на сумму свыше 300 000 рублей предоставляется скидка 10%.
Какую сумму за покупку 20 прямоугольных окон заплатит строительная компания фирме с учётом скидок?
Ответ:______________________ руб.
Решение: __________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________
Контекст – профессиональный.
Содержание математического образования – пространство и форма.
Мыслительная деятельность – применять. Применить стандартный алгоритм.
Объект оценки – вычисление суммы за покупку окон.
Уровень сложности - 2
Формат ответа – задание с развернутым ответом.
Критерии оценивания – 0 или 1 балл, или 2 балла.







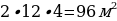 .
.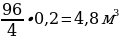 гравия. В одном мешке 2 м3 гравия. Значит, придётся купить 3 мешка с гравием.
гравия. В одном мешке 2 м3 гравия. Значит, придётся купить 3 мешка с гравием.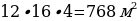 .
.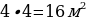
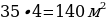 .
.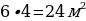

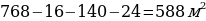 .
.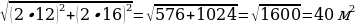 .
.