Тест по теме: «Аксиомы стереометрии и способы задания плоскости»
1 - вариант
1. К основным фигурам в пространстве относятся: а) точка, прямая, угол; б) точка, прямая, плоскость; в) точка, плоскость, угол; г) прямая, угол, плоскость.
2.Какое из следующих утверждений верно: а) любые четыре точки лежат в одной плоскости; б) любые три точки не лежат в одной плоскости; в) любые четыре точки не лежат в одной плоскости; г) через любые три точки не лежащие на одной прямой проходит плоскость и при том только одна.
3. Могут ли прямая и плоскость иметь две общие точки? а) могут; б) не могут; в) оба ответа верны.
4. Сколько общих точек могут иметь две различные плоскости? а) три; б) две; в) несколько; г) бесчисленное множество.
5. Точки А, В, С лежат на одной прямой. Точка D не лежит на ней. Через каждые три точки проведена плоскость. Сколько различных плоскостей при этом получилось? а) 2; б) 3; в) 1; г) 4; д) бесчисленное множество.
6. Прямые α, b и с попарно пересекаются. Могут ли прямые α, b и с лежать в одной плоскости? а) да; б) нет; в) оба ответа верны.
7. Выберите верное утверждение а) если одна точка прямой лежит в плоскости, то и все точки прямой лежат в этой плоскости; б) через прямую и не лежащую на ней точку проходит плоскость и при том только одна; в) через две пересекающие прямые провести плоскость нельзя; г) любые две плоскости не имеют общих точек
8. Две плоскости пересекаются по прямой с. Точка М лежит только в одной из плоскостей. Что можно сказать о взаимном положении точки М и прямой с. а) через точку М прямая с не проходит; б) никакого вывода сделать нельзя; в) точка М лежит на прямой с д) другой ответ.
9. Прямые α и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые α и b. Что можно сказать о взаимном положении прямых α, b и с. а)все прямые лежат в разных плоскостях; б) прямые α и b лежат в одной плоскости, а прямая с в ней не лежит; в) все прямые лежат в одной плоскости; г) прямая с совпадает с одной из прямых: или с α, или с b.
10.Точки А,В, С не лежат на одной прямой. М 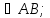 К
К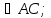 Х
Х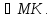 Выберите верные утверждения. а) Х
Выберите верные утверждения. а) Х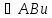 точки Х и М совпадают; б) Х
точки Х и М совпадают; б) Х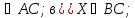 г) точка Х
г) точка Х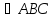 ;
;
Тест по теме: «Аксиомы стереометрии и способы задания плоскости»
2 - вариант
1. Как называется раздел геометрии изучающий фигуры в пространстве? а) планиметрия; б) тригонометрия; в) стереометрия; г) геометрия.
2.Сколько плоскостей можно провести через прямую? а) 1; б) 2; в) 3; г) бесчисленное множество.
3. Выберите верное утверждение: а) любые три точки лежат в одной плоскости; б) любые четыре точки лежат в одной плоскости; в) любые четыре точки не лежат в одной плоскости; г) через любые три точки проходит плоскость, и притом только одна.
4. Сколько общих точек может быть у прямой и плоскости? а) две; б) три; в) несколько; г) множество.
5. Могут ли две плоскости иметь: а) только одну общую точку; б) только две общие точки; в) только одну общую прямую?
6. Точки А,В,С, D не лежат в одной плоскости. Выбрать верное утверждение. а) Точки А,В,С, D лежат на одной прямой; б) любые три из них не могут лежать на одной прямой); в) прямые АВ и СD пересекаются; г) плоскости АВС и АВD пересекаются.
7. Если три точки не лежат на одной прямой, то положение плоскости в пространстве они : а) не определяют в любом случае; б) определяют, но при дополнительном условии; в) определяют в любом случае; г) другой ответ.
8. Точки А,В,С лежат на одной прямой. Точка D не лежит на ней. Сколько плоскостей можно провести через эти точки? а) 1; б) 2; в) 3; г) плоскость провести нельзя.
9. Выбрать верное утверждение: а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости; б) если прямая проходит через одну из вершин треугольника, то и вся прямая лежит в плоскости данного треугольника; в) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости; г) все утверждения неверны.
10. Три прямые проходят через одну точку и не лежат в одной плоскости. Через каждые две из них проведена плоскость. Сколько плоскостей можно провести через эти прямые? а) 1; б) 2; в) 3; г) много.





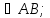 К
К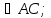 Х
Х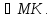 Выберите верные утверждения. а) Х
Выберите верные утверждения. а) Х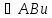 точки Х и М совпадают; б) Х
точки Х и М совпадают; б) Х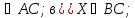 г) точка Х
г) точка Х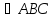 ;
; 









