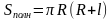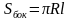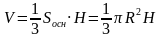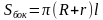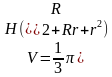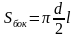Тест по теме "Конус"

ТО 107 Математика

Преподаватель: Водяхина Н. В. Электронный адрес почты: nata.vodiahina2014@yandex.ru

Задание выдано 12.05.20. Задание выполнить до 14.05.20!

Прочитать внимательно лекцию и выполнить тест! А-Л (1 вариант), М-Я (2 вариант)

КОНУС

Определение. Конусом (круговым конусом), называется тело, которое состоит из круга- основания конуса, точки, не лежащей в плоскости этого круга- вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания- образующие конуса.

О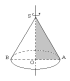 пределение Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.

Конус может быть получен вращением прямоугольного треугольника вокруг одного из катетов.

т. S – вершина конуса

круг (О,ОА) – основание конуса

SA=SB – образующие конуса

Отрезок SO – высота конуса

Прямая SO – ось конуса

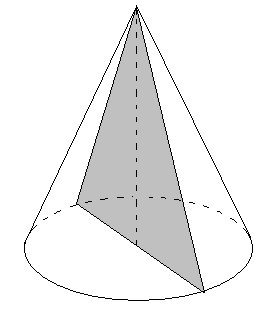
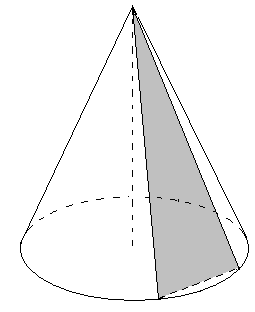
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса.

Т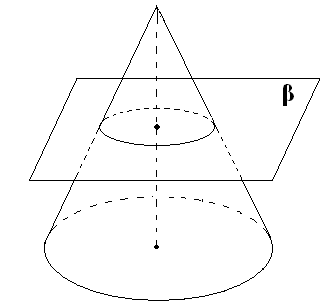 еорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность - по окружности с центром на оси конуса

Возьмем произвольный конус и проведем секущую плоскость, перпендикулярную его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усеченным конусом.

Определение. Усеченным конусом называется часть конуса, заключенная между его основанием и сечением, параллельным основанию. Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса, а отрезок, соединяющий их центры- высотой усеченного конуса.

h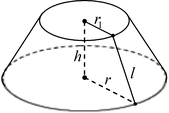 — высота усеченного конуса,

r₁ и r₂ — радиусы основания усеченного конуса, l — образующая усеченного конуса.

Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.

Осевым сечением усеченного конуса является равнобокая трапеция.

Площадь полной поверхности конуса: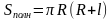

Площадь боковой поверхности: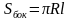

Объём конуса: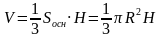

Площадь полной поверхности усечённого конуса:

Площадь боковой поверхности: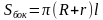

Объём усечённого конуса: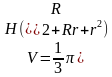

Тест по теме: «Конус»

Вариант №1

1. Конус может быть получен вращением…

1) равностороннего треугольника вокруг его стороны;

2) прямоугольного треугольника вокруг одного из его катетов;

3) прямоугольного треугольника вокруг гипотенузы.

2. Площадь боковой поверхности конуса можно вычислить по формуле…

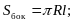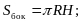1) 2) 3)

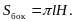
3. Сечением конуса плоскостью, перпендикулярной оси цилиндра, является…

1) треугольник; 2) прямоугольник; 3) круг.

4. Расстояние от центра основания конуса до плоскости сечения, проходящей через вершину конуса, равно длине отрезка…

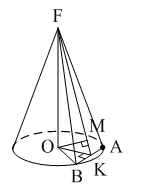
1) OB; 2) OK; 3) OM.

5. Развёрткой боковой поверхности конуса является круговой…

1) сегмент; 2) сектор; 3) слой.

6. Площадь полной поверхности конуса равна…

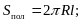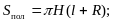1) 2) 3)

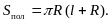
7. Наибольший периметр имеет сечение конуса, проходящее через его вершину и хорду, стягивающую дугу в…

1) 60°; 2) 90°; 3) 180°.

8. Через вершину конуса и хорду ВС проведена плоскость.

Тогда угол между этой плоскостью и плоскостью основания это угол…

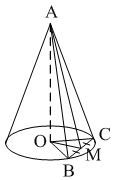
1) ABO; 2) AMO; 3) BAC.

Вариант №2

1. Конус может быть получен вращением…

1) прямоугольного треугольника вокруг гипотенузы;

2) равнобедренного треугольника вокруг медианы, проведённой к основанию;

3) тупоугольного треугольника вокруг одной из его сторон.

2. Площадь боковой поверхности конуса нельзя вычислить по формуле…

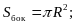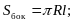1) 2) 3)

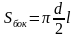
3. Сечением конуса плоскостью, проходящей через вершину конуса и хорду основания, не может быть…

1) прямоугольный треугольник;

2) равнобедренный треугольник;

3) разносторонний треугольник.

4. Расстояние от центра основания конуса до плоскости сечения, проходящей через вершину конуса, равно длине отрезка…

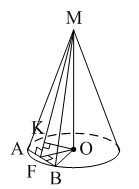
1) OF; 2) OK; 3) OB.

5. а – образующая конуса, b – высота конуса. Тогда верно, что…

1) a b; 2) a = b; 3) a b.

6. Площадь полной поверхности конуса, у которого осевым сечением является равносторонний треугольник со стороной а, равна…

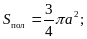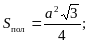1) 2) 3)

7. Наибольшую площадь имеет сечение конуса, проходящее через его вершину и хорду, стягивающую дугу в…

1) 60°; 2) 90°; 3) 180°.

8. Через вершину конуса и хорду AB проведена плоскость.

Тогда угол между этой плоскостью и плоскостью основания – это угол…

1) ACB; 2) OAC; 3) CKO.