 Геометрия 7 класс. 1 вариант
Геометрия 7 класс. 1 вариант
-
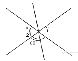
Углы, отмеченные на рисунке одной дугой
равны. Найдите угол α. Ответ дайте в градусах
-
Периметр равнобедренного треугольника равен 19,
а основание — 9. Найдите боковую сторону треугольника.

-
В равнобедренном треугольнике ABC с
основанием AC внешний угол при вершине C
равен 123°. Найдите величину угла ABC.
-
Укажите номера верных утверждений.
-
Если угол острый, то смежный с ним угол также является
острым.
-
Периметр квадрата можно найти, умножив длину его стороны на 4.
-
В плоскости все точки, равноудалённые от заданной точки,
лежат на одной окружности.
Если утверждений несколько, запишите их через точку с
запятой в порядке возрастания.
-
На какой угол (в градусах) поворачивается минутная стрелка пока часовая проходит 6 градусов?
-
Д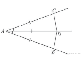 ва острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол.
ва острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол.
-
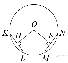
На сторонах угла 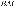 и на его биссектрисе
и на его биссектрисе
отложены равные отрезки  и
и 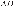 .
.
Величина угла  равна 160°.
равна 160°.
Определите величину угла 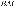 .
.
-
В окружности с центром  проведены две
проведены две
равные хорды 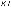 и
и 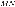 . На эти хорды опущены
. На эти хорды опущены
перпендикуляры 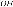 и
и 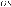 .
.
Докажите, что 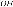 и
и 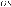 равны.
равны.
-
В треугольнике АВС углы А и С равны 20° и 60°
соответственно. Найдите угол между высотой ВН и биссектрисой BD.
-
Два острых угла прямоугольного треугольника относятся
как 4:5. Найдите больший острый угол.
11. Какие из следующих утверждений верны?
1) Если угол равен 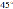 , то вертикальный с ним угол равен
, то вертикальный с ним угол равен 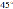 .
.
2) Любые две прямые имеют ровно одну общую точку.
3) Через любые три точки проходит ровно одна прямая.
12. Сколько спиц в колесе, если угол между соседними
спицами равен 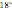 ?
?
13. Какой угол (в градусах) образуют минутная и часовая стрелки часов
в 5 ч?
14. Площадь прямоугольного земельного участка равна 9 га, ширина участка равна 150 м. Найдите длину этого участка в метрах.
1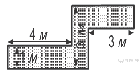 5. Определите, сколько необходимо закупить пленки
5. Определите, сколько необходимо закупить пленки 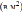 для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
1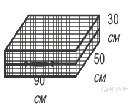 6. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в
6. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в 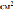 ) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно
) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно
(без загибов).
Г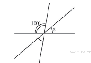 еометрия 7 класс. Вариант 2
еометрия 7 класс. Вариант 2
-
Углы, отмеченные на рисунке одной
дугой, равны. Найдите угол  .
.
-
Периметр равнобедренного треугольника
р авен 196, а основание — 96. Найдите боковую
авен 196, а основание — 96. Найдите боковую
сторону треугольника.
-
В равнобедренном треугольнике ABC с
основанием AC внешний угол при вершине C
равен 120°. Найдите величину угла ABC.
-
Укажите номера верных утверждений.
-
Если две стороны одного треугольника равны двум сторонам
другого треугольника, то треугольники равны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его
биссектрисой.
Если утверждений несколько, запишите их через точку с запятой
в порядке возрастания.
-
На какой угол (в градусах) поворачивается минутная стрелка пока
ч асовая проходит 4 градуса?
-
Два острых угла прямоугольного треугольника
относятся как 1:89. Найдите больший острый угол.
-
Найдите величину угла  ,
,
если  — биссектриса угла
— биссектриса угла  ,
,
 — биссектриса угла
— биссектриса угла  .
.
-
На стороне АС треугольника АВС выбраны точки
D и E так, что отрезки AD и CE равны
Оказалось, что отрезки BD и BE тоже равны.
Докажите, что ∆ АВС — равнобедренный.
-
Прямая AD, перпендикулярная медиане ВМ
∆АВС, делит её пополам. Найдите сторону АС,
если сторона АВ равна 4. (8)
-
Два острых угла прямоугольного треугольника относятся
как 2:7. Найдите больший острый угол. Ответ дайте в градусах.
11. Какие из следующих утверждений верны?
1) Если угол равен , то вертикальный с ним угол равен .
2) Любые две прямые имеют ровно одну общую точку.
3) Через точку на плоскости проходит ровно
одна прямая.
12.Сколько спиц в колесе, если угол между соседними
спицами равен ?
13. Какой угол (в градусах) образуют минутная и часовая стрелки часов
в ч?
14. Площадь прямоугольного земельного участка равна га, ширина участка равна м. Найдите длину этого участка в метрах.
1 5. Определите, сколько необходимо закупить пленки 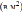 для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
1 6. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в 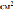 ) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов)
) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов)
В ариант 3
ариант 3
-
Найдите величину угла DOK, если OK — биссектриса
угла AOD, ∠DOB = 108°. Ответ дайте в градусах.
-
П ериметр равнобедренного треугольника равен 186,
ериметр равнобедренного треугольника равен 186,
а основание — 86. Найдите боковую сторону
треугольника.
-
В равнобедренном треугольнике ABC с основанием
AC внешний угол при вершине C равен 102°.
Найдите величину угла ABC.
-
Какие из следующих утверждений верны?
-
Если при пересечении двух прямых третьей прямой внутренние
накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
2) Если угол равен 60°, то смежный с ним равен 120°.
3) Если при пересечении двух прямых третьей прямой внутренние
односторонние углы равны 70° и 110°, то эти две прямые
параллельны.
-
Через любые три точки проходит не более одной прямой.
-
На какой угол (в градусах) поворачивается минутная стрелка пока
часовая проходит  ?
?
-
Д ва острых угла прямоугольного треугольника относятся как 2:43. Найдите больший острый угол.
-
На сторонах угла 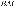 , равного 20°, и на его
, равного 20°, и на его
биссектрисе отложены равные отрезки
 и
и 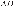 . Определите величину
. Определите величину
угла  .
.

-
На стороне АС треугольника АВС выбраны точки
D и E так, что углы АDB и BEC равны
Оказалось, что отрезки AЕ и CD тоже равны.
Докажите, что ∆АВС — равнобедренный.
-
В треугольнике АВС углы А и С равны
20° и 50° соответственно. Найдите угол
Между высотой ВН и биссектрисой BD.
-
Два острых угла прямоугольного треугольника относятся
как 4:5. Найдите больший острый угол.
11. Какие из следующих утверждений верны?
1) Если угол равен , то вертикальный с ним угол равен .
2) Через любые две точки на прямой можно провести бесконечно
много прямых.
3) Смежные углы равны.
12.Сколько спиц в колесе, если угол между соседними спицами
равен ?
13. Какой угол (в градусах) образуют минутная и часовая стрелки
часов в ч?
14. Площадь прямоугольного земельного участка равна га, ширина
участка равна м. Найдите длину этого участка в метрах.
15. Определите, сколько необходимо закупить пленки 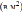 для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
16. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в 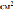 ) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно
) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно
(без загибов).
В ариант 4
ариант 4
-
Найдите величину угла AOK, если OK —
биссектриса угла AOD, ∠DOB = 64°.
-
П ериметр равнобедренного треугольника равен 296, а основание — 96. Найдите боковую сторону треугольника.
ериметр равнобедренного треугольника равен 296, а основание — 96. Найдите боковую сторону треугольника.
-
В равнобедренном треугольнике ABC с основанием
AC внешний угол при вершине C равен 100°.
Найдите величину угла ABC.
-
Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
-
Если при пересечении двух прямых третьей прямой
соответсвенные углы равны по 65°, то эти две прямые параллельны.
-
Если при пересечении двух прямых третьей прямой внутренние
накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
-
Какой угол (в градусах) описывает минутная стрелка за 10 мин?
-
Д ва острых угла прямоугольного треугольника относятся как 37:53. Найдите больший острый угол.
-
На сторонах угла 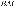 , равного 40°, и на
, равного 40°, и на
его биссектрисе отложены равные отрезки
 и
и 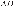 . Определите величину
. Определите величину
угла  .
.
-
Н а стороне АС треугольника АВС выбраны
а стороне АС треугольника АВС выбраны
точки D и E так, что отрезки AD и CE равны
Оказалось, что углы АDB и BEC тоже равны.
Докажите, что ∆АВС — равнобедренный.
-
Прямая AD, перпендикулярная медиане ВМ
треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
-
Два острых угла прямоугольного треугольника относятся
как . Найдите больший острый угол.
11. Какие из следующих утверждений верны?
1) Если угол равен , то смежный с ним угол равен .
2) Любые две прямые имеют ровно одну общую точку.
3) Через любые три точки проходит ровно одна прямая.
12. Сколько спиц в колесе, если угол между соседними
спицами равен ?
-
. Какой угол (в градусах) образуют минутная и часовая стрелки часов в ч?
-
Площадь прямоугольного земельного участка равна га, ширина участка равна м. Найдите длину этого участка в метрах.
-
Определите, сколько необходимо закупить пленки 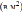 для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
-
Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в 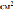 ) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно
) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно
(без загибов).
В ариант 5
ариант 5
-
На прямой AB взята точка M.
Луч MD — биссектриса угла CMB. Известно,
Что ∠DMC = 60°. Найдите угол CMA.
-
Периметр равнобедренного треугольника равен 96,
а основание — 46. Найдите боковую сторону треугольника.
основание — 46. Найдите боковую сторону треугольника.
-
В равнобедренном треугольнике ABC с
основанием AC внешний угол при вершине C
равен 98°. Найдите величину угла ABC.
-
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум
углам другого треугольника, то такие треугольники равны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является
его медианой.
-
Какой угол (в градусах) образуют минутная и часовая стрелки
часов в 5 ч?
-
Два острых угла прямоугольного треугольника относятся как
1 1:79. Найдите больший острый угол.
-
На сторонах угла 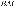 , равного 60°, и на
, равного 60°, и на
его биссектрисе отложены равные отрезки
 и
и 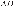 . Определите
. Определите
величину угла  .
.
-
В окружности с центром  проведены две
проведены две
равные хорды 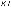 и
и 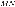 . На эти хорды
. На эти хорды
опущены перпендикуляры 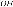 и
и 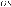 .
.
Докажите, что 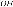 и
и 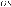 равны.
равны.
-
Прямая AD, перпендикулярная
медиане ВМ треугольника АВС,
делит угол ВАС пополам. Найдите
сторону АС, если сторона АВ равна 3.
-
Два острых угла прямоугольного треугольника относятся
как 4:5. Найдите больший острый угол. Ответ дайте в градусах.
11. Какие из следующих утверждений верны?
1) Если угол равен , то смежный с ним угол равен .
2) Любые две прямые имеют ровно одну общую точку.
3) В равнобедренном треугольнике все углы равны.
12. Сколько спиц в колесе, если угол между соседними спицами равен
?
13. Какой угол (в градусах) образуют минутная и часовая стрелки часов
в ч?
14. Площадь прямоугольного земельного участка равна га, ширина участка равна м. Найдите длину этого участка в метрах.
1 5. Определите, сколько необходимо закупить пленки 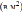 для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
1 6. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в 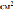 ) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно
) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно
(без загибов).
Зачёт 7 класс по теме «Начальные геометрические сведения»
1 вариант
1. Основные геометрические фигуры – это_____________________________
2. Две прямые могут иметь ______________ точку_____________________
или ___________________________________________________________
3 Луч – это _________________________________________ (Изобразить, обозначить)
4 Угол называется развёрнутым если__________________ (Изобразите его, обозначьте)
(Сравните его град. меру с прямым углом)
5. Середина отрезка – это ____________________________ (Изобразите, обозначьте)
6.
А
7. Прямой угол – это ______________(Изобразите, обозначьте, укажите его град. меру).
8. Прямая разбивает плоскость _______________________________________
9. Если точки лежат в разных полуплоскостях то отрезок ________________
10. Углы измеряются _______________________________________________
11. Два отрезка называются равными если _____________________________
12. Какова бы ни была прямая, существуют точки_______________________
13. Теорема – это утверждение ______________________________________
14. Три точки А, В, С лежат на одной прямой. Известно, что АВ = 17,5см; ВС = 11,4см. Какой может быть длина АС? Сделайте чертёж.
15. Точка С лежит на отрезке РМ. Какая из точек С, Р, М лежит между двумя другими?(сделайте чертёж)__________________________________________
16. Запишите равные элементы треугольников
1 7. Точка С лежит на отрезке АВ.
АС = 4см, АВ = 9см. Какова длина отрезка ВС?
(сделайте чертёж)
18 Прямые называются параллельными если _______
19. Запишите обозначение угла, его
вершину и стороны.
20. Между сторонами угла AOB= 80° проходит луч OC. Найдите углы AOC, COB, если угол СОВ на 40 больше угла АОС.
21. Через точку, не лежащую на данной прямой, можно провести __________
(сделать рисунок)
Зачёт 7 класс по теме «Начальные геометрические сведения»
2 вариант
1. Через две точки можно провести (сколько прямых)_____________________
2 Отрезок – это________________________________________
(изобразить, обозначить)
3 Прямая – это______________________________________________________
4 Угол называется тупым если_______________________ (Изобразите его, обозначьте).
(Сравните его град. меру с прямым углом).
5.
М____________________К
Измерьте отрезок, используя линейку, найдите его середину, сделайте соответствующие записи.
6.
7. Две прямые называются параллельными если __________ (постройте, обозначьте)
8. Из трёх точек на прямой одна и только_______________________________
9. Если точки лежат в одной полуплоскости, то отрезок___________________
10. Два угла называются равными если_________________________________
11. Через точку не лежащую на данной прямой можно провести на плоскости________
12. Аксиома – это утверждение ______________________________________
13. Каков бы ни был треугольник, существует на плоскости ______________
14. Три точки С, Т, Р лежат на одной прямой. Известно, что СТ = 7,3см; ТР = 4,1см. Какой может быть длина отрезка СР? Сделайте чертёж.
15. Отрезок ХУ пересекает прямую а, а отрезок ХМ не пересекает эту прямую. Пересекает ли, прямую а отрезок УМ? (сделайте чертёж) ________
1 6. Луч ОВ проходит между лучами ОК и ОМ. Угол КОМ равен 120 градусов, угол КОВ равен 30 градусов. Чему равен угол МОВ? (сделайте чертёж)_____________________________________
17. Приведите примеры геометрических фигур.
1 8. Запишите вершины и стороны треугольника
19. Запишите обозначение угла,
его вершину и стороны
20. Между сторонами угла AOB= 120° проходит луч OC. Найдите углы AOC, COB, если угол СОВ на 20 больше угла АОС.
21. Через точку, не лежащую на данной прямой, можно провести __________ (сделайте чертёж)
Задачи по теме «Смежные и вертикальные углы».
1 – вариант.
-
Найдите углы смежные с углами: а) 30⁰ б) 60⁰
-
Могут ли два смежных угла быть оба: а) острыми б) прямыми
Объясните ответ.
-
Найдите смежные углы, если а) один из них на 30⁰ больше другого; б) один из них в 8 раз больше другого.
-
Какой угол образуют часовая и минутная стрелки часов, когда они показывают а) 6 часов б) 2 часа
-
Найдите смежные углы, если их градусные меры относятся как
1) 2:3 2) 22:23
6. Один из углов, которые получаются при пересечении двух прямых, равен
40⁰. Чему равны остальные углы.
-
Сумма двух углов, которые получаются при пересечении двух прямых, равна 50⁰. Найдите эти углы.
-
Один из углов, которые получаются при пересечении двух прямых, в 4 раза
больнее другого. Чему равны остальные углы.
-
Один из углов, которые получаются при пересечении двух прямых, на 50⁰ меньше другого. Найдите эти углы.
-
Найдите углы, которые получаются при пересечении двух прямых, если сумма трёх из них равна 270⁰.
-
Чему равен угол между биссектрисой и стороной данного угла, равного а) 80⁰ б) 172⁰
-
Найдите угол, если его биссектриса образует со стороной угол, равный а) 35⁰ б) 89⁰
-
Найдите угол между биссектрисой и продолжением одной из сторон данного угла, равного а) 50⁰ б) 140⁰
-
Из вершины развёрнутого угла АОС в одну полуплоскость проведены лучи ОК и ОР. Чему равен
-
Из вершины развёрнутого угла АОС в одну полуплоскость проведены лучи ОК и ОР. Чему равен
-
От полупрямой АВ в разные полуплоскости отложены
-
Даны три луча а,в,с с общей начальной точкой. Известно, что
-
Докажите, что если луч исходит из вершины угла и образует с его сторонами равные острые углы, то он является биссектрисой угла.
Задачи по теме «Смежные и вертикальные углы».
-
– вариант.
-
Найдите углы смежные с углами: а) 45⁰ б) 80⁰
-
Могут ли два смежных угла быть оба: а) тупыми б) прямыми
Объясните ответ.
-
Найдите смежные углы, если а) один из них на 20⁰ больше другого; б) один из них в 5 раз больше другого.
-
Какой угол образуют часовая и минутная стрелки часов, когда они показывают а) 5 часов б) 3 часа
-
Найдите смежные углы, если их градусные меры относятся как
1) 3:7 2) 11:25
6. Один из углов, которые получаются при пересечении двух прямых, равен
70⁰. Чему равны остальные углы.
7.Сумма двух углов, которые получаются при пересечении двух прямых, равна
40⁰. Найдите эти углы.
8. Один из углов, которые получаются при пересечении двух прямых, в 5 раза
больнее другого. Чему равны остальные углы.
-
Один из углов, которые получаются при пересечении двух прямых, на 40⁰ меньше другого. Найдите эти углы.
-
Найдите углы, которые получаются при пересечении двух прямых, если сумма трёх из них равна 260⁰.
-
Чему равен угол между биссектрисой и стороной данного угла, равного а) 52⁰ б) 132⁰
-
Найдите угол, если его биссектриса образует со стороной угол, равный а) 45⁰ б) 77⁰
-
Найдите угол между биссектрисой и продолжением одной из сторон данного угла, равного а) 50⁰ б) 150⁰
-
Из вершины развёрнутого угла АОС в одну полуплоскость проведены лучи ОК и ОР. Чему равен
-
Из вершины развёрнутого угла АОС в одну полуплоскость проведены лучи ОК и ОР. Чему равен
-
От полупрямой АВ в разные полуплоскости отложены
-
Даны три луча а,в,с с общей начальной точкой. Известно, что
-
Докажите, что если луч исходит из вершины угла и образует с его сторонами равные острые углы, то он является биссектрисой угла.







 Геометрия 7 класс. 1 вариант
Геометрия 7 класс. 1 вариант
 ва острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол.
ва острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол.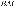 и на его биссектрисе
и на его биссектрисе  и
и 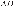 .
. равна 160°.
равна 160°. 
 проведены две
проведены две 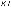 и
и 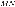 . На эти хорды опущены
. На эти хорды опущены 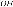 и
и 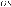 .
. 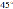 , то вертикальный с ним угол равен
, то вертикальный с ним угол равен 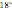 ?
? 5. Определите, сколько необходимо закупить пленки
5. Определите, сколько необходимо закупить пленки 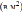 для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.
для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.  6. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в
6. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в 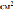 ) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно
) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно  еометрия 7 класс. Вариант 2
еометрия 7 класс. Вариант 2 .
.

















