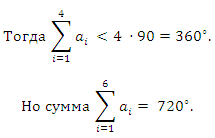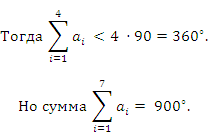Тесты по геометрии. 8 класс.

ТЕСТЫ ПО ГЕОМЕТРИИ 8 КЛАСС

№1 Многоугольники

 

Вариант 1

  1. Дан выпуклый десятиугольник А₁А₂...А₁₀. Сколько общих точек с прямой А₁А₂ имеет отрезок А₅А₃?

  1) 0

  2) 1

  3) бесконечно много

  4) нельзя определить

  Ответ: 1.

  2. Дан невыпуклый десятиугольник А₁А₂....А₁₀. Сколько общих точек с прямой А₁А₂ имеет отрезок А₃А₅?

  1) 0

  2) 1

  3) бесконечно много

  4) нельзя определить

  Ответ: 4.

  3. Дан выпуклый семиугольник А₁А₂...А₇. Сколько всего диагоналей выходят из его вершин А₁ и А₂?

  1) 14

  2) 10

  3) 8

  4) 7

  5) нельзя определить

  Ответ: 3.

  4. Найдите сумму всех углов выпуклого семнадцатиугольника А₁А₂...А₁₇.

  1) 6120°

  2) 360°

  3) 2700°

  4) 17000°

  5) нельзя определить

  Ответ: 3.

  5. Углы выпуклого четырёхугольника относятся как 2 : 3 : 7 : 6. Найдите величины этих углов.

  Ответ: 40°, 60°, 140°, 120°.

  6. Дан пятиугольник ABCDE, угол В = 40°, угол С = 60°, угол D = 140°, угол Е = 20°. Найдите величину угла А.

 

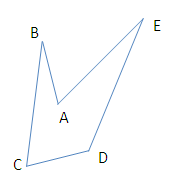
  Ответ: 280°.

  7. Какое наибольшее число острых углов может иметь выпуклый шестиугольник?

  Решение:

  Пусть a_i, i = 1, 2, ..., 6 углы выпуклого шестиугольника и a_i, i = 1, 2, 3, 4 - острые углы.

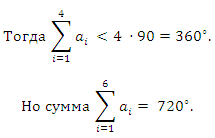
  Значит, a₅ + a₆  360° и значит, хотя бы один из этих углов больше развёрнутого. Поэтому четырёх острых углов быть не может. Приведём пример шестиугольника с тремя острыми углами: 60°, 75°, 170°, 170°, 170°, 75°.

  Ответ: 3.

Вариант 2

  1. Дан выпуклый двенадцатиугольник А₁А₂...А₁₂. Сколько общих точек с прямой А₃А₈ имеет ломаная А₄А₁₁...А₁₂?

  

  Ответ: 2.

  2. Дан невыпуклый двенадцатиугольник А₁А₂...А₁₂. Сколько общих точек с прямой А₃А₈ имеет ломаная А₄А₁₁А₁₂?

  

  Ответ: 4.

  3. Дан выпуклый восьмиугольник А₁А₂...А₈. Сколько всего диагоналей выходят из его вершин А₁ и А₅?

  1) 14

  2) 10

  3) 8

  4) 9

  5) нельзя определить

  Ответ: 4.

  4. Найдите сумму всех углов выпуклого восемнадцатиугольника А₁А₂...А₁₈.

  1) 2880°

  2) 360°

  3) 3240°

  4) 6480°

  5) нельзя определить

  Ответ: 1.

  5. Углы выпуклого четырёхугольника относятся как 1 : 4 : 6 : 7. Найдите величины этих углов.

  Ответ: 20°, 80°, 120°, 140°.

  6. Дан пятиугольник ABCDE, угол В = 40°, угол С = 20°, угол D = 190°, угол Е = 30°. Найдите величину угла А.

 

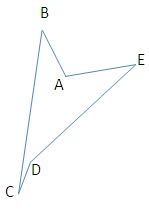
  Ответ: 260°.

  7. Какое наибольшее число острых углов может иметь выпуклый семиугольник?

  Решение:

  Пусть a_i, i = 1, 2, ..., 7 углы выпуклого семиугольника и a_i, i = 1, 2, 3, 4 - острые углы.

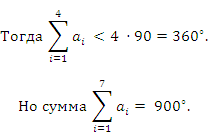
  Значит, а₅ + а₆ + а₇  540° и значит, хотя бы один из этих углов больше развёрнутого. Поэтому четырёх острых углов быть не может. Приведём пример семиугольника с тремя острыми углами: 50°, 75°, 175°, 175°, 175°, 175°, 75°.

  Ответ: 3.

№2 Определение, свойства сторон и углов параллелограмма

 

Вариант 1

  1. Из приведённых предложений выберите определение параллелограмма

  Ответ: 2.

  2. В параллелограмме ABCD угол А = 128°. Найдите углы В и С.

  1) В = 128°, С = 128°

  2) В = 128°, С = 52°

  3) В = 52°, С = 128°

  4) В = 52°, С = 52°

  5) невозможно найти

  Ответ: 3.

  3. В параллелограмме ABCD угол А = 11· угол В. Найдите угол С.

  1) 10

  2) 15

  3) 110

  4) 165

  5) невозможно найти

  Ответ: 4.

  4. В параллелограмме ABCD АВ = 12, а периметр 80. Найдите сторону ВС.

  1) 28

  2) 38

  3) 34

  4) 12

  5) невозможно найти

  Ответ: 1.

  5. Периметр параллелограмма ABCD равен 34. Периметр треугольника АВС равен 25. Найдите длину диагонали АС параллелограмма ABCD.

  Ответ: 8.

  6. Угол между диагоналями параллелограмма ABCD равен 60°, угол САВ = 20°. Найдите величину угла ВСD, если известно, что он тупой.

  Ответ: 100°.

  7. В параллелограмме ABCD угол А равен 60°, ВС = 10, BD перпендикулярна АВ. Найдите периметр параллелограмма.

  Ответ: 30.

  8. В плоском четырёхугольнике две противоположные стороны равны между собой, а две другие стороны параллельны. Будет ли этот четырёхугольник параллелограммом? Ответ следует обосновать.

  Ответ: Нет, этим свойством обладает трапеция с равными боковыми сторонами.

Вариант 2

  1. Из приведённых предложений выберите те, которые не являются определением параллелограмма

  1) Параллелограмм - четырёхугольник на плоскости, у которого противоположные стороны попарно равны.

  2) Параллелограмм - четырёхугольник на плоскости, у которого противоположные стороны попарно параллельны.

  3) Если пара параллельных прямых пересекает другую пару параллельных прямых, то полученный в результате четырёхугольник - параллелограмм.

  4) Если у плоского четырёхугольника противоположные углы попарно равны, противоположные стороны попарно равны и диагонали точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм.

  Ответ: 1, 3, 4.

  2. В параллелограмме ABCD угол В = 81°. Найдите углы А и С.

  1) А = 99°, С = 99°

  2) А = 81°, С = 81°

  3) А = 81°, С = 99°

  4) А = 99°, С = 81°

  5) невозможно найти

  Ответ: 1.

  3. В параллелограмме ABCD угол А · 5 = угол В. Найдите угол D.

  1) 30°

  2) 60°

  3) 120°

  4) 150°

  5) невозможно найти

  Ответ: 4.

  4. В параллелограмме ABCD АВ = 40, а периметр 100. Найдите сторону ВС.

  1) 60

  2) 50

  3) 40

  4) 10

  5) невозможно найти

  Ответ: 4.

  5. Периметр параллелограмма ABCD равен 78. Периметр треугольника АВС равен 46. Найдите длину диагонали АС параллелограмма ABCD.

  Ответ: 7.

  6. Угол между диагоналями параллелограмма ABCD равен 30°, угол САВ = 10°. Найдите величину угла BDC, если известно, что он тупой.

  Ответ: 140°.

  7. В параллелограмме ABCD угол А равен 60°, ВС = 40, BD перпендикулярна CD. Найдите периметр параллелограмма.

  Ответ: 120.

  8. В плоском четырёхугольнике противоположные углы попарно равны. Будет ли этот четырёхугольник параллелограммом? Ответ следует обосновать.

  Ответ: Будет.

№3 Свойства высот и биссектрис углов параллелограмма

 

Вариант 1

  1. В параллелограмме ABCD прямая, содержащая высоту, проведённую из вершины острого угла А, образует с прямой DC угол, равный 12°. Найдите угол В.

  1) 12

  2) 24

  3) 68

  4) 102

  5) невозможно найти

  Ответ: 4.

  2. В параллелограмме ABCD прямая, содержащая биссектрису угла А, образует с прямой ВС угол, равный 10°. Найдите угол D.

  1) 100°

  2) 150°

  3) 120°

  4) 160°

  5) невозможно найти

  Ответ: 4.

  3. В параллелограмме ABCD АВ = 12. Найдите расстояние от середины CD до точки пересечения биссектрис углов С и D.

  1) 6

  2) 12

  3) 24

  4) 36

  5) невозможно найти

  Ответ: 1.

  4. В параллелограмме ABCD угол А равен 65°. Отрезки СС₁ и СС₂ - его высоты. Найдите величину угла С₁СС₂.

  1) 135°

  2) 125°

  3) 115°

  4) 165°

  5) невозможно найти

  Ответ: 3.

  5. В параллелограмме ABCD отрезок ВК - биссектриса угла В и точка К лежит на стороне AD, причём АК = 7, KD = 23. Найдите периметр параллелограмма ABCD.

  1) 30

  2) 74

  3) 90

  4) 126

  5) невозможно найти

  Ответ: 2.

  6. Докажите, что точки пересечения всех четырёх биссектрис параллелограмма являются вершинами прямоугольника.

  7. Биссектрисы углов А и D параллелограмма ABCD делят сторону ВС на три части, отношение которых, считая от точки В, равно 2 : 3 : 2. Найдите длины сторон параллелограмма, если его полупериметр равен 216.

  Ответ: 90, 90, 126, 126 или 48, 48, 168, 168.

 

Вариант 2

  1. В параллелограмме ABCD прямая, содержащая высоту, проведённую из вершины острого угла А, образует с прямой ВС угол, равный 21°. Найдите угол D.

  1) 111°

  2) 121°

  3) 21°

  4) 159°

  5) невозможно найти

  Ответ: 1.

  2. В параллелограмме ABCD прямая, содержащая биссектрису угла В, образует с прямой CD угол, равный 40°. Найдите угол А.

  1) 21°

  2) 59°

  3) 100°

  4) 159°

  5) невозможно найти

  Ответ: 3.

  3. В параллелограмме ABCD ВС = 50. Найдите расстояние от середины AD до точки пересечения биссектрис углов А и D.

  1) 10

  2) 20

  3) 25

  4) 50

  5) невозможно найти

  Ответ: 3.

  4. В параллелограмме ABCD высоты СС₁ и СС₂, причём угол С₁СС₂ = 70°. Найдите величину угла D.

  1) 20°

  2) 70°

  3) 110°

  4) 160°

  5) невозможно найти

  Ответ: 2.

  5. В параллелограмме ABCD отрезок ВК - биссектриса угла В, точка К лежит на стороне AD, причём АК = 17, KD = 33. Найдите периметр параллелограмма ABCD.

  1) 100

  2) 117

  3) 132

  4) 134

  5) невозможно найти

  Ответ: 4.

  6. В параллелограмме ABCD на сторонах ВС и AD отложены равные отрезки BF и DE соответственно. Отрезки AF и ВЕ пересекаются в точке М, отрезки DF и СЕ пересекаются в точке L. Докажите, что MELF - параллелограмм.

  7. Биссектрисы углов А и D параллелограмма ABCD делят сторону ВС на три части, отношение которых, считая от точки В, равно 4 : 3 : 4. Найдите длины сторон параллелограмма, если его полупериметр равен 270.

  Ответ: 72, 72, 198, 198 или 105, 105, 165, 165.

№4 Ромб, квадрат, прямоугольник  Вариант1 

  

  4. В прямоугольнике ABCD биссектриса угла А пересекает сторону ВС в её середине - точке М и сторона AD = 120. Найдите периметр прямоугольника ABCD.

  1) 480

  2) 300

  3) 360

  4) 720

  5) невозможно найти

  Ответ: 3.

  5. В квадрате ABCD проведены биссектрисы углов ВАС и DAC, пересекающие стороны ВС и CD квадрата в точках М и L соответственно. Найдите наибольший угол треугольника AML.

  1) 167,5°

  2) 135°

  3) 75°

  4) 67,5°

  5) невозможно найти

  Ответ: 4.

 

  7. В прямоугольнике ABCD биссектриса угла С делит сторону AD в отношении 2 : 5. Найдите отношение длин сторон.

  Ответ: 2 : 7 или 5 : 7.

Вариант 2

  2. Диагональ ромба образует с его стороной угол, равный 58°. Найдите острый угол ромба.

  1) 32

  2) 64

  3) 72

  4) 84

  5) невозможно найти

  Ответ: 2.

  3. В ромбе ABCD угол А = 120°, BD = 32 и диагонали пересекаются в точке О. Найдите расстояние от точки О до стороны ВС.

  1) 8

  2) 16

  3) 10

  4) 24

  5) невозможно найти

  Ответ: 1.

  4. В прямоугольнике ABCD биссектриса угла В пересекает сторону AD в её середине - точке М и сторона CD = 20. Найдите периметр прямоугольника ABCD.

  1) 160

  2) 100

  3) 80

  4) 120

  5) невозможно найти

  Ответ: 4.

  5. В квадрате ABCD проведены биссектриса угла ВАС, пересекающая сторону ВС в точке М. Найдите больший угол треугольника АМС.

  1) 67,5°

  2) 125°

  3) 65°

  4) 112,5°

  5) невозможно найти

  Ответ: 4.

  6. В ромбе ABCD угол А = 120°, BD = 32. Найдите высоты ромба.

  Ответ: 16, 16.

  7. В прямоугольнике ABCD биссектриса угла С делит сторону AD в отношении 3 : 7. Найдите отношение сторон этого прямоугольника.

  Ответ: 3 : 10 или 7 : 10.

  8. На сторонах ВС и CD квадрата ABCD отмечены точки Р и Т так, что ВТ = АР и отрезки ВТ и АР пересекаются в точке О. Найдите угол ТОР.

  Ответ: 90°.

№5 Трапеция 

Вариант 1

  1. В равнобедренной трапеции ABCD основания ВС = 2 см и AD = 20 см. Из вершины В на основание AD опущена высота ВН. Найдите HD.

  1) 10

  2) 8

  3) 11

  4) 9

  5) невозможно найти

  Ответ: 3.

  2. В прямоугольной трапеции ABCD (угол А прямой) основание ВС вдвое меньше AD и диагональ АС = 1 см. Найдите боковую сторону CD трапеции ABCD.

  1) 1

  2) 2

  3) 3

  4) 4

  5) невозможно найти

  Ответ: 1.

  3. В трапеции ABCD основания ВС, AD, диагональ BD = 18 см, угол BAD = 60° и боковая сторона АВ перпендикулярна диагонали BD. Найдите высоту трапеции.

  1) 3

  2) 9

  3) 6

  4) 12

  5) невозможно найти

  Ответ: 2.

  4. В трапеции ABCD, ВС и AD - параллельны, угол BAD = 20°, угол CDA = 70°. Найдите угол между прямыми АВ и CD.

  1) 40°

  2) 60°

  3) 80°

  4) 90°

  5) невозможно найти

  Ответ: 4.

  5. В трапеции ABCD перпендикуляр, проходящий через середину Н боковой стороны CD пересекает основание AD в его середине - точке О. Найдите угол ACD.

  Ответ: 90°.

  6. В трапеции ABCD, ВС и AD - параллельны, угол BAD = 40°. Диагональ АС трапеции делит её на два равнобедренных треугольника. Найдите углы трапеции.

  Ответ: 20°, 40°, 140°, 160° или 40°, 80°, 100°, 140°.

 

Вариант 2

  

  1) 11

  2) 14

  3) 18

  4) 21

  5) невозможно найти

  Ответ: 4.

  

  1) 5

  2) 10

  3) 20

  4) 8

  5) невозможно найти

  Ответ: 2.

  1) 4

  2) 7

  3) 14

  4) 21

  5) невозможно найти

  Ответ: 3.

 

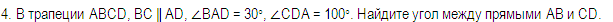
  1) 50°

  2) 60°

  3) 70°

  4) 90°

  5) невозможно найти

  Ответ: 1.

  Ответ: 10.

  

  Ответ: 40°, 80°, 100°, 140° или 70°, 80°, 100°, 110°.

№ 6 Средняя линия треугольника и трапеции

теорема Фалеса

теорема о пропорциональных отрезках

 

Вариант 1

  1. В треугольнике АВС, ВС = 36 см. Через точку М, которая делит сторону АС так, что АМ : МС = 5 : 7, проведена прямая ML параллельно прямой АВ, пересекающая ВС в точке L. Найдите LC.

  1) 11

  2) 18

  3) 20

  4) 21

  5) невозможно найти

  Ответ: 4.

  2. Боковая сторона AD трапеции ABCD равна 51 см. Через точку М, которая делит боковую сторону ВС так, что ВМ : МС = 11 : 6, проведена прямая MN параллельно основанию АВ, пересекающая AD в точке N. Найдите AN.

  1) 33

  2) 22

  3) 11

  4) 6

  5) невозможно найти

  Ответ: 1.

  3. Диагонали четырёхугольника равны 120 см и 248 см. Найдите периметр четырёхугольника, вершинами которого являются середины сторон данного четырёхугольника.

  1) 240

  2) 368

  3) 496

  4) 128

  5) невозможно найти

  Ответ: 2.

  4. Дан произвольный четырёхугольник АВМТ (никакие пары противоположных сторон не параллельны). Точки L и Н - середины отрезков АМ и МВ. Точки G и Y - середины отрезков АТ и ВТ. Найдите периметр четырёхугольника LHYG, если АВ + МТ = 20.

  1) 40

  2) 30

  3) 20

  4) 10

  5) невозможно найти

  Ответ: 3.

  5. В трапеции ABCD на боковой стороне CD отмечена точка Н так, что СН : HD = 2 : 5. Прямая HG, параллельная основаниям ВС и AD, пересекает сторону АВ в точке G. Найдите GH, если ВС = 14, AD = 21.

  Ответ: 16.

  6. В треугольнике АВС на стороне ВС отмечена точка D так, что CD : DB = 1 : 2. В каком отношении прямая, проходящая через точку В и середину отрезка AD делит сторону АС, считая от точки А.

  Ответ: 2 : 3.

 

Вариант 2

  1) 10

  2) 25

  3) 20

  4) 35

  Ответ: 4.

  1) 18

  2) 28

  3) 38

  4) 9

  Ответ: 1.

  1) 640

  2) 388

  3) 136

  4) 252

  Ответ: 2.

  1) 10

  2) 20

  3) 30

  4) 40

  Ответ: 3.

  Ответ: 30.

  Ответ: 7 : 4.

№7 Центральная и осевая симметрия

Вариант 1

  1. Укажите фигуры, из предложенных на рисунке, которые имеют центр симметрии. (Фигуры: равносторонний треугольник, равнобокая трапеция, окружность, параллелограмм, равнобедренный прямоугольный треугольник.)

  1) 1

  2) 2

  3) 3

  4) 4

  5) 5

  Ответ: 3, 4.

  2. Укажите фигуру, из предложенных на рисунке, которая имеет наибольшее число осей симметрии. (Фигуры: равносторонний треугольник, звезда, крест, ромб, равнобедренный прямоугольный треугольник.)

  1) 1

  2) 2

  3) 3

  4) 4

  5) 5

  Ответ: 2.

  3. Длина отрезка ВС = 14 см. Этот отрезок центрально симметрично отобразили относительно точки О, лежащей на отрезке ВС так, что ВС : ОС = 3 : 4. Пусть точка В₁ центрально симметрична точке В. Найдите длину отрезка В₁С.

  1) 1   2) 2   3) 3   4) 4   5) 5

  Ответ: 3.

  4. В треугольнике АВС, угол В = 40°, угол С = 70°, проведена высота AD. Пусть точка С₁ симметрична точке С относительно прямой AD. Найдите угол ВАС₁.

  1) 30°

  2) 70°

  3) 40°

  4) 140°

  5) не определен

  Ответ: 1.

  5. В треугольнике АВС на стороне ВС отмечена точка О. При симметрии относительно точки О точки А, В и С переходят соответственно в точки А₁, В₁ и С₁. Докажите, что четырёхугольник АСА₁С₁ - параллелограмм.

  6. Нарисуйте фигуру, имеющую ровно 7 осей симметрии.

Вариант 2

 

  1) 1   2) 2   3) 3   4) 4   5) 5

  Ответ: 1.

 

 

  

  Ответ: 5.

  1) 12

  2) 22,5

  3) 30

  4) 17,5

  5) 40

  Ответ: 3.

  1) 110°

  2) 70°

  3) 40°

  4) 140°

  Ответ: 2.

  

№ 8 Площадь 

  1) 8

  2) 10

  3) 14

  4) 24

  5) 7

  Ответ: 2.

  2. В прямоугольнике площадью 120 см², проведена диагональ. Найдите площадь треугольника, две вершины которого совпадают с двумя соседними вершинами прямоугольника, а третья вершина - середина проведённой диагонали.

  1) 10

  2) 40

  3) 30

  4) 50

  Ответ: 3.

  3. Прямоугольник разделён прямыми, параллельными его сторонам на шесть прямоугольников, площади четырёх из которых указаны на рисунке. Найдите площадь данного прямоугольника.

 

  1) 125

  2) 130

  3) 120

  4) 115

  Ответ: 1.

  4. Через середину М стороны АВ треугольника АВС и через точку L стороны АС, AL : LC = 2 : 5, проведена прямая ML. Определите, во сколько раз площадь треугольника AML меньше площади четырёхугольника BCML.

  1) 10

  2) 2

  3) 6

  4) 9

  5) 5

  Ответ: 3.

  5. Через середину стороны параллелограмма и через вершину, не принадлежащую этой стороне, проведена прямая, отсекающая от параллелограмма треугольник площадью, равной 4. Найдите площадь параллелограмма.

  1) 20

  2) 8

  3) 12

  4) 16

  Ответ: 4.

  6. Высота равнобокой трапеции, равная 6 и опущенная из вершины на большее основание, делит его на два отрезка, больший из которых равен 10. Найдите площадь этой трапеции.

  1) 42

  2) 60

  3) 36

  4) 80

  Ответ: 2.

  7. Две стороны параллелограмма равны 10 см и 12 см, а одна из высот равна 6 см. Найдите вторую высоту параллелограмма.

  Ответ: 5 см или 7,2 см.

  8. Острый угол параллелограмма равен 30°, а высоты равны 10 см и 20 см. Найдите площадь параллелограмма.

  Ответ: 400 см².

  Ответ: 58 см².

№ 9 Теорема Пифагора

обратная теорема Пифагора

 

Вариант 1

  1. В прямоугольном треугольнике АВС угол С - прямой, АВ = 20, ВС = 12. Найдите АС.

  1) 14

  2) 16

  3) 18

  4) 4√34

  Ответ: 2.

  2. В прямоугольном треугольнике АВС угол С - прямой, АВ = 26, катеты относятся как 5 : 12. Найдите больший катет.

  1) 12

  2) 16

  3) 18

  4) 24

  Ответ: 4.

  3. В треугольнике АВС ВН - высота. АВ = 17, ВН = 15. Найдите АН.

  1) 2

  2) 6

  3) 8

  4) 12

  Ответ: 3.

  4. В треугольнике АВС АВ = 7, ВС = 24, АС = 25. Выберите верное утверждение:

  1) угол А прямой

  2) угол В прямой

  3) угол С прямой

  4) треугольник АВС не является прямоугольным

  Ответ: 2.

  5. Найдите сторону квадрата с диагональю 4√2.

  Ответ: 4.

  6. Одна из диагоналей прямоугольника равна 17, а одна из сторон равна 8. Найдите периметр прямоугольника.

  Ответ: 46.

  7. В трапеции ABCD CD = 7,5; ВС = 4; AD = 8,5. Углы А и В прямые. Найдите АВ.

  Ответ: 6.

  8. В треугольнике АВС АВ = 13; ВС = 14; АС = 15. Найдите высоту АН.

  Ответ: 12.

 

Вариант 2

  

  3. В равнобедренном треугольнике АВС ВН - медиана. АВ = ВС = 13, АС = 10. Найдите ВН.

  1) 2

  2) 6

  3) 12

  4) 16

  Ответ: 3.

  

  5. Найдите сторону ромба с диагоналями 5 и 12.

  Ответ: 6,5.

  7. В четырёхугольнике ABCD АВ = 13, ВС = 14, АС = 15. Углы А и В прямые. Найдите CD.

  Ответ: 7,5.

  

№10 Подобные треугольники

 

Вариант 1

  

  2. В треугольнике АВС, АВ = 12, ВС = 9. Отрезок MN параллелен ВС, причем точка М лежит на стороне АВ, точка N лежит на стороне АС, АМ = 3. Найдите MN.

  1) 2

  2) 2,25

  3) 2,5

  4) 6

  5) 7

  Ответ: 2.

  3. В трапеции ABCD (BC и AD - параллельны) диагонали пересекаются в точке О. Площадь треугольника ВОС равна 3, а площадь треугольника AOD равна 27. Найдите АС, если АО = 6.

  1) 2

  2) 6

  3) 8

  4) 12

  Ответ: 3.

  4. В треугольнике АВС на стороне АВ взяли точку К, а на стороне ВС взяли точку N так, что угол BAN = углу ВСК. АК = 0,5; КВ = 7,5; BN = 5. Найдите NC.

  1) 7,5

  2) 5

  3) 1,5

  4) 7

  Ответ: 4.

  5. В треугольнике АВС на стороне АВ взяли точку К, а на стороне ВС взяли точку N так, что АК : КВ = CN : NB = 2 : 1. Во сколько раз площадь четырехугольника AKNC больше площади треугольника KBN?

  Ответ: в 8 раз.

  6. В треугольнике АВС на стороне АС выбрали точку D так, что угол В + угол BDC = 180°. Докажите, что АВ² = АС · AD.

  8. В треугольнике АВС на стороне ВС выбраны точки N и К так, что угол BAN = углу АСВ, угол САК = углу АВС. BN = 1, KC = 4. Найдите AN.

  Ответ: 2.

№11 Пропорциональные отрезки в прямоугольном треугольнике

 

Вариант 1

  1. Вычислите высоту прямоугольного треугольника, проведенную к гипотенузе, если его катеты равны 3 и 4.

  1) 2

  2) 2,4

  3) 2,5

  4) 3

  5) 4

  Ответ: 2.

  2. В прямоугольном треугольнике АВС угол С прямой, СН - высота, АВ = 15, АН = 3. Найдите СН.

  1) 5

  2) 6

  3) 7

  4) 8

  5) 9

  Ответ: 2.

  3. В прямоугольном треугольнике АВС угол С прямой, СН - высота. Найдите АН, если АН : НВ = 1 : 8, АС = 9.

  1) 1,5

  2) 2

  3) 3

  4) 6

  Ответ: 3.

  4. Высота прямоугольного треугольника равна 6, а проекция одного из катетов на гипотенузу равна 12. Найдите гипотенузу.

  1) 12

  2) 15

  3) 18

  4) 21

  5) 24

  Ответ: 2.

  5. Сторона ромба равна 10, а одна из диагоналей 16. Найдите расстояние от центра ромба до его стороны.

  Ответ: 4,8.

  6. Биссектрисы углов при боковой стороне АВ трапеции ABCD пересекаются в точке К. Найдите расстояние от точки К до прямой АВ, если АК = √3, АВ = 2.

  Ответ: √3/2.

  7. В прямоугольном треугольнике отношение катетов равно 1 : 2. Найдите отношение проекций этих катетов на гипотенузу.

  Ответ: 1 : 4.

  8. Дан прямоугольник ABCD. АВ : AD = 1 : 3. АН - высота треугольника BAD. Площадь треугольника АВН равна 1. Найдите площадь ABCD.

  Ответ: 20.

№12 Практические задачи на подобие

 

Вариант 1

  1. Длина тени, отбрасываемой тридцатисантиметровой линейкой, равна 15 см. Чему равна высота столба в метрах, если отбрасываемая им тень составляет 3 м?

  1) 3

  2) 4

  3) 5

  4) 6

  Ответ: 4.

  2. Вычисление недоступного расстояния. На рисунке отмечены измеренные расстояния CD, MD, AM, угол MCD = углу МВА. Найдите АВ в метрах.

  1) 270

  2) 130

  3) 100

  4) 300

  Ответ: 1.

  3. Вычислите глубину колодца (расстояние до воды в метрах) по размерам, заданным на рисунке. АО = 10 см, ОВ = 90 см. Найти ВН.

 

  1) 2

  2) 4,5

  3) 4

  4) 1,5

  Ответ: 2.

  4. Дан прямоугольный лист бумаги размерами 120 мм и 240 мм. Требуется определить площадь (в квадратных сантиметрах) подобного ему прямоугольника, полученного с помощью одного разреза данного прямоугольника.

  1) 24

  2) 56

  3) 72

  4) 108

  Ответ: 3.

№13 Значения синуса, косинуса и тангенса некоторых углов

 

Вариант 1

  1. Найдите sin 45°.

  Ответ: √2/2.

  2. Найдите cos 30°.

  Ответ: √3/2.

  3. Найдите tg 60°.

  Ответ: √3.

  4. Найдите sin α, если cos α = 0,8.

  1) 0,8   2) 0,2   3) 0,6   4) 0,64   5) 0,36

  Ответ: 3.

  5. Найдите синус угла А треугольника АВС, если угол С = 90°, а косинус угла В равен 0,4.

  Ответ: 0,4.

  6. Вычислите 4sin 30° ctg 45° − 8sin 60° tg 30°.

  Ответ: −2.

  7. Вычислите 10√3 cos 60° ctg 60° − 12√2 sin 45° tg 45°.

  Ответ: −7.

 

Вариант 2

  1. Найдите sin 60°.

  Ответ: √3/2.

  2. Найдите cos 45°.

  Ответ: √2/2.

  3. Найдите tg 30°.

  Ответ: √3/3.

  4. Найдите sin α, если cos α = 0,6.

  1) 0,2   2) 0,4   3) 0,6   4) 0,8

  Ответ: 1.

  5. Найдите косинус угла А треугольника АВС, если угол С = 90°, а синус угла В равен 0,35.

  Ответ: 0,35.

  6. Вычислите √6 sin 60° cos 45° + √3 tg 30°.

  Ответ: 2,5.

  7. Вычислите √12 cos 30° (cos 60° − ctg 45°).

  Ответ: −1,5.

№14 Тригонометрические функции острого угла и соотношения между ними

 

Вариант 1

  1. Дан прямоугольный треугольник FDC, угол С = 90°, sin F = 0,64. Найдите cos D.

  1) 0,64

  2) 0,36

  3) 0,5

  4) 1

  Ответ: 1.

 

  2. В равнобедренном треугольнике АВС АВ = ВС = 10, АС = 5. Найдите cos A.

  

  3. В прямоугольном Δ АВС угол С прямой, СН - высота, АВ = 15, cos А = 0,6. Найти АН.

  

  4. Диагонали ромба равны 3 и 4. Найдите синус угла между большей диагональю и стороной ромба.

  

  5. Вычислите sin² 30° + sin² 40° + sin² 50°.

  

  7. Через вершину С треугольника АВС проведена прямая CD, параллельная АВ, причем А и D лежат по разные стороны от прямой ВС. DH - высота в треугольнике BCD. АС = 8, ВС = 6, АВ = 10. Вычислите cos угла CDH.

  Ответ: 0,8.

  8. Найдите косинус угла при вершине равнобедренного Δ, если высота проведенная к боковой стороне меньше этой стороны в 3 раза.

  

  9. Докажите, что сумма синусов острых углов прямоугольного Δ не превосходит √2.

  Доказательство:

  Пусть sin A + sin B = α, тогда sin A + cos A = α 0 и α² − 1 = sin2A ≤ 1.

  Следовательно, а² ≤ 2 ↔ 0

№15 Пропорциональные отрезки в круге

 

Вариант 1

  1. В окружности две хорды пересекаются, образуя четыре отрезка. Три из них имеют длину 2, 3, 6. Найдите длину четвертого, если он длиннее всех остальных.

  1) 7,5

  2) 8

  3) 9

  4) 12

  5) 18

  Ответ: 3.

  2. Из точки А, лежащей вне круга, проведены две его секущие. Первая пересекает окружность круга в точках В и С, вторая - в точках D и Е, причём АВ = 2, ВС = 4, АЕ = 12. Найдите AD, если В лежит между А и С, а D между А и Е.

  

  3. Из точки А, лежащей на расстоянии 25 от центра окружности радиуса 15, проведена касательная, точка Р - точка касания. Найдите АР.

  1) 10

  2) 20

  3) 30

  4) 40

  5) 50

  Ответ: 2.

  4. В окружности хорда АВ и диаметр CD пересекаются в точке К, причем АВ перпендикулярно CD. Найдите АВ, если СК = 1, а CD = 10.

  1) 5

  2) 7

  3) 11

  4) 6

  5) 9

  Ответ: 4.

  5. Окружность проходит через вершины А и В прямоугольника ABCD, и пересекает его стороны ВС и AD в точках К и М соответственно. Из точки С проведена касательная к окружности СР. Найдите СР, если АВ = 6, ВС = 9, а радиус окружности равен 5.

  Ответ: 3.

  6. Из точки М к окружности проведены касательная МС и секущая АВ (точка В лежит между А и М). Найдите МВ, если МС = 2√2, АВ = 2.

  Ответ: 2.

  7. Докажите, что если в окружности две хорды делятся точкой пересечения в одном и том же отношении, то они равны.

№16 Окружность и касательная к окружности

 

Вариант 1

  1. Даны прямая и окружность радиуса 5. Дано расстояние d от центра окружности до прямой. Определите взаимное расположение прямой и окружности при d = 10, d = 5, d = 0, d = 4.

 

 

  2. Из точки А проведены две касательные к окружности, причем В и С - точки касания, О - центр. Найдите угол ВАС, если угол ВОС равен 115°.

  1) 115°   2) 90°   3) 55°   4) 65°   5) 75°

  Ответ: 4.

 

  3. Из точки А к окружности с центром О проведены касательные АВ и АС, В и С - точки касания. Оказалось, что А и О симметричны относительно ВС. Найдите угол ВАС.

   

 

  5. Из точки А к окружности с центром О проведены касательные АВ и АС, В и С - точки касания; угол АОВ = 8 · угол ОАС. Найдите угол ВОС.

  Ответ: 160°.

 

  6. Радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 2. Как расположены эти окружности?

  Ответ: Окружности касаются внутренним образом.

 

  

 

  8. Дан прямоугольный треугольник с катетом 5 и гипотенузой 13. Найдите максимальный возможный радиус окружности с центром в вершине прямого угла, имеющей общие точки с гипотенузой треугольника.

  Ответ: 12.

№17 Центральные и вписанные углы

 

Вариант 1

  

 

  2. Дана окружность. Центральный угол АОВ равен 110°. Найдите вписанный угол ВСА, если отрезки АВ и ОС пересекаются.

  1) 55°     2) 90°     3) 110°     4) 125°     5) 70°

  Ответ: 4.

 

  

 

  4. Хорды АВ и CD окружности пересекаются в точке К, причем АВ = 8, СК = 3, DK = 4. Найти АК, если известно, что АК ВК.

  1) 3     2) 4     3) 5     4) 6

  Ответ: 4.

 

  5. Хорда АВ окружности с центром О перпендикулярна ее радиусу ОС и делит его на отрезки ОК = 1,5 и СК = 1. Найдите длину хорды АВ.

  Ответ: 4.

 

  6. Найдите больший из углов, образованных касательной к окружности в точке А и хордой АВ, равной радиусу окружности.

  Ответ: 150°.

 

  7. Точка А лежит вне круга, ограниченного окружностью w. Угол с вершиной А высекает на окружности w дуги градусной меры 40° и 88°. Найдите величину угла А.

  Ответ: 24°.

 

  8. Хорды АВ и CD окружности пересекаются в точке К. Найдите угол AKD, если сумма градусных мер дуг AD и ВС равна сумме градусных мер дуг DB и АС.

  Ответ: 90°.

№18 Замечательные точки треугольника

вписанная и описанная окружности треугольника

 

Вариант 1

  1. Определите положение центра описанной окружности, если наибольший угол треугольника равен: А. 75°, Б. 90°, В. 100°, Г. 58°.

  1) Лежит вне треугольника

  2) Лежит внутри треугольника

  3) Лежит на стороне треугольника

  4) Недостаточно данных

  5) Такого треугольника не существует

  Ответ: 1 - В, 2 - А, 3 - Б, 5 - Г.

 

  2. Медианы AD и СЕ треугольника АВС пересекаются в точке М. Найдите AD + СЕ, если АМ + СМ = 8.

  1) 8     2) 9     3) 10     4) 11     5) 12

  Ответ: 5.

 

  3. Центр вписанной в треугольник окружности находится в точке пересечения его (выберите верное утверждение):

  1) высот

  2) биссектрис

  3) серединных перпендикуляров

  4) медиан

  5) нельзя определить

  Ответ: 2.

 

  4. Центр описанной около треугольника окружности (выберите верное утверждение):

  1) равноудален от его сторон

  2) лежит на его средней линии

  3) равноудален от его вершин

  4) делит медианы в отношении 2 : 1 считая от вершины

  5) лежит на пересечении высот Δ

  Ответ: 3.

 

  5. Катеты СВ и СА прямоугольного треугольника АВС равны 9 и 12 соответственно. М - точка пересечения медиан. Найдите длину отрезка СМ.

  Ответ: 5.

 

  6. Найдите радиус окружности, описанной около треугольника АВС, стороны которого равны 10, 10 и 12.

  Ответ: 6,25.

 

  

 

  8. Найдите расстояние от точки пересечения высот равнобедренного треугольника до его основания, если один из углов треугольника равен 120°, а боковая сторона равна 1.

  Ответ: 1,5.

№19 Вписанные и описанные четырехугольники

 

Вариант 1

  1. Четырехугольник ABCD вписан в окружность. Определите возможный вид четырехугольника ABCD.

  1) Ромб с острым углом 80°.

  2) Прямоугольная трапеция.

  3) Параллелограмм с углом 110°.

  4) Равнобокая трапеция.

  5) Четырехугольник с углом 210°.

  Ответ: 4.

 

  2. Средняя линия трапеции, описанной около окружности равна 5. Боковая сторона равна 6. Найдите вторую боковую сторону.

  1) 3     2) 4     3) 5      4) 6      5) 7

  Ответ: 2.

 

  3. Выберите верное утверждение:

  1) Все стороны четырехугольника, в который можно вписать окружность, равны между собой.

  2) Биссектрисы четырехугольника, в который можно вписать окружность, пересекаются в одной точке.

  3) Все углы четырехугольника, в который можно вписать окружность, равны между собой.

  4) Диагонали четырехугольника, вписанного в окружность, равны между собой.

  5) Нет верных утверждений.

  Ответ: 2.

 

  

 

  5. В треугольник АВС вписана окружность, и к ней проведена касательная, пересекающая сторону АВ в точке К, а сторону ВС в точке М. Известно, что АК = 3, КМ = 2, МС = 4. Найдите периметр четырехугольника АКМС.

  Ответ: 14.

 

  6. Найдите периметр прямоугольника, вписанного в окружность, радиуса 13, если одна из его сторон равна 10.

  Ответ: 68.

 

  7. Окружность, проходящая через вершины В и С треугольника АВС, пересекает сторону ВА в точке Р, а сторону СА в точке Q. Известно, что угол АРО = 40°, угол АВС = 75°. Найдите угол А.

  Ответ: 65°.

 

  8. В трапецию ABCD (ВС и AD - параллельны) можно вписать окружность. Точка М лежит на стороне АВ, а N лежит на стороне CD. Можно ли вписать окружность в четырехугольник AMND? Ответ обоснуйте.

  Ответ: нельзя.

  Решение: Пусть в четырёхугольник AMND вписана окружность. Тогда, по теореме, AD + MN = AM + ND. Из условия следует, что AD + BC = AB + CD. Вычтем из второго равенства первое. Получим, что BC − MN = BM + CN или ВС = ВМ + MN + NC. Но последнее равенство невозможно, т.к. ВМ + MN + NC BN + NC BC (по неравенству треугольника). Противоречие.

ИТОГОВЫЙ ТЕСТ ПО ГЕОМЕТРИИ

 

   На выполнение данного теста отводится 120 минут.

 

  1. Биссектриса острого угла А параллелограмма ABCD пересекает сторону ВС в точке М, которая делит ВС на два отрезка 8 см и 12 см. Прямая АМ пересекает продолжение стороны CD в точке F. Найдите длину отрезка DF.

  1) 24     2) 16      3) 20       4) 40

  Ответ: 3.

 

  2. Угол между высотами ромба ABCD, опущенными из вершины В, равен 123°. Найдите острый угол ромба.

  1) 83°     2) 27°     3) 57°     4) 23°

  Ответ: 3.

 

  

 

  4. Периметр ромба ABCD равен 40, периметр треугольника ABD равен 32. Найдите периметр треугольника АВС.

  1) 26     2) 28     3) 32     4) 36

  Ответ: 4.

 

  

 

  6. В треугольнике АВС, АВ = 12, АС = 16, ВС = 10 вписана окружность, касающаяся стороны АС в точке В₁. Найдите АВ₁.

  1) 9     2) 10     3) 2     4) 4

  Ответ: 1.

 

  7. В треугольнике АВС

  Выразите через

  где М - точка отрезка АС и АМ : МС = 1 : 2.

  Ответ:

  

 

  8. В прямоугольном треугольнике АВС угол С = 90°, АС = 12, sin А = 0,8. Найдите ВС, высоту СС₁ и длину отрезка ВС₁.

  Ответ: ВС = 16; СС₁ = 9,6; ВС₁ = 12,8.

 

  9. В треугольнике АВС угол В = 60°, угол А = 50°. Окружность, проходящая через точки В и С вторично пересекает стороны АС и АВ в точках K и L соответственно. Найдите угол ALK.

  Ответ: 70°.

 

  

  12. Точки А, В, С и D в указанной последовательности лежат на окружности радиуса 10 и делят её в отношении 2 : 3 : 4 : 3. Найдите длину отрезка, соединяющего середины сторон АВ и AD.

  Ответ: 2,5(√2 + √6).

 

Дополнительные задания повышенного уровня сложности

для учащихся с высоким уровнем подготовки

 

  13. В треугольнике АВС на стороне АС выбрана такая точка F, что угол ABF : угол FBC = 2 : 3 и отрезок BF разбивает треугольник АВС на два равнобедренных треугольника. Найдите углы треугольника АВС.

  Ответ: угол А = 36°, угол В = 90°, угол С = 54° или угол А = (32 ⁸/₁₁)°, угол В = (81 ⁹/₁₁)°, угол С = (65 ⁵/₁₁)°. Угол А = (77 ¹/₇)°, угол В = (64 ²/₇)°, угол С = (38 ⁴/₇)°.

 

  14. В треугольнике АВС, угол В = 80°, проведена биссектриса BL. Через точку L к окружности, описанной около треугольника BCL, проведена касательная, пересекающая сторону АВ в точке М. Найдите угол ALM.

  Ответ: 40°.

46