Тесты по математике .
1. Среднее арифметическое чисел x; -2,1 и 3,3 равно 0,7. Найдите х.
A) -0,6 *B) 0,9 C) 0,8 D) -0,3
2. Вычислите: 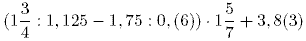
A) 2 1/7 B) 1 1/7 C) 2 2/7 *D) 2
3. В каком ответе знаки cos580°, sin(-550)° и tg(-440)° приведены в порядке их написания? *A) -,+,- B) +,+,- C) +,+,+ D) -,-,-
4. При каких значениях α вектор 2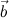 + α
+ α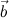 перпендикулярен вектору
перпендикулярен вектору 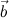 -
- 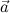 , если
, если 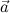 (1;-1; 3) и
(1;-1; 3) и 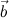 (4; 3; 0)? A) 7/11 B) -6/13 C) 2,1 *D) 5/6
(4; 3; 0)? A) 7/11 B) -6/13 C) 2,1 *D) 5/6
5. В прямоугольнике перпендикуляр, опущенный из вершины на диагональ, делит прямой угол на две части в отношении 3:2. Найдите угол между этим перпендикуляром и другой диагональю. A) 22,5° *B) 18° C) 45° D) 72°
6. Высота равнобедренного треугольника равна 6, а основание больше боковой стороны на 6. Найдите основание этого треугольника. A) 15 *B) 16 C) 18 D) 24
7. Дано несколько натуральных чисел, сумма которых равна 77. Если каждое из этих чисел уменьшить на 4, то сумма новых чисел будет равна 53. Сколько чисел было дано? A) 4 *B) 6 C) 8 D) 12
8. Сколько квадратных сантиметров содержится в 2м2 3дм2 4см2?
A) 21034 *B) 20304 C) 2034 D) 20244
9. При делении натурального числа на 18 в частном получили 14 и в остатке 11. Чему равно делимое? A) 173 B) 243 C) 253 *D) 263
10. Какое из высказываний относительно натуральных чисел ложное?
A) на 5 делятся все числа, которые оканчиваются на цифры 0 или 5
*B) на 4 делятся все числа, которые оканчиваются цифрой 0 или 4
C) чтобы число делилось на 12, достаточно, чтобы оно делилось на 3 и на 4
D) наименьшим кратным данных чисел будет наименьшее число, которое делится без остатка на эти числа
11. Найдите значение выражения: 27*23 – 24*23 + 21*19 - 18*19 + 17*11 – 14*11.
A) 143 *B) 159 C) 165 D) 203
12. Какое из нижеследующих высказываний, сформулированных относительно натуральных чисел, ложно?
A) на 15 делятся все числа, которые делятся на 3 и 5
*B) если число делится на 3, то оно делится на 9
C) наибольшее число, на которое делятся все данные числа без остатка, является наибольшим общим делителем этих чисел
D) если из двух слагаемых одно делится на 11, а второе не делится на 11, то их сумма не делится на 11
13. Как изменится разность, если уменьшаемое уменьшить на 24 и вычитаемое уменьшить на 12?
*A) уменьшится на 12 B) увеличится на 24
C) увеличится на 12 D) уменьшится на 36
14. В туристической группе отношение числа мужчин к числу женщин равно 5:2. Какое из следующих чисел не может быть числом туристов в группе?
A) 21 B) 35 *C) 65 D) 28
15. Найдите число, обратное числу -1,5.
*A) -2/3 B) 2/3 C) 1,5 D) -0,75
16. Вычислите: 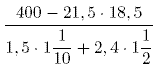
A) 5/7 *B) 3/7 C) 3/5 D) 2/7
17. Упростите выражение: 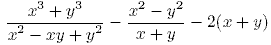
A) 2х B) -2у C) 2y *D) -2х
18. Разложите на множители квадратный трёхчлен: х2 - х - 2.
*A) (х + 1)(х - 2) B) (х - 1)(х + 2) C) (х + 1)(х + 2) D) (х — 1)(х — 2)
19. Упростите выражение: а(b - с) + b(с - а) - с(b - а).A) -2ас B) 2 *C) 0 D) 2аb
20. Найдите значения а и b, если функции f(х) = 2 - ах2 и g(х) = 2b + х принимают одинаковые значения при x = 1 и х = 0.
A) а = 1, b = 1 B) а = 1, b = -1 *C) а = -1, b = 1 D) а = -1, b = -1
21. Найдите область определения функции: 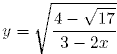
A) (-∞; ∞) *B) (1,5; ∞) C) (-∞; 1,5) D) (0; 3)
22. Сколько процентов числа 4 составляет разность между ним и 3% числа 20?
*A) 85 B) 80 C) 75 D) 90
23. Сумма двух чисел равна 6,5. Одно из них в 4 раза меньше другого. Найдите большее из них. A) 4 B) 5,3 *C) 5,2 D) 6
24. Поезд, длина которого 400 м, проехал тоннель длиной 500 м за 30 с. Найдите скорость поезда. A) 25 м/с *B) 30 м/с C) 40 м/с D) 35 м/с
25. Когда турист проехал 0,35 всего пути, ему осталось проехать до середины пути еще18,3 км. Какова длина всего пути? A) 110 км B) 98 км C) 102 км *D) 122 км
26. На карте расстояние между двумя городами равно 4,5 см. Найдите истинное расстояние (км) между этими городами, если масштаб карты 1:2 000 000
A) 9 км B) 900 км *C) 90 км D) 0,9 км
27. Найдите значение x2 + x2x1 + x1, если x1 и х2 - корни квадратного уравнения 2х2 + 7х - 3 = 0. A) -2 B) -4 C) -3 *D) -5
28. Решите неравенство: (x – 2)/ (x + 3) ≥ 0 A) [-3: 2) *B) (-∞; -3) U [2; ∞) C) (-3; 2] D) (-∞; -3)
29. Решите неравенство: |x|·(x - 1/8)
C) (-∞; 0) U (0; 1/8) D) (0; 1/8)
30. Выполните действия: 1/16 · (0,312 : 0,3 - 1 1/25) + 3/18.
A) -1/16 B) 1/4 *C) 3/18 D) -1/8
31. Разложите на множители: 25 - (2с - 1)2. A) (4 - 2c)(6 + 2c) *B) (4 + 2c)(6 - 2c)
C) (4 - 2c)(6 - 2c) D) (2c -4)(2c - 6)
32. Решите неравенство: (х - 2)(х - 3)
*A) (2; 3) B) (-∞; 2) U (3; ∞) C) (-∞; -2) U (3; ∞) D) (-∞; -3) U (2; ∞)
33. Вычислите: 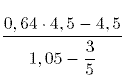 A) 0,36 B) 0,64 C) -0,36 *D) -3,6
A) 0,36 B) 0,64 C) -0,36 *D) -3,6
34. Какому из данных чисел равно число 0,(36)?
*A) 4/11 B) 4/18 C) 1/9 D) 2/3
35. Один из смежных углов на 20° больше другого. Найдите эти углы.
A) 20°; 160° *B) 80°; 100° C) 132°; 152° D) 92°; 112°
36. Найдите смежные углы, которые получаются при пересечении двух прямых, если их градусные меры относятся как 5:7.
A) 42°; 138° *B) 75°; 105° C) 36°; 144° D) 38°; 142°
37. Один из смежных углов на 16° больше другого. Найдите эти смежные углы.
A) 16°, 164° B) 80°, 96° C) 148°, 32° *D) 82°, 98°
38. Угол при основании равнобедренного треугольника равен 70°. Найдите угол, смежный с углом при вершине. A) 100° B) 90° *C) 140° D) 50°
39. Радиус круга 5. Найдите длину дуги кругового сектора, соответствующей центральному углу в 36°. A) 2π *B) π C) π/2 D) π/3
40. Окружность вписана в квадрат с диагональю 2√2 см. Чему равна длина этой окружности? A) 4π *B) 2π C) π√2 D) 8π
41. Площадь одной боковой грани куба равна 16. Чему равен объем куба?
A) 60 B) 62 C) 66 *D) 64
42. Высота равнобедренного треугольника равна 8, а основание больше боковой стороны на 2. Найдите основание этого треугольника.
A) 16 B) 18 C) 15 *D) 12
43. Чему равна диагональ прямоугольного параллелепипеда, линейные размеры которого 3; 4 и 2√14? A) 11 B) 7 C) 10 *D) 9
44. Один из катетов прямоугольного треугольника 4√2 , а гипотенуза относится к другому катету как 5:3. Найдите площадь треугольника.
A) 15 B) 24 C) 20 *D) 12
45. Найдите площадь поверхности куба, диагональ которого равна √3.
A) 9 *B) 6 C) 4,5 D) 3
46. В каком ответе знаки sin880°, cos(-460)° и tg650° приведены в порядке их написания? A) -,-,- B) +,+,- *C) +,-,- D) -,-,+
47. Укажите значение дроби:
2cos2a – sin2a
2sin2a – sin2a если известно, что tgа = -1/2.
A) -4 *B) 2 C) 1/4 D) 4
48. Косинус суммы двух углов треугольника равен -1/3. Найдите косинус третьего угла. A) 2/3 *B) 1/3 C) π/3 D) -2/3
49. Упростите выражение sin2x + cos2x + tg2x.
A) -1/sin2x B) -1/cos2x C) 1/sin2x D) 1/cos2x
50. Упростите:
1 – cos2a
1 + tg2a *A) 1/2 sin22a B) sin22a C) cos22a D) 1/2 cos22a
51. Укажите корень уравнения: 2sin2x - sin2x = 0 из промежутка (0°; 90°].
A) 45° B) 90° C) 30° D) 60°
52. Число 8 составляет 30% числа b. Сколько процентов числа b + 8 составляет число b? A) 1300/17 *B) 1000/13 C) 830/11 D) 1307/17
53. Какое из следующих чисел делится с остатком на 36?
A) 2016 B) 3924 C) 8244 *D) 2648
54. Какие из чисел х = 30112, у = 3,3*105 и z = 102488 делятся на 12 с остатком?
A) только z B) только у C) только х *D) только x и z
55. Сумма двух чисел равна 4,8. Одно из них в 3 раза меньше другого. Найдите меньшее из этих чисел. A) 1,4 *B) 1,2 C) 1,6 D) 2,1
56. Упростите: -6 - 2(2 - у) - 2у + 2. A) -8 - 4у *B) -8 C) 8 - 4у D) 8
57. Вычислите: 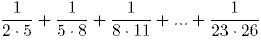
A) 3/20 B) 5/17 C) 15/34 *D) 2/13
58. Какова область определения функции: f(x) = 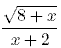 ?
?
A) (—∞; 8] B) (-∞; 8) C) (-∞;-2) U (-2; 8) *D) [—8; —2) U (—2; ∞)
59. Составьте квадратное уравнение, корни которого равны 2+√3 и 2-√3.
A) х2 + 4х + 1 = 0 B) х2 + 4х - 1 = 0 C) х2 - 4х - 1 = 0 *D) х2 - 4х + 1 = 0
60. Найдите наименьшее целое значение k, при котором уравнение х2 - 2(k + 2)х + 11 + k2 = 0 имеет два различных действительных корня. A) 1 B) -2 C) -1 *D) 2
61. Один из корней квадратного уравнения х2 - 13х + q = 0 равен 7. Найдите второй корень. A) 20 B) -42 C) -6 *D) 6
62. Какие из формул верны для геометрической прогрессии?
1) bn = b1qn-1 2) b2n = bn-1 * bn+2 3) Sn = b1(1-qn)/(1-q)
A) 3 *B) 1;3 C) 1 D) 2;3
63. Какую цифру надо поставить вместо точки 2468.13579, чтобы полученное число делилось на 9 нацело? A) 4 *B) 0 C) 7 D) 8
64. Решите уравнение: 2cos4х + √2 = 0. A) 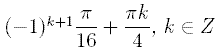
B) 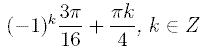 C)
C) 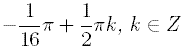 *D)
*D) 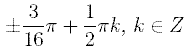
65. Упростите выражение: 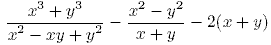
A) 2х B) -2у C) 2y *D) -2х
66. Два предмета в сумме стоят 75100 сум. Если стоимость первого уменьшить на 20%, а второго увеличить на 10%, то вместе они будут стоить 65870 сум. Укажите первоначальную стоимость первого предмета.
A) 19200 сум B) 66960 сум *C) 55800 сум D) 23160 сум
67. Решите неравенство: (х + 2)(х + 3)
*A) (-3; -2) B) (-∞; -3) U (2; ∞) C) (-2; 3) D) (-∞; -2) U (3; ∞)
68. Упростите: (tgx + ctgx)2 - (tgx - ctgx)2. *A) 4 B) -4 C) -2 D) 0
69. Упростите: sin2a + sin2β - sin2a·sin2β + cos2a·cos2β. *A) 1 B) 0 C) -1 D) -2
70. Расставьте в порядке возрастания числа: a = 49/150; b = 102/300; c = 22/75.
A) а b B) b
71. Чему равно значение выражения: 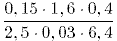 ?
?
A) 2 *B) 0,2 C) 5/8 D) 2/5
72. Упростите выражение: |х — у| — |z — у| — |z — х|, если х
A) 2у-2х *B) 2y-2z C) 2z-2y D) 2х
73. В поезде было 936 пассажиров. Причем мужчин было в 7 раз, а женщин в 5 раз больше, чем детей. Сколько в поезде было женщин?
A) 320 *B) 360 C) 350 D) 375
74. Какому из указанных чисел равна сумма: 1,015*10-5 + 3,14*10-4?
A) 4,155*10-5 *B) 3,2415*10-4 C) 4,155*10-9 D) 1,329*10-4
75. Разложите на множители: 9 - (2с - 1)2
*A) 4(с + 1)(2 - с) B) 2(с - 1)(с + 2) C) 4(с - 1)(с + 1) D) (3с - 1)(с + 4)
76. Выполните действия: 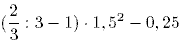
*A) -2 B) -5 C) 1,5 D) -0,2
77. Сумма двух чисел равна 6,5. Одно из них в 4 раза меньше другого. Найдите большее из них. A) 5 B) 6 C) 4 *D) 5,2
78. Среднее арифметическое чисел 5,4; у и -2,2 равно 1,2. Найдите у.
A) 1,2 B) -0,8 C) -0,4 *D) 0,4
79. Истинное расстояние между двумя городами 200 км. Каким будет это расстояние (мм) на карте с масштабом 1:5000000?
A) 10 мм B) 100 мм C) 20 мм *D) 40 мм
80. Какой цифрой заканчивается разность: 3*5*9*17* ... *1023 - 7?
*A) 8 B) 3 C) 0 D) 9
81. Некоторое число а при делении на 3 дает остаток 1, а при делении на 4 - остаток 3. Найдите остаток от деления числа а на 6. A) 3 B) 7 C) 5 *D) 1
82. Угол при основании равнобедренного треугольника равен 70°. Найдите угол, смежный с углом при вершине. A) 100° B) 90° *C) 140° D) 50°
83. Вычислите: 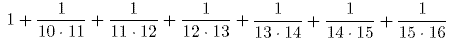
*A) 1 3/80 B) 1 3/40 C) 1,16 D) 1 7/80
84. При делении 215 на 16 получили остаток, равный 7. Чему равно частное?
A) 12 *B) 13 C) 9 D) 11
85. Деталь в масштабе 1:5 имеет длину 2,1 см. Какую длину (см) имеет данная деталь в масштабе 1:3,5? *A) 3 B) 3,1 C) 3/5 D) 2 1/3
86. В каком пункте приведен переместительный закон сложения?
*A) a + b = b + a B) (a + b) + c = a + (b + c) C) (a + b) c = a c + b c
D) (a + b) - c = a + (b - c)
87. В каком пункте приведен сочетательный закон сложения?
A) a + b = b + a *B) (a + b) + c = a + (b + c) C) (a + b) c = a c + b c
D) (a + b) - c = a + (b - c)
88. В каком пункте приведен распределительный закон умножения относительно сложения? A) a + b = b + a B) (a + b) + c = a + (b + c)
*C) (a + b) c = a c + b c D) (a + b) - c = a + (b - c)
89. В каком пункте приведен переместительный закон умножения?
*A) a . b = b . a B) (a . b) . c = a . (b . c) C) (a + b) c = a c + b c
D) (a + b) + c = a + (b + c)
90. В каком пункте приведен сочетательный закон умножения?
A) a . b = b . a *B) (a . b) . c = a . (b . c) C) (a + b) c = a c + b c
D) (a + b) + c = a + (b + c)
89. В каком пункте приведена формула нахождения p процента от числа a?
*A) b = � � 100 B) p = �
� 100 B) p = � � 100 C) a = �
� 100 C) a = �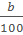 � p D) a = b 100
� p D) a = b 100
90. В каком пункте приведена формула нахождения числа по его p проценту b?
A) b = � � 100 B) p = �
� 100 B) p = � � 100 *C) a = �
� 100 *C) a = �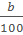 � p D) a = b 100
� p D) a = b 100
91. В каком пункте приведена формула нахождения процентного отношения двух чисел a и b? A) b = � � 100 *B) p = �
� 100 *B) p = � � 100 C) a = �
� 100 C) a = �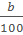 � p D) a = b 100
� p D) a = b 100
92. При выполнение какого условия квадратное уравнение ax2 + bx + c = 0 имеет два действительных корней? *A) b2 - 4 a c 0 B) b2 - 4 a c 0
C) b2 - 4 a c = 0 D) b2 - 4 a c = 1
93. При выполнение какого условия квадратное уравнение ax2 + bx + c = 0 имеет только один действительный корень? A) b2 - 4 a c 0 B) b2 - 4 a c 0
*C) b2 - 4 a c = 0 D) b2 - 4 a c = 1
94. При выполнение какого условия квадратное уравнение ax2 + bx + c = 0 не имеет действительных корней? A) b2 - 4 a c 0 *B) b2 - 4 a c 0
C) b2 - 4 a c = 0 D) b2 - 4 a c = 1
95. Найдите неверное утверждение? A) Если a b, то b a
B) Если a b и b c, то a c *C) Если a b и b c, то a c
D) Если a b, то a + c b + c
96. Найдите неверное утверждение? A) Если a b и c 0, то ac bc
B) Если a b и b c, то a c *C) Если a b и c 0, то ac bc
D) Если a b, то a + c b + c
97. Найдите неверное утверждение? A) Если a b и c d, то a + c b + d
B) Если a b и b c, то a c C) Если a b и c 0, то ac bc
*D) Если a b и c d, то a + c b + d
98. В каком пункте приведена формула n- го члена арифметической прогрессии?
A) bn+1 = bn q b1≠ 0, q≠ 0 B) an+1 = an+d
C) bn = b1 qn-1 *D) an = a1 + d (n - 1)
99. В каком пункте приведена формула n- го члена геометрической прогрессии?
A) bn+1 = bn q b1≠ 0, q≠ 0 B) an+1 = an+d
*C) bn = b1 qn-1 D) an = a1 + d (n - 1)
100. В каком пункте приведена формула определения геометрической прогрессии?
*A) bn+1 = bn q b1≠ 0, q≠ 0 B) an+1 = an+d
C) bn = b1 qn-1 D) an = a1 + d (n - 1)






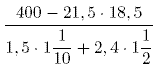
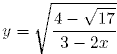
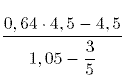 A) 0,36 B) 0,64 C) -0,36 *D) -3,6
A) 0,36 B) 0,64 C) -0,36 *D) -3,6



















