Текстовые задачи на смеси

Текстовые задачи на смеси

Презентация для подготовки к ЕГЭ и ОГЭ

Составитель учитель физики и математики МКОУ СОШ с. Гастелло Сарварова В.Б.

Опробирована на МРО учителей математики.

2016г

К 30%-ному раствору серной кислоты добавили 60 г воды и получили 10%-ный раствор. Найдите массу первоначального раствора серной кислоты.

• Пусть х г - масса первоначального раствора серной кислоты.
• 0,3х=0,1(х+60)
• 0,3х=0,1х+6
• 0,2х=6
• 0,1х=3
• Х=30
• 30г- масса первоначального раствора серной кислоты .

Какое количество воды надо добавить к 3л 36%-ного раствора соли, чтобы получить 24%- ный раствор?

• Пусть х л –необходимое количество воды.
• 3·0,36=0,24(х+3)І·100
• 108=24(х+3)
• 108=24х+72
• 24х=36
• Х=1,5
• 1,5л воды –необходимое количество воды

Один сплав содержит 55% цинка, а другой- 70% цинка. После переплавки получили 750г нового сплава с 60%-ным содержанием цинка. Сколько граммов цинка содержалось в первом сплаве?

2

• Пусть масса первого сплава х г, тогда масса второго сплава (750-х)г.
• В первом сплаве 0,55х г цинка, во втором 0,7(750-х)г цинка. В новом сплаве 0,6·750г цинка.
• 0,55х+0,7(750-х)=0,6·750
• 0,55х+0,7·750-0,7·х=0,6·750
• -0,15х=750(0,6-0,7)
• 0,15х= 750·(-0,1)
• х=500
• 500г- масса первого сплава;
• 0,55·500=275г- масса цинка в первом сплаве

1

3

Смешали два раствора соляной кислоты 15%-ной и 7%-ной концентрации, после чего получили 480г раствора 10%-ной концентрации. Найдите массу 7%-ного раствора .

• Пусть масса первого раствора х г, тогда масса второго раствора (480-х)г.
• В первом растворе 0,15х г кислоты, во втором 0,07(480-х)г кислоты. В новом растворе 0,1·480г кислоты.
• 0,15х+0,07(480-х)=0,1·480
• 0,15х+0,07·480-0,07·х=0,1·480
• 0,08х=480(0,1-0,07)
• 0,08х= 480·0,03
• Х=180
• 180г- масса первого сплава; 300г- масса второго сплава

Сколько граммов воды надо добавить к 180г сиропа содержащего 25% сахара. Чтобы получить сироп, концентрация которого равна 20%

• Пусть х г –необходимое количество воды.
• 0,25·180=0,20(х+180 ) І·100
• 25·180=20(х+180)
• 180(25-20)=20х
• 180·5=20х
• Х=45
• 45г- необходимое количество воды

Сколько граммов сахарного сиропа, концентрация которого 25%, надо добавить к 200г воды, чтобы в полученном растворе содержание сахара составляло 5%?

• Пусть х –необходимое количество сиропа.
• 0,25х=0,05(х+200 ) І·100
• 25·х=5(х+200)
• х(25-5)=1000
• Х=1000:20
• Х=50
• 50г – необходимое количество сиропа

Сколько граммов 75%-ного раствора кислоты надо добавить к 30 г 15%-ного раствора кислоты, чтобы получить 50%-ный раствор кислоты?

• Пусть х –необходимое количество 75%-ного раствора кислоты.
• 0,75х+0,15·30= 0,5(х+30 ) І·100
• 75х+15·30= 50(х+30)
• х(75-50)=30(50-15)
• 25х=30·35
• 25х=1050
• х=42
• 42г - необходимое количество 75%-ного раствора кислоты.

Сколько граммов 15%-ного раствора соли надо добавить к 50 г 60%-ного раствора соли, чтобы получить 40%-ный раствор соли?

• Пусть х –необходимое количество 15%-ного раствора соли.
• 0,15х+0,60·50= 0,40(х+50 ) І·100
• 15х+60·50= 40(х+50)
• х(40-15)=50(60-40)
• 25х=50·20
• 25х=1000
• Х=40

40г - необходимое количество 15%-ного раствора соли

К 40% -ному раствору соляной кислоты добавили 50г чистой кислоты, после чего концентрация раствора стала равной 60%. Найдите первоначальную массу раствора.

• Пусть х г –первоначальная масса раствора кислоты.
• 0,40х+1,00·50 = 0,60(х+50)
• Кислота
• 40х+100·50= 60(х+50)
• 20х=2000
• Х=100
• 100г- первоначальная масса раствора

Какое количество воды нужно добавить в 1 литр 9%-ного раствора уксуса, чтобы получить 3%-ный раствор

• Пусть х л –необходимый объём воды .

Содержание уксуса в 1л раствора

Содержание уксуса в (1+х)л

1·0,09

0,03(1+х)

1·0,09=0,03(1+х)

9=3(1+х)

3х=9-3

3х=6

Х=2

2л- необходимый объём воды.

В43 №13

Первый сплав содержит 5% меди, второй -14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

2015

• Пусть масса первого сплава х кг, тогда масса второго сплава (7+х)кг.
• В первом сплаве 0,05х кг меди, во втором 0,14(7+х)кг меди. В новом сплаве 0,10·(2х+7) меди.
• 0,05х+0,14(7+х)=0,10·(2х+7)
• 5х+14(7+х)=10·(2х+7)
• 19х+98=20х+70
• х= 28
• 28кг- масса первого сплава;
• 2х+7= 63(кг) масса третьего сплава

Смешав 70%-й и 60%-й раствор кислоты и добавив 2кг чистой воды, получили 50%-й раствор кислоты. Если бы вместо 2кг воды добавили 2кг 90%-го раствора той же кислоты, то получили бы 70% -й раствор кислоты. Сколько килограммов 70%-го раствора использовали для получения смеси?

В6№13

2015

• Пусть масса первого раствора х кг, тогда масса второго раствора у кг.
• В первом растворе 0,70х кг кислоты, во втором 0,60 у кг кислоты. В новом растворе 0,50(х+у+2) кг кислоты.
• 0,70х+ 0,60у= 0,50(х+у+2)
• Во втором случае : 0,70х+0,60у+0,9·2= 0,7(х+у+2)

• 3кг- масса 70%-го раствора кислоты

В7№13

В сосуд, содержащий 10л 24%-го водного раствора некоторого вещества, добавили 5л воды. Сколько процентов составит концентрация получившегося раствора?

2015

Пусть х%- концентрация раствора конечного раствора, объём которого 15л. Содержание некоторого вещества в 10л равно 0,24·10л.

0,24·10= 15х

2,4=15х

Х= 2,4:15

Х=0,16

16% - концентрация конечного раствора .

В8№13

Первый сплав содержит 5% меди, второй 11% меди. Масса второго сплава больше первого на 4 кг. Из двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

2015

• Пусть масса первого сплава х кг, тогда масса второго сплава (4+х)кг.
• В первом сплаве 0,05х кг меди, во втором 0,11(4+х)кг меди. В новом сплаве 0,10·(2х+4) меди.
• 0,05х+0,11(4+х)=0,10·(2х+4)

5х+11(4+х)=10·(2х+4)

• 16х+44=20х+40
• 4х= 4
• х=1
• 1кг- масса первого сплава;
• 2+4= 6(кг) масса меди в третьем сплаве

Если слить 8кг и 2кг растворов серной кислоты разной концентрации. То получится 12%-й раствор кислоты. При смешивании двух одинаковых масс тех же растворов получим 15%-й раствор. Определите первоначальную концентрацию каждого раствора.

• Пусть х- концентрация первого раствора, у- концентрация второго раствора. Содержание кислоты в первом растворе -8х кг, во втором 2у кг. Содержание в смеси-0,12·10 кг.
• Второй случай: содержание кислоты в первом растворе 2х кг и во втором 2у кг, а в новой
• При вычитании из первого уравнения второго получим: 6х=0,6
• 10%-концентрация первого раствора кислоты; 20% -концентрация второго раствора кислоты.

Имеются два сплава, содержащие вещества А и В. Первый сплав содержит 20% вещества А. а второй -30% вещества В. Взяли некоторое количество первого сплава и вдвое меньшее количества второго сплава сплавили их с 1 кг чистого вещества А. В результате содержание вещества А в новом сплаве стало больше процентного содержания вещества В во втором сплаве на 10%. Определите массу нового сплава .

Пусть х кг масса первого сплава, тогда масса вещества А в этом сплаве равна 0,2х кг вещества А. Масса вещества В во втором сплаве 0,7 кг. Масса нового сплава (х++ 1) кг.

0,2х+0,7(0,5х) +1= (0,1+0,3) +1)

0,2х+0,35х+1= 0,4 (х+1) ;

0,55х+1=0,6х+0,4;

0,05х=0,6

х=12; 12кг- масса первого сплава;

+1)= 12+6+1=19(кг)-масса нового сплава.

Ответ : 19кг.

Имеются два сосуда, содержащие 4 кг и 6 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 35% кислоты. Если же слить равные массы этих растворов, то получим раствор, содержащий 36% кислоты. Сколько килограммов кислоты содержится в каждом растворе?

Пусть в первом растворе содержится х% кислоты или 4х кг, а во втором –у% кислоты или 6у кг.

Тогда после их сливания получится новая смесь, содержащая : 4х+6у= 0,35·10 (кг) 35% кислоты.

После сливания равных масс кислоты получится смесь, содержащая 36% кислоты:

4х+4у=0,36·8.

После решения системы: у=0,31; х=0,41.

4х=4·0,41=1,64(кг)-масса кислоты в первом растворе; 6·0,31=1,86(кг)- масса кислоты во втором растворе.

Имеются два раствора серной кислоты в воде, первый 40%-й, второй- 60%-й. Эти растворы смешали, после чего добавили воды и получили 20% -й раствор кислоты. Если бы вместо 5 кг воды добавили 5кг 80% -го раствора, то получили бы 70%-й раствор. Определите количество 40%-го и 60% -го раствора.

х кг –масса первого раствора, у кг- масса второго раствора. 0,4кг масса кислоты в первом растворе, 0,6у кг- масса кислоты во втором растворе. (х+у+5) – масса нового раствора.

Масса 40% -го раствора 1кг; 60%-го – раствора-2кг .

задача

Тренировочная работа 53

В сосуд , содержащий 5л 12%-го водного раствора некоторого вещества, добавили 7л воды. Сколько процентов составляет концентрация получившегося раствора?

53.1

Пусть х%-концентрация нового раствора; 0,12·5 л –объем кислоты в первоначальном объёме.

(5+7)л- объём нового раствора; х(12)л содержание кислоты в новом растворе.

0,12·5=12х

0,6=12х

Х= 0,6: 12

Х=0,05

5% - концентрация нового раство ра

Смешали некоторое количество 15%-го раствора некоторого вещества с таким же количеством 19%-го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

53.2

Пусть х кг- масса 15%-го и 19%-го растворов. Концентрация нового раствора –n%, а 2х кг- масса нового раствора. 2х·n кг- содержание вещества в новом растворе.

0,15х+0,19х=2х n

0,15+0,19= 2n

0,17=n

17 %-концентрация нового раствора.

53.3

Смешали 4л 15%-го водного раствора некоторого вещества с 6л 25%-го водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

0,15·4+0,25·6=10 n

0,6+1,5= 10n

2,1=10n

0,21= n

21 %-концентрация нового раствора.

Имеется два сплава . Первый сплав содержит 10% никеля, второй -30% никеля. Из двух этих сплавов получили третий сплав массой 200кг, содержащий 5% никеля. На сколько килограммов масса первого сплава меньше массы второго?

53.5

Пусть х кг- масса первого сплава, тогда масса второго (200-х)кг.

0,1х кг- содержание никеля в первом сплаве; 0,3(200-х) кг- кг- содержание никеля во втором сплаве. Содержание никеля в третьем сплаве -0,05·200 кг.

0,1х+0,3(200-х)=0,05·200

0,1х-0,3х+60=50

0,2х=10

Х=50

50 кг- масса первого сплава; 150 кг- масса второго сплава.

150-50=100(кг)-н а столько килограммов масса первого сплава меньше массы второго

Тренировочная работа 54

Первый сплав содержит 10% меди, второй 40% меди. Масса второго сплава больше первого на 3 кг. Из двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

54,1

Пусть масса первого сплава х кг, тогда масса второго сплава (3+х)кг.

В первом сплаве 0,1х кг меди, во втором 0,4(3+х)кг меди. В новом сплаве 0,3·(2х+3) меди.

0,1х+0,4(3+х)=0,3·(2х+3)

х+4(3+х)=3·(2х+3)

5х+12=6х+9

х= 3

3кг- масса первого сплава;

2х+3= 9(кг) масса третьего сплава

Имеются три одинаковых по массе сплава. Известно, что меди во втором сплаве на 10% больше, чем в первом сплаве, а в третьем сплаве на 10% больше, чем во втором. Из этих трёх сплавов получили четвёртый сплав, содержащий 19% меди. Сколько процентов меди содержит первый сплав?

54.2

Концентрация вещества, %

Масса вещества,

Х

кг

m

Х+0,1

Содержание вещества, кг

Масса четвертого, кг

m

Хm

Х+0,2

Содержание вещества,кгх

(x+0,1)m

m

3m

(x+0,2)m

0,19(3m)

Xm+(х+0,1)m+(x+0,2)m=0,19(3m)

3x=0,27

X=0,09; 9% меди содержит первый сплав .

Смешав 30%-й и 60%-й раствор кислоты и добавив 10кг чистой воды, получили 36%-й раствор кислоты. Если бы вместо 10кг воды добавили 10кг 50%-го раствора той же кислоты, то получили бы 41% -й раствор кислоты. Сколько килограммов 30%-го раствора использовали для получения смеси?

54.3

Пусть масса первого раствора х кг, тогда масса второго раствора у кг.

В первом растворе 0,30х кг кислоты, во втором 0,60 у кг кислоты. В новом растворе 0,50(х+у+10) кг кислоты.

0,30х+ 0,60у= 0,36(х+у+10)

Во втором случае : 0,30х+0,60у+0,50·10= 0,41(х+у+10)

60кг- масса 30%-го раствора кислоты

Имеются два сосуда. Первый содержит 30кг, а второй -20кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор содержащий 68% кислоты. Если смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

54.4

Пусть х%- концентрация первого раствора, у%- концентрация второго раствора. Содержание кислоты в первом растворе -30х кг, во втором 20у кг. Содержание в смеси-0,68·50 кг.

Второй случай: содержание кислоты в первом растворе 20х кг и во втором 20у кг, а в новой

Х=0,6; 6 0%-концентрация первого раствора кислоты; 0,6·30=18 (кг)- масса кислоты в первом сосуде.

Практикум и диагностика

В сосуд , содержащий 8л 15%-го водного раствора некоторого вещества, добавили 4л воды. Сколько процентов составляет концентрация получившегося раствора?

53.1

Пусть х%-концентрация нового раствора; 0,15·8 л –объем кислоты в первоначальном объёме.

(8+4)л- объём нового раствора; х(12)л содержание кислоты в новом растворе.

0,15·8=12х

1,2=12х

Х= 1,2: 12

Х=0,1

10% - концентрация нового раство ра

Смешали некоторое количество 13%-го раствора некоторого вещества с таким же количеством 23%-го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

53.2

Пусть х кг- масса 13%-го и 23%-го растворов. Концентрация нового раствора –n%, а 2х кг- масса нового раствора. 2х·n кг- содержание вещества в новом растворе.

0,13х+0,23х=2х n

0,15+0,19= 2n

0,36=6n

n=0,18

18 %-концентрация нового раствора.

53.3

Смешали 7л 20%-го водного раствора некоторого вещества с 3л 10%-го водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

0,2·7+0,10·3=10 n

1,4+0,3= 10n

1,7=10n

0,17= n

17 %-концентрация нового раствора.

Имеется два сплава . Первый сплав содержит 20% никеля, второй -5% никеля. Из двух этих сплавов получили третий сплав массой 100кг, содержащий 11% никеля. На сколько килограммов масса первого сплава меньше массы второго?

53.5

Пусть х кг- масса первого сплава, тогда масса второго (100-х)кг.

0,2х кг- содержание никеля в первом сплаве; 0,05(100-х) кг- кг- содержание никеля во втором сплаве. Содержание никеля в третьем сплаве -0,05·100 кг.

0,2х+0,05(100-х)=0,11·100

0,2х-0,05х+5=11

0,15х=6

Х=40

40 кг- масса первого сплава; 60 кг- масса второго сплава.

60-40=20(кг)-н а столько килограммов масса первого сплава меньше массы второго

Первый сплав содержит 20% меди, второй 30% меди. Масса второго сплава меньше первого на 5 кг. Из двух сплавов получили третий сплав, содержащий 24% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

54,1

Пусть масса первого сплава (х+5) кг, тогда масса второго сплава х кг.

Во первом сплаве 0,2(х+5) кг меди, в первом 0,3х кг меди. В новом сплаве 0,24·(2х+5) меди.

0,2(5+х)+0,3х=0,24 ·(2х+5)

1+0,2х+0,3х=0,48х+1,2)

х=10

10кг- масса первого сплава;

2х+5= 25(кг) масса третьего сплава

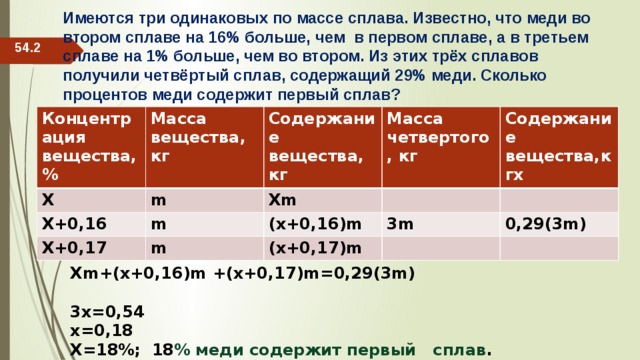
Имеются три одинаковых по массе сплава. Известно, что меди во втором сплаве на 16% больше, чем в первом сплаве, а в третьем сплаве на 1% больше, чем во втором. Из этих трёх сплавов получили четвёртый сплав, содержащий 29% меди. Сколько процентов меди содержит первый сплав?

54.2

Концентрация вещества, %

Масса вещества,

Х

кг

m

Содержание вещества, кг

Х+0,16

m

Масса четвертого, кг

Хm

Х+0,17

Содержание вещества,кгх

(x+0,16)m

m

3m

(x+0,17)m

0,29(3m)

Xm+(x+0,16)m +(x+0,17)m=0,29(3m)

3х=0,54

x=0,18

X=18%; 18 % меди содержит первый сплав .

Смешав 40%-й и 70%-й раствор кислоты и добавив 20кг чистой воды, получили 41%-й раствор кислоты. Если бы вместо 20кг воды добавили 20кг 60%-го раствора той же кислоты, то получили бы 53% -й раствор кислоты. Сколько килограммов 40%-го раствора использовали для получения смеси?

54.3

Пусть масса первого раствора х кг, тогда масса второго раствора у кг.

В первом растворе 0,40х кг кислоты, во втором 0,70 у кг кислоты. В новом растворе 0,41(х+у+20) кг кислоты.

0,40х+ 0,70у= 0,41(х+у+20)

Во втором случае : 0,4х+0,70у+0,60·20= 0,53(х+у+20)

50кг- масса 40%-го раствора кислоты.

Имеются два сосуда. Первый содержит 5кг, а второй -10кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор содержащий 40% кислоты. Если смешать равные массы этих растворов, то получится раствор, содержащий 35% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

54.4

Пусть х%- концентрация первого раствора, у%- концентрация второго раствора. Содержание кислоты в первом растворе -5х кг, во втором 10у кг. Содержание в смеси-0,40·15 кг.

Второй случай: содержание кислоты в первом растворе 5х кг и во втором 5у кг, а в новой

Х=0,2; 2 0%-концентрация первого раствора кислоты; 0,2·5=1 (кг)- масса кислоты в первом сосуде.

Имеется сплав массой 221 кг, состоящий из никеля, меди и марганца. Масса никеля составляет 30% массы меди и марганца, а масса меди составляет 70% массы никеля и марганца. Сколько килограммов марганца содержится в сплаве?

54,5

Масса никеля, кг

Масса никеля, кг

Масса меди, кг

Масса меди, кг

Масса марганца, кг

Масса марганца, кг

С

С

;

a=0,21a+0,21c+0,3c

0,79a=0,51c; a=;

+ c )= 0,7( )=

++C=221; 221C=221·79; C=79; 79КГ МАРГАНЦА СОДЕРЖИТСЯ В СПЛАВЕ.

СПАСИБО ЗА ВНИМАНИЕ

УЧИТЕЛЬ: Сарварова В.Б.