Тема:ДЕЛЕНИЕ ОТРЕЗКА НА 2, 4, 8 РАВНЫХ ЧАСТЕЙ С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ

Тип урока: открытие новых знаний и способов действий

Педагогические задачи: способствовать формированию умений измерять длину отрезка и строить отрезки заданной длины; совершенствовать умения решать арифметические задачи

Планируемые результаты

Предметные:

научатся выполнять решение практических задач, связанных с делением отрезка на равные части, с использованием циркуля и линейки

Метапредметные:

Познавательные: осуществляют моделирование; умеют осознанно и произвольно строить речевое высказывание в устной и письменной форме; осуществляют выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.

Регулятивные: принимают и сохраняют учебную задачу; планируют свои действия в соответствии с поставленной задачей и условиями ее реализации.

Коммуникативные: излагают своё мнение и аргументируют свою точку зрения

Личностные: осознают необходимость самосовершенствования

Этап урока

Содержание деятельности учителя

Содержание деятельности обучающегося

(осуществляемые действия)

Формируемые

способы

деятельности

обучающегося

II. Актуализация опорных знаний.

Устный счет.

Интеллектуальная разминка

Организует устный счет с целью актуализации знаний.

Отвечают на вопросы учителя по материалу прошлого урока. Выполняют задания устного счета.

Осуществлять актуализацию личного жизненного опыта. Уметь слушать в соответствии с целевой установкой.

Принимать и сохранять учебную цель и задачу.

Дополнять, уточнять высказанные мнения

– Выполните сравнение величин, поставьте знаки: ,

18 кг 25 г … 18250 г 4 ч 5 мин … 240 мин

18 т 25 кг ... 18025 кг 4 ч 50 мин ... 450 мин

18 ц 25 кг ... 1825 кг 4 ч 3 мин ... 240 мин

18 ц 25 кг ... 18250 кг 4 мин 3 с ... 270 с

18 ц 250г ... 1825 г 4 мин 30 с ... 270 с

Решение:

18 кг 25 г 240 мин

18 т 25 кг = 18025 кг 4 ч 50 мин

18 ц 25 кг = 1825 кг 4 ч 3 мин 240 мин

18 ц 25 кг

18 ц 250 г 1825 г 4 мин 30 с = 270 с

– Из следующих математических записей выберите уравнения:

а) х · 7 = 63 г) а + 15 = 40

б) у + 3 · 8 д) у – 20 60

в) 25 · (653 – 299) е) 15 + 16 · 2

– Устно вычислите корни данных уравнений.

Решение:

III. Открытие нового знания, способа действия.

Работа по учебнику (с. 97).

Задание 1.

Организует работу по открытию нового знания, обеспечивает контроль за выполнением задания.

– Как выполнил задание каждый из учеников?

– Кто выполнил задание правильно? Проверьте, используя циркуль.

– Какую ошибку допустила Катя?  Какую ошибку допустил Саша?

Выполняют задания, отвечают на вопросы, высказывают свое мнение.

– Маша выполнила задание правильно.

– Катя допустила ошибку: радиусы окружностей должны быть больше половины отрезка. Саша допустил ошибку: радиусы окружностей должны быть равны.

Планировать решение учебной задачи: выстраивать алгоритм действий, выбирать действия в соответствии с поставленной задачей. Применять правила делового сотрудничества.

Осуществлять контроль по результату

Задание 2

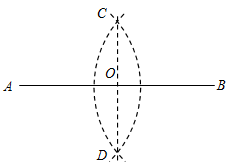
Алгоритм деления отрезка на 2 равные части:

– Из концов отрезка А и В при помощи циркуля проведите две дуги окружности радиуса R. Радиус окружности сделайте несколько большим половины отрезка АВ. Доведите дуги до взаимного пересечения. Таким образом вы получите точки C и D, равноудаленные от отрезка АВ. Проведите через точки С и D прямую линию, пересекающую отрезок АВ. Точка пересечения этой линии и отрезка будет искомой точкой О, в которой отрезок АВ разделяется на две равные части

IV. Включение нового в актив-ное использование в сочетании с ранее изученным, освоенным.

Организует беседу, помогает сделать вывод. Уточняет и расширяет знания обучающихся по теме урока.

Отвечают на вопросы учителя, высказывают свои мнения и предположения. Уточняют и расширяют свои знания по теме урока. Доказывают, аргументируют свою точку зрения.

Выбирать действия в соответствии с поставленной задачей, оценивать уровень владения тем или иным учебным действием, вносить необходимые корректировки в действие после завершения на основе оценки и учёта характера сделанных ошибок. Преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной целью.

Развивать чувство доброжелательности, эмоционально-нравственную отзывчивость. Приводить убедительные доказательства в диалоге, проявлять активность во взаимодействии. Воспроизводить по памяти информацию, необходимую для решения учебной задачи, обосновывать выбор.

Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий

Работа по учебнику (с. 98–100).

Задание 6.

– Не выполняя указанных вычислений, определите, больше или меньше числа 100 результаты действий.

Решение:

2475 – 876 больше 1000 903 · 20 больше 1000

603 + 495 больше 1000 427 : 70 меньше 1000

Задание 7.

– Ответьте на вопросы.

– Во сколько раз 1 кг больше 100 г?

– Во сколько раз 1 ц меньше 1 т?

– Во сколько раз 1 ц больше 10 кг?

Ответы:

– В 10 раз 1 кг больше 100 г.

1 кг = 1000 г, 1000 г : 100 г = 10 (раз).

– В 10 раз 1 ц меньше 1 т.

1 т = 10 ц; 10 ц : 1 ц = 10 (раз).

– В 10 раз 1 ц больше 10 кг.

1 ц = 100 кг; 100 кг : 10 кг = 10 (раз).

Задание 8.

– Какое свойство умножения выражает каждое равенство?

– Сформулируйте каждое свойство.

Объясняют каждое равенство:

1) 324 · 17 = 17 · 324.

џ От перестановки множителей значение произведения не изменяется.

2) (12 · 8) · 30 = 12 · (8 · 30).

џ Сочетательный закон умножения относительно сложения.

3) (165 + 38) · 70 = 165 · 70 + 38 · 70.

Чтобы умножить сумму на число, надо каждое слагаемое умножить на это число, полученные результаты сложить. Это распределительное свойство умножения относительно сложения.

Задание 9.

– Составьте задачу и решите её двумя способами.

Запись: Всего – 3600 пар

Детская обувь – ? пар, три четверти

Женская – ? пар

Решение: I способ

1) 3600 : 4 · 3 = 27000 (пар) – детской обуви.

2) 3600 – 2700 = 900 (пар) – женской обуви.

II способ

1) Какую часть составляет женская обувь? (Одну четвертую часть.)

2) 3600 : 4 · 1 = 900 (пар) – женской обуви.

Задание 10.

– Сколько рублей стоит книга?

Решение:

36 + 36 : 3 · 2 = 36 + 24 = 60 (р.) – стоит книга.

Задание 11.

– Ответьте на вопросы, используя данные таблицы.

– На сколько граммов литр нефти тяжелее литра керосина?

– Чему равна масса 2 л ртути?

– На 40 граммов литр нефти легче литра керосина.

840 – 800 = 40 (г).

– 27 кг 200 граммов весят 2 л ртути.

13 кг 600 г · 2 = 27 кг 200 г.

– Что легче: 2 л бензина или 1 л ртути?

– Во сколько раз масса 80 л морской воды больше массы 1 л керосина?

– Легче 1 л ртути.

690 г · 2 = 1380 г = 13 кг 800 г;

13 кг 800 г 13 кг 600 г.

– В 125 раз масса 80 л морской воды больше массы 1 л керосина.

1 кг 250 г · 80 = 100000 г, 100000 г : 800 г = 125

(раз).

Задание 12

– Составьте выражения и найдите их значения

Решение:

1) 3407 + 19007856 = 19011263

2) 1010203 – 998877 = 11326

3) 196 · 408 = 79968

4) 123140 : 524 = 235

V. Итог урока. Рефлексия

Оценка результатов выполнения заданий на уроке. Организация подведения итогов урока обучающимися.

Проводит беседу по вопросам:

– Что нового узнали на уроке?

– Как разделить отрезок на 2 равные части?

– Какое задание понравилось больше всего?

– Что вызвало затруднение?

– Понравилась ли вам работа на уроке? Оцените себя

Отвечают на вопросы. Определяют свое эмоциональное состояние на уроке. Проводят самооценку, рефлексию

Способность

к самооценке на основе критерия успешности учебной деятельности