Тема уроку: Ознаки зростання і спадання функції.
Цілі уроку:
- ввести ознаку зростання, спадання функції і показати їх застосування при рішенні завдань;
- розвівати пізнавальну активність, інтерес до предмета;
- виховати точність, логічність у мисленні.
Домашнє завдання до уроку: повторити визначення зростаючій і спадаючій функцій.
Хід уроку
1. Організаційний момент.
2. Математична розминка.
На екрані завдання. Учні виконують завдання усно. Відповіді перевіряються за допомогою таблиці «відповідь - буква», яка у кожного на парті, обрані відповіді записують до бланку , з яких виходять прізвища вчених.
Завдання: знайдіть y ' або значення y ' в точці x0 ( Слайд№1,2).


Бланк відповідей ____________________________________
Варіант I
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| відповідь |
|
|
|
|
|
|
|
| буква |
|
|
|
|
|
|
|
Бланк відповідей ____________________________________
Варіант II
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| відповідь |
|
|
|
|
|
|
|
| буква |
|
|
|
|
|
|
|
3. Історична довідка (Слайд№3,4).


Коротка розповідь двох учнів про життя цих учених та їх внесок у вивчення математичного аналізу (учні самі знаходять інформацію, працюючи з додатковою літературою та іншими інформаційними ресурсами). Висновок: вони одночасно розробили основи математичного аналізу; якщо Ньютон виходив із завдань механіки, то Лейбніц - з геометричних задач.
4. Індивідуальні завдання.
Під час математичної розминки ,два учня працюють з індивідуальними завданнями у дошки.
1 завдання.
Вирішити нерівність методом інтервалів: х2 - 4х 0.
2(а, б,в, г) завдання. Вказати проміжки зростання, спадання функцій:
а)у = 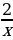 ; б)у = х2 - 6;в) у = - х2 + 4х +6; г)у = 0,2х5 -
; б)у = х2 - 6;в) у = - х2 + 4х +6; г)у = 0,2х5 - 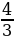 х3
х3
Виконавши завдання а -в, отримуємо проблему: як знайти проміжки монотонності для четвертої функції?
Отже, сформулюйте тему і мету нашого уроку. (Учні самі проговорюють тему ).
5. Введення нового матеріалу (в ході фронтальної бесіди з елементами дослідження).
Яка функція називається зростаючою, спадною? (слайди№5,6,7)


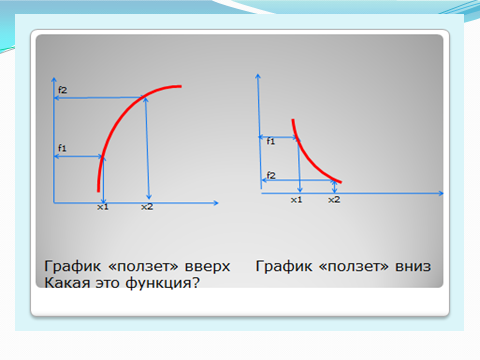
Для функцій, графіки яких зображені на малюнках, вкажіть проміжки зростання, убування (на малюнках графіки різних функцій) (Слайд№8)
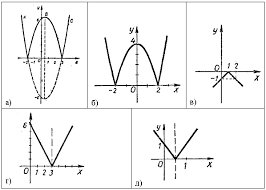
Розбір другого індивідуального завдання.
Як визначити проміжки зростання, спадання функції у = 0,2х5 - 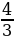 х3.
х3.
Для цього досліджуємо графік деякої функції y = f(x) ,запропонований на рисунку (Слад№9,10)
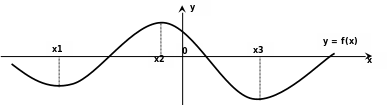























α2
α1
β2
β1
y = f(х)
х1
х2
х
у
0
x3
На кожному зі проміжків (-∞;х
1), (х
1;х
2), (х
2;х
3), (х
3;+∞) побудемо дотичні
Завдання. Проаналізувати розташування дотичних стосовно осі абсцис (кут нахилу) і визначити знаки значень похідної.
Учні самостійно роблять висновок.
Висновок:
1. Достатній ознака зростання функції. Якщо f '(x) 0 в кожній точці інтервалу У, то функція f(х) зростає на У.
2. Достатній ознака спадання функції. Якщо f '(x) 0 в кожній точці інтервалу У, то функція f(х) спадає на У.
Учні разом з учителем складають план дослідження функції на зростання (спадання).(Слайд№11)

Приклад.
у = 0,2х5 - 4/3 х3
1. визначена при будь-якому х
2. у '= х4 - 4х2
3. у ' існує в усіх точках.
у '= 0; х4 - 4х2 = 0;
х2 (х - 2) (х + 2) = 0
4.



-2
2
0
+ – – + у ' у
у
5. Функція зростає х є (-∞; -2] і [2; + ∞). Функція спадає х є [-2; +2].
Відповідь: функція зростає х є (-∞; -2] і [2; + ∞), спадає х є [-2; +2].
Практика під керівництвом учителя.
Учні виконують завдання по порядку (кожен у своєму темпі), учитель перевіряє, дає рекомендації кожному індивідуально.
На «4-6» - №11.1 - 2 на вибір.
На «7-9» +№11.3(5-8) – 2 на вибір
На «10,11» + досліджувати функцію на монотонність
у = 0,25х4 - 2х3 + 5,5х2 - 6х + 2π
6. Д / з :§1, пункт 11. №11.2 (1,3), №11.7,№11.11.
7. Підсумок уроку .











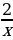 ; б)у = х2 - 6;в) у = - х2 + 4х +6; г)у = 0,2х5 -
; б)у = х2 - 6;в) у = - х2 + 4х +6; г)у = 0,2х5 - 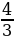 х3
х3






















 у
у 










