Теорема Карно и её приложения

Муниципальное автономное общеобразовательное учреждение "Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина"

ИНДИВИДУАЛЬНЫЙ ПРОЕКТ

по теме:

«Теорема Карно»

Выполнил:

Учащийся 10 класса «К»

Ковешников Олег Александрович

Научный руководитель:

Козадаев Виктор Сергеевич

Тамбов, 2016

Оглавление

Введение 3

Основная часть 4

Глава 1. Биография Лазара Карно 4

Глава 2. Формулировка теоремы Карно 5

Глава 3. Доказательство теоремы Карно 6

Глава 4. Примеры решения задач 8

Заключение 11

Список литературы 12

Введение

Моя работа посвящена исследованию в области геометрии треугольника, а в частности малоизвестной, но очень полезной теоремы Карно. Данная теорема не изучается в школах, чем и вызывает неподдельный интерес.

Актуальность этой темы состоит в том, что теорема Карно может оказаться единственным ключом к правильному ответу сложнейших олимпиадных задач.

Цель проекта: тщательно изучить теорему Карно и все, что с ней связано путем изучения и анализа большого количества научной информации. Для достижения этой цели необходимо выделить основные этапы исследования – задачи.

Задачи проекта:

1. познакомиться с биографией Лазара Карно – автора теоремы.

2. доказать теорему

3. решить несколько задач с помощью теоремы Карно.

Основная часть

Глава 1. Биография Лазара Карно

Родился Лазар Карно в 1753. Он окончил военную школу и поступил на службу в инженерные войска. Где кроме, собственно, службы, писал научные статьи и даже стихи. Позже в 1791 он стал депутатом Законодательного собрания Франции, но Карно посвятил себя военному делу. После успешной организации обороны на границе Восточных Пиренеев, Карно был назначен членом Комитета Общественного Спасения. Именно он организовал оборону по всей границе государства и руководил военными действиями во время войны с Австрией. За свою деятельность Карно получил прозвание “организатора победы”.

Вместе с Наполеоном 1795 году Лазар уже в качестве члена Директории разработал план похода в Италию. Но пробыл он на новой должности совсем недолго. Уже в 1797 в ходе разногласий в Директории против Карно затеяли заговор, но вовремя предупрежденный он бежал в Швейцарию, откуда позже переехал в Южную Германию.

Что касается наиболее интересной, т.е. научной стороны его жизни, то как ученый Карно больше всего увлекался математическим анализом и геометрией. Но также несколько его трудов посвящены паровым машинам и механическим устройствам. Еще в 1797, будучи членом директории Карно издал свои «Размышления о метафизике исчисления бесконечно малых». Потом он издал ряд научных трудов, которые он предоставил институту, в основании которого он принимал дельное участие. Среди них были очень важные монографии, такие как «О соотношении геометрических фигур» и «Геометрия положения», где он впервые изложил и доказал свою теорему, позже названной теоремой Карно, о которой речь пойдет в следующих разделах. В математическом анализе его больше всего интересовали вопрос надобности комплексных чисел и разбор различных способов обоснования анализа, он резко критиковал теорию аналитических функций, что стало предпосылкой реформы анализа. Также Карно приложил немало усилий, чтобы достичь максимального КПД двигателя автомобиля, его исследования в этой области продолжил его сын, Сади Карно, предложивший цикл с теоретически максимальным КПД, названный в его честь.

В 1815 году правительство издало указ об изгнании Карно за поддержку Наполеона, и он провел последние годы своей жизни в маленьком городке, Магдебурге. Здесь он успел издать еще несколько сочинений, и возрасте семидесяти лет скончался в 1823 году. Позже его тело было перевезено во Францию и заново погребено в Пантеоне.

Глава 2. Формулировка теоремы Карно

В связи с тем, что на счету у Карно несколько теорем названных его именем, то данную теорему часто называют формулой Карно или японской теоремой Карно.

Теорема Карно: Сумма расстояний от центра описанной окружности до сторон остроугольного треугольника равняется сумме радиусов описанной и вписанной окружностей.

Важно заметить, что данная формулировка теоремы подходит только для остроугольного треугольника, но это не значит, что в тупоугольном и прямоугольном треугольниках она не применима. Тогда расстояние от центра описанной окружности до стороны, лежащей против тупого угла берется со знаком минус.

Приведем пример:

Пусть D – центр описанной окружности треугольника ABC, тогда

сумма расстояний от точки D до сторон треугольника, взятых со знаком “-”, если отрезок полностью лежит за пределами треугольника, будет равно сумме радиусов описанной и вписанной окружности (Рис.1).

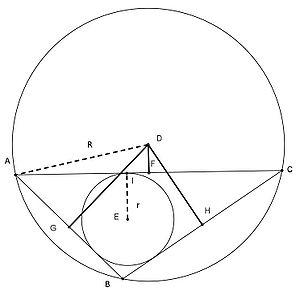
DG + DH – DF = R + r

Рис. 1

В прямоугольном треугольнике сумма расстояний от центра гипотенузы до катетов будет равно сумме радиусов описанной и вписанной окружности, так как центр описанной окружности лежит на гипотенузе поэтому одно из трех расстояний равно нулю.

Глава 3. Доказательство теоремы Карно

Рассмотрим окружность, описанную около треугольника ABC. Пусть он будет остроугольным, биссектриса угла А пересекает окружность в точке W, а D ей диаметрально противоположна.

Доказательство будем проводить в несколько этапов. Сначала докажем два вспомогательных факта:

1) M₁W = ( r_a - r ) / 2;

2) M₁D = ( r_b + r_c ) / 2, где r, r_{a ,} r_b , r_c радиусы вписанной окружности и вневписанных окружностей, касающихся сторон BC, AC и AB соответственно.

Докажем, что M₁W = ( r_a - r ) / 2

П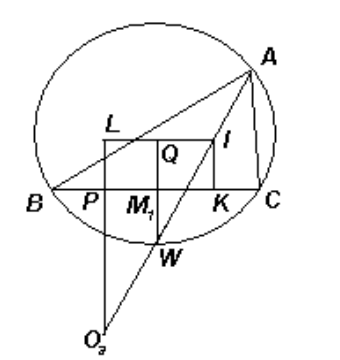усть I – центр вписанной в треугольник окружности, касающейся BC в точке K, Q_a – центр вневписанной окружности, касающейся стороны BC в точке P, а M₁ – точка, в которой перпендикуляр из центра описанной окружности около треугольника ABC пересекает сторону BC, т.е. M₁B= M₁C(Рис.2).

Т

Рис. 2

.к. AW – биссектриса, то по теореме трилистника BW=CW=IW=WQ_a, следовательно, треугольник BWC – равнобедренный и, т.к. M₁B= M₁C, WM₁ – высота в треугольнике BWC т.е. WM₁⊥BC. Теперь проведем прямую параллельную прямой BC через точку I и опустим на нее перпендикуляр из Q_a, пересекающий прямую в точке L. Т.к. Q_aL перпендикулярна IL и, следовательно, перпендикулярна и прямой BC, и WM₁⊥BC, то Q_aL||WM₁. Из теоремы трилистника IW=WQ_a. Продолжим отрезок WM₁ до пересечения с IL и обозначим точку пересечения за Q. Получаем, что QW – средняя линия в треугольнике ILQ_a. Следовательно, QW=LQ_a/2. По теореме Фалеса, из того, что QW||IK (т.к. QW⊥BC и IK⊥BC) и IL||BC, следует, что WM₁= LQ_a/2-IK. Распишем LQ_a как сумму Q_aP + IK (IK=PL по теореме Фалеса). Заметим, что Q_aP – радиус вневписанной окружности, касающейся стороны BC, а IK – радиус вписанной окружности. В итоге получаем: WM₁= LQ_a/2-IK=(r_a+r) /2-r=(r_a-r) /2 – первый пункт доказан.

Отметим важный факт, что точки касания вписанной и вневписанной окружностей к одной стороне симметричны относительно центра стороны (PM₁=M₁K по теореме Фалеса т.к. IW=WQ_a и Q_aL||WQ||IK). А, следовательно, и расстояния от точек касания до ближайших вершин равны(BP=KC) Знание этого свойства пригодится нам в доказательстве второго пункта, к которому мы сейчас же и приступим.

Докажем, что M₁D = ( r_b + r_c ) / 2.

Если WD – диаметр, то ∠DAW=90 градусов, следовательно, биссектрисы внешних углов при вершине A лежат на прямой AD (Рис. 3). На этих биссектрисах лежат центры вневписанных окружностей Q_c(касающаяся AB) и Q_b(касающаяся AC). Опустим перпендикуляры Q_cB₀ и Q_bС₀ на прямую BC. Пусть T – точка касания вневписанной окружности с центром Q_с стороны AB. Тогда по свойству касательных B₀B=BT. Пусть N – точка касания стороны AB вписанной окружности, тогда BT=AN, т.к. расстояния от точек касания вневписанной и описанной окружностей к одной стороне до ближайших вершин равны. Аналогично и со стороной AC. В итоге получаем, что BB₀=CC₀ и мы знаем, что M₁B=M₁C, следовательно, B₀M₁=M₁C₀, получается, что DW₁ – средняя линия в трапеции B₀Q_cQ_bC₀(B₀Q_c||Q_bC₀) и равна (B₀Q_c+Q_bC₀)/2, где B₀Q_c=r_c, а Q_bC₀=r_b. Получаем, что M₁D=(r_b+r_c)/2.

D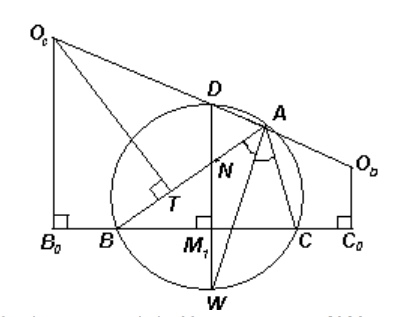M₁+M₁W=DW=2R

П

Рис. 3

одставляем значения DM₁ и M₁W. Получаем, что 4R+r=r_a+r_b+r_c. Теперь распишем каждое из расстояний от центра описанной окружности до сторон.

OM₁=R - ( r_a - r ) / 2

OM₂=R - ( r_b - r ) / 2

OM₃=R - ( r_c - r ) / 2

Складываем все уравнения и получаем:

OM₁+OM₂+OM₃=(6R-r_a-r_b-r_c+3r)/2, вместо r_a+r_b+r_c подставляем 4R+r и получаем окончательный ответ.

OM₁+OM₂+OM₃=R+r – сумма расстояний от центра описанной окружности до сторон остроугольного треугольника является величиной постоянной и равняется сумме радиусов описанной и вписанной окружностей.

Но изначально мы сказали, что треугольник ABC остроугольный.

Р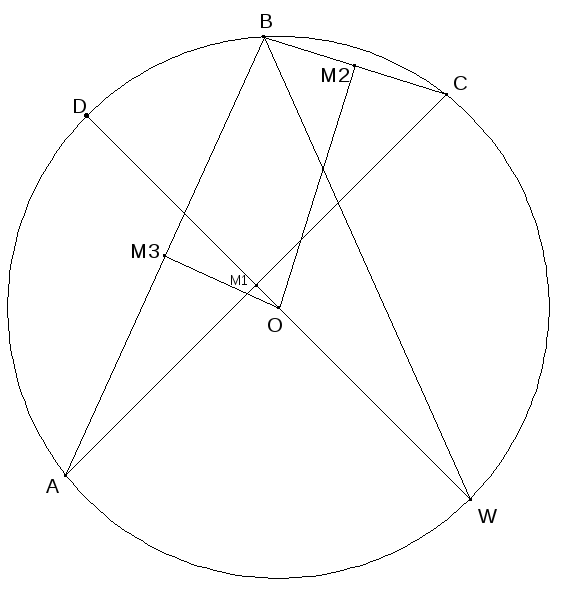ассмотрим тот случай, когда треугольник тупоугольный, а именно когда расстояние от центра описанной окружности находится вне треугольника (Рис. 4).

Расстояния DM₁ и WM₁ также, как и у остроугольного треугольника, равны ( r_b + r_c ) /2 и ( r_a - r ) /2 соответственно.

Но расстояние OM₁ равно, не R-WM₁, а WM₁-R.

Остальные расстояния от центра описанной окружности остаются неизменными.

OM₁=( r_a - r ) / 2-R.

OM₂=R - ( r_b - r ) / 2

OM₃=R - ( r_c - r ) / 2

Н

Рис. 4

айдем сумму OM₃+OM₂-OM₁:

OM₃+OM₂-OM₁=(6R-r_a-r_b-r_c+3r)/2=R+r

Теорема доказана.

Глава 4. Примеры решения задач

Задача 1: Четырехугольник ABCD вписан в окружность с центром в точке О. Доказать, что r₁+r₂=r₃+r₄, где r₁ ,r₂ ,r₃ и r₄ – радиусы вписанных окружностей в треугольники ABC, ADC, ABD и BCD соответственно.

Доказательство:

Пусть имеем четырехугольник ABCD, вписанный в окружность с центром в точке О (Рис. 5). Тогда применим теорему Карно к каждому из треугольников ABC, ADC, ABD и BCD. Естественно радиус описанной окружности у данных треугольников одинаковый и равен радиусу описанной окружности около четырехугольника ABCD.

Д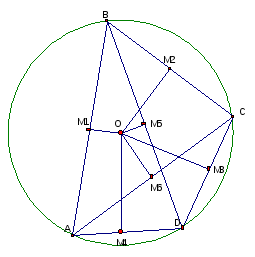ля треугольника ABC:

OM₁+OM₂+OM₆=R+r₁ (1)

Для треугольника ADC:

OM₃+OM₄-OM₆=R+r₂ (2)

Для треугольника ABD:

OM₁+OM₄+OM₅=R+r₃ (3)

Для треугольника BCD:

OM₂+OM₃-OM₅=R+r₄ (4)

С

Рис. 5

ложим уравнения (1) с (2) и (3) с (4). Получим:

OM₁+OM₂+ OM₃+OM₄=2R+r₂+r₁

OM₁+OM₂+ OM₃+OM₄=2R+r₃+r₄

Левые части двух полученных уравнений равны, следовательно, равны и правые части.

2R+r₂+r₁=2R+r₃+r₄

Отсюда и следует, что r₁+r₂=r₃+r₄

Задача 2: Доказать, что сумма расстояний от вершин остроугольного треугольника до его ортоцентра (точки пересечения высот) равняется сумм е диаметров вписанной и описанной окружностей.

Доказательство:

К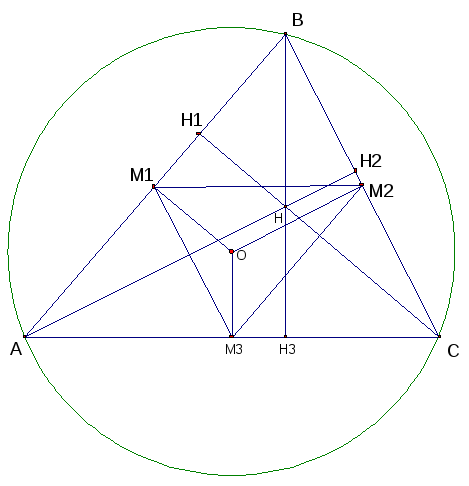

Рис. 6

ак известно, центр описанной окружности является ортоцентром треугольника, вершины которого лежат на серединах сторон данного треугольника. Т.е. в треугольнике M₁M₂M₃ O – точка пересечения высот, коими являются прямые OM₁,OM₂ и OM₃(Рис. 6). ΔM₁M₂M₃ подобен ΔABC(т.к. каждая сторона в ΔM₁M₂M₃ является средней линией ΔABC, и поэтому отношения сторон треугольника M₁M₂M₃ к соответственным сторонам треугольника ABC равняется ½). Раз эти треугольники подобны, то все линейные элементы в треугольниках относятся как ½, в том числе и расстояния от вершин до ортоцентра. Следовательно, сумма расстояний также будет относится, как 1 к 2.

В ΔM₁M₂M₃ сумма расстояний от вершин до ортоцентра равна OM₁+OM₂+ OM₃, а в ΔABC OM₁,OM₂ и OM₃ – расстояния от центра описанной окружности до сторон треугольника, применив теорему Карно, получаем: OM₁+OM₂+OM₃=R+r, тогда сумма расстояний от вершин до ортоцентра в ΔABC в два раза больше. В итоге:

HH₁+HH₂+HH₃=2(OM₁+OM₂+ OM₃)

HH₁+HH₂+HH₃=2(R+r)=D+d

Получили, что сумма расстояний от вершины до ортоцентра равно сумме диаметров описанной и вписанной окружностей, что и требовалось доказать.

Задача 3: Докажите неравенство Эрдеша(h=R+r), где h – наибольшая высота в треугольнике, а R и r радиусы описанной и вписанной окружностей.

Д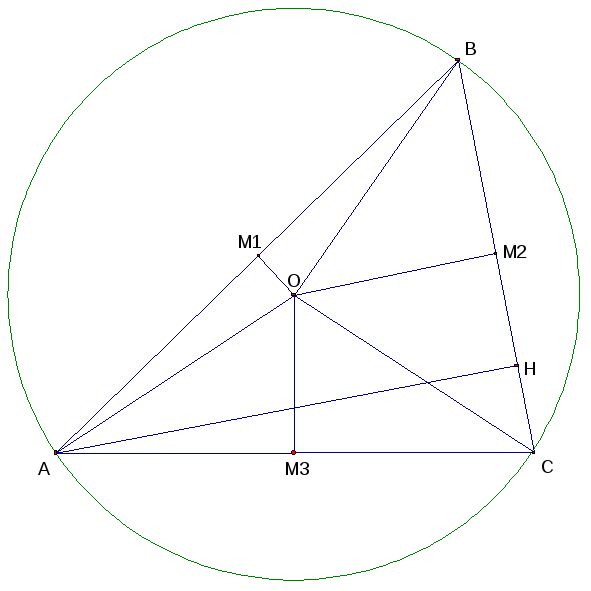оказательство:

Пусть имеем ΔABC. Положим для определенности, что BC – наименьшая сторона, а ΔABC остроугольный. Тогда высота, проведенная к ней(AH) будет наибольшей (Рис. 7).

Применим теорему Карно к ΔABC:

OM₁+OM₂+ OM₃=R+r

Умножим обе части уравнения на BC. Получим:

BC·OM₁+BC·OM₂+BC·OM₃=BC(R+r)

С

Рис. 7

равним сумму в левой части уравнения с площадью треугольника ABC:

S=S_AOB+S_AOC+S_BOC=½(AB·OM₁+BC·OM₂+AC·OM₃)

S=½(AB·OM₁+BC·OM₂+AC·OM₃)

Если мы заменим AB и AC в этом уравнении на BC, то сумма в правой части уменьшится (BC – наименьшая сторона). Получим неравенство:

S½(BC·OM₁+BC·OM₂+BC·OM₃)=½ ·BC(R+r)

Распишем площадь как произведение высоты AH и основания BC, деленное пополам

AH·BC/2BC(R+r)/2

Делим обе части неравенства на BC/2, в итоге AHR+r.

Но изначально мы сказали, что в треугольнике есть наименьшая сторона, а если ее нет, т.е. все стороны равны, то тогда неравенство заменится на равенство.

Если ΔABC тупоугольный, то доказательство аналогично данному (Рис. 8)

По теореме Карно: OM₂+OM₃-OM₁=R+r

И S=S_AOC+S_BOC- S_AOB=½(BC·OM₂+AC·OM₃-AB·OM₁)

З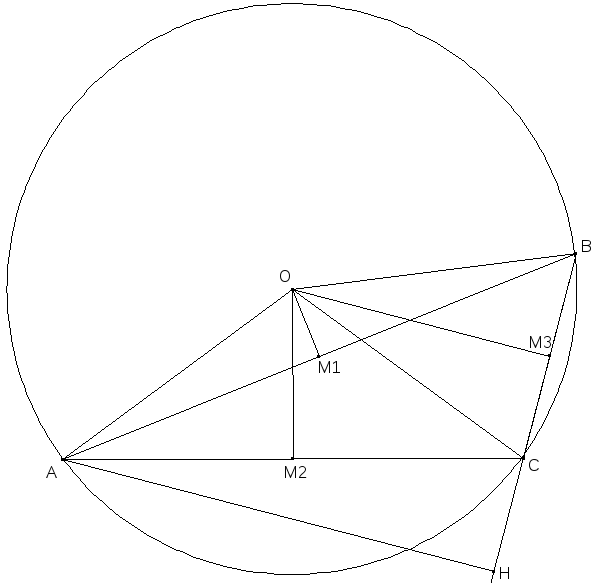аменив AB и AC на BC, получим неравенство

S=AH·BC/2BC(OM₂+OM₃-OM₁)/2. Следовательно, AHR+r. Естественно в тупоугольнике равенства не может быть, т.к. оно достигается только в том случае когда все стороны равны.

П

Рис. 8

олучили, что длина наибольшей высоты, больше либо равна сумме радиусов описанной и вписанной окружностей треугольника, что и требовалось доказать.

З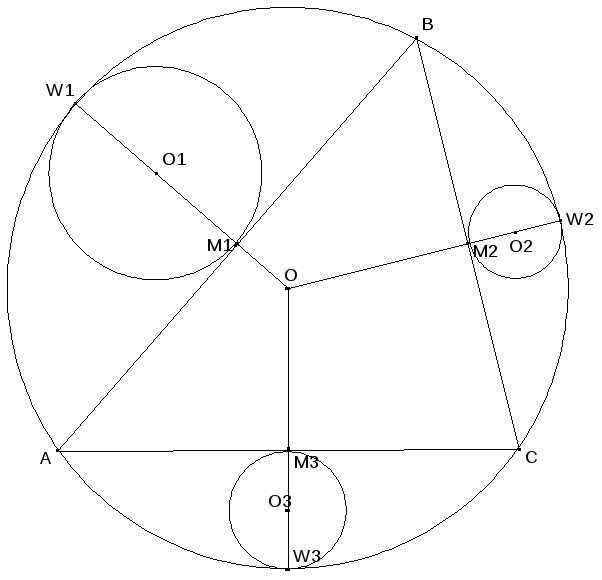адача 4: В окружность радиуса R вписан треугольник, а в каждый сегмент, ограниченный стороной треугольника и меньшей из дуг окружности, вписана окружность наибольшего радиуса. Найдите сумму диаметров трех получившихся окружностей и радиуса окружности, вписанной в треугольник.

Решение:

Чтобы радиус окружностей, вписанных в данные сегменты, был максимальным, то центр этих окружностей лежит на серединных перпендикулярах треугольника. W₁,W₂ и W₃ - центры дуг ограниченных сторонами треугольника и точки касания вписанных окружностей с центрами в точках O₁,O₂ и O₃, с диаметрами d₁, d₂ и d₃ соответственно(Рис. 9).

П

Рис. 9

рименим теорему Карно к ΔABC (положим для определенности, что ΔABC остроугольный)

OM₁+OM₂+OM₃=R+r

Прибавим к обеим частям сумму диаметров d₁, d₂ и d₃

(OM₁+d₁)+(OM₂+d₂)+(OM₃+d₃)=R+r+d₁+d₂+d₃

(OM₁+d₁)=(OM₂+d₂)=(OM₃+d₃)=R

Получаем:

3R=R+r+d₁+d₂+d₃, т.е. r+d₁+d₂+d₃=2R

Если ΔABC – тупоугольный, то решение аналогично.

Заключение

Основная цель и задачи выполнены. Я в полной мере изучил теорему Карно как формулировку, так и два разных доказательства теоремы и научился ее применять, решая большое количество конкретных олимпиадных задач, но сюда попали только некоторые из них. В целом работа была не сложной, главная трудность заключалась в поиске и систематизации большого количества информации. И могу сказать, что справился с этим, и не только с этим, но и со всеми задачами проекта.

Список литературы

Блинков, А. Д. Формула Карно [Электронный ресурс] / Блинков Александр Давидович //geometry.ru – М., 2010. – Режим доступа: http://geometry.ru/persons/blinkov/10/Karno_formula.pdf – 2010 г.

Формула Карно [Электронный ресурс] / – Режим доступа: www.url: https://ru.wikipedia.org/wiki/Формула_Карно – 2016 г.

Карно, Лазар [Электронный ресурс] / – Режим доступа: www.url: https://ru.wikipedia.org/wiki/Карно,_Лазар – 2016 г.

12