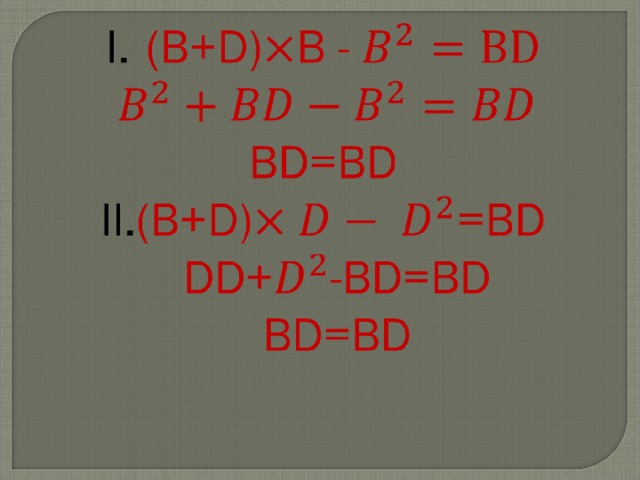Теорема Виета. Чернов Вадим

Творческий проект

«Теорема Виета»

выполнил: ученик 8Б класса

Чернов Вадим

Руководитель: учитель математики

Малкова Елена Михайловна

Г. Ульяновск

2016 г.

Цели:

• Узнать где применяется эта теорема.
• Изучить теорему Виета, ее доказательства, замечания, примеры.
• Вспомнить кто такой Франсуа Виет.

Где же применяется теорема Виета?

Часто требуется найти сумму квадратов  (x 1 2 +x 2 2 )  или сумму кубов (x 1 3 +x 2 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения. Помочь в этом может теорема Виета

Франсуа Виет (1540–1603) родился во Франции. Разработал почти всю элементарную алгебру; ввёл в алгебру буквенные обозначения и построил первое буквенное исчисление.

Историческая справка

• По образованию – юрист, много занимался адвокатской деятельностью. Но все свое свободное время, досуг отдавал занятиям математикой. Именно преподавание математики пробудило в молодом юристе интерес к ней. Виет детально изучал труды, как древних, так и современных ему математиков. Виет создал по существу новую алгебру. Он ввел в нее буквенную символику и показал, как, оперируя символами, можно получить результат, который применим к любым соответствующим величинам, т.е. решить задачу в его общем виде. Это положило начало коренному перелому в развитии алгебры: стало возможным буквенное исчисление.
• Демонстрируя силу своего метода, ученый привел в своих работах запас формул, которые могли быть использованы для решения конкретных задач.
• Действительно, мы знаем, как легко решать, например, квадратные уравнения. Для их решения имеются готовые формулы. До Ф.Виета решение квадратных уравнений выполнялось по своим правилам в виде очень длинных словесных рассуждений. После открытия Виета стало возможным записывать правила в виде формул.

По праву достойна в стихах быть воспета

О свойства корней теорема Виета

Что, лучше скажи постоянства такого

Умножить ты корни – и дробь уж готова

В числителе с в знаменателе а

А сумма корней тоже дроби равна

Хоть с минусом дробь, что за беда

В числители в в знаменателе а

Так выглядела изначально Теорема Виета.

Расшифруйте буквы и что они означали.

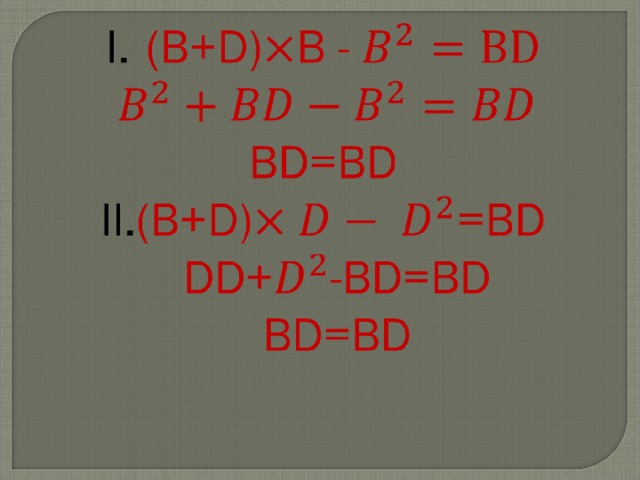
• Мы знаем, что при D ≥0 корни приведённого квадратного уравнения находятся по формуле

.

• Теперь выполним алгеб раические преобразования – и теорема Виета доказана:

.

• Ещё одно интересное соотношение – дискриминант уравнения равен квадрату разности его корней:

D=(x 1 -x 2 ) 2 .

Не используя формулу корней, найдите корни квадратного уравнения:

Ответы:

• -1; -2
• 14; 1
• -4;1
• 11;1

Ответы:

• 18;1
• -7;-1
• 10;-1
• -9;1